Some functions exhibit symmetry so that reflections result in the original graph. For example, horizontally reflecting the toolkit functions [latex]f\left(x\right)={x}^{2}[/latex] or [latex]f\left(x\right)=|x|[/latex] will result in the original graph. We say that these types of graphs are symmetric about the y-axis. Functions whose graphs are symmetric about the y-axis are called even functions.
If the graphs of [latex]f\left(x\right)={x}^{3}[/latex] or [latex]f\left(x\right)=\frac{1}{x}[/latex] were reflected over both axes, the result would be the original graph.
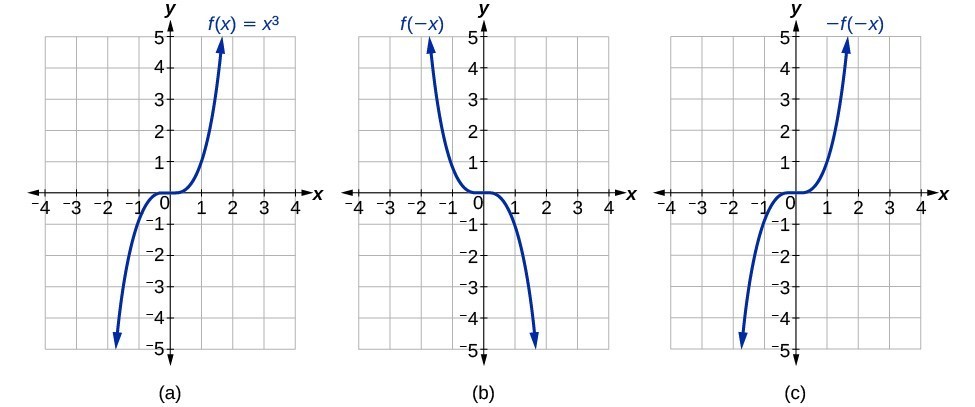
Figure 12. (a) The cubic toolkit function (b) Horizontal reflection of the cubic toolkit function (c) Horizontal and vertical reflections reproduce the original cubic function.
We say that these graphs are symmetric about the origin. A function with a graph that is symmetric about the origin is called an odd function.
Note: A function can be neither even nor odd if it does not exhibit either symmetry. For example, [latex]f\left(x\right)={2}^{x}[/latex] is neither even nor odd. Also, the only function that is both even and odd is the constant function [latex]f\left(x\right)=0[/latex].
A General Note: Even and Odd Functions
A function is called an even function if for every input [latex]x[/latex]
The graph of an even function is symmetric about the [latex]y\text{-}[/latex] axis.
A function is called an odd function if for every input [latex]x[/latex]
The graph of an odd function is symmetric about the origin.
How To: Given the formula for a function, determine if the function is even, odd, or neither.
- Determine whether the function satisfies [latex]f\left(x\right)=f\left(-x\right)[/latex]. If it does, it is even.
- Determine whether the function satisfies [latex]f\left(x\right)=-f\left(-x\right)[/latex]. If it does, it is odd.
- If the function does not satisfy either rule, it is neither even nor odd.
Example 9: Determining whether a Function Is Even, Odd, or Neither
Is the function [latex]f\left(x\right)={x}^{3}+2x[/latex] even, odd, or neither?
Solution
Without looking at a graph, we can determine whether the function is even or odd by finding formulas for the reflections and determining if they return us to the original function. Let’s begin with the rule for even functions.
This does not return us to the original function, so this function is not even. We can now test the rule for odd functions.
Because [latex]-f\left(-x\right)=f\left(x\right)[/latex], this is an odd function.
Try It 4
Is the function [latex]f\left(s\right)={s}^{4}+3{s}^{2}+7[/latex] even, odd, or neither?
Candela Citations
- Precalculus. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175. License: CC BY: Attribution. License Terms: Download For Free at : http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175.
- Introduction to Odd and Even Functions. Authored by: Mathispower4u. Located at: https://www.youtube.com/watch?v=VvUI6E78cN4. License: All Rights Reserved. License Terms: Standard YouTube License
Analysis of the Solution
Consider the graph of [latex]f[/latex]. Notice that the graph is symmetric about the origin. For every point [latex]\left(x,y\right)[/latex] on the graph, the corresponding point [latex]\left(-x,-y\right)[/latex] is also on the graph. For example, (1, 3) is on the graph of [latex]f[/latex], and the corresponding point [latex]\left(-1,-3\right)[/latex] is also on the graph.
Figure 13