Any conic may be determined by three characteristics: a single focus, a fixed line called the directrix, and the ratio of the distances of each to a point on the graph. Consider the parabola [latex]x=2+{y}^{2}[/latex] shown in Figure 2.
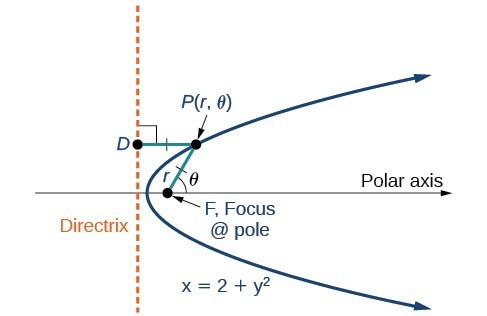
Figure 2
In The Parabola, we learned how a parabola is defined by the focus (a fixed point) and the directrix (a fixed line). In this section, we will learn how to define any conic in the polar coordinate system in terms of a fixed point, the focus [latex]P\left(r,\theta \right)[/latex] at the pole, and a line, the directrix, which is perpendicular to the polar axis.
If [latex]F[/latex] is a fixed point, the focus, and [latex]D[/latex] is a fixed line, the directrix, then we can let [latex]e[/latex] be a fixed positive number, called the eccentricity, which we can define as the ratio of the distances from a point on the graph to the focus and the point on the graph to the directrix. Then the set of all points [latex]P[/latex] such that [latex]e=\frac{PF}{PD}[/latex] is a conic. In other words, we can define a conic as the set of all points [latex]P[/latex] with the property that the ratio of the distance from [latex]P[/latex] to [latex]F[/latex] to the distance from [latex]P[/latex] to [latex]D[/latex] is equal to the constant [latex]e[/latex].
For a conic with eccentricity [latex]e[/latex],
- if [latex]0\le e<1[/latex], the conic is an ellipse
- if [latex]e=1[/latex], the conic is a parabola
- if [latex]e>1[/latex], the conic is an hyperbola
With this definition, we may now define a conic in terms of the directrix, [latex]x=\pm p[/latex], the eccentricity [latex]e[/latex], and the angle [latex]\theta[/latex]. Thus, each conic may be written as a polar equation, an equation written in terms of [latex]r[/latex] and [latex]\theta[/latex].
A General Note: The Polar Equation for a Conic
For a conic with a focus at the origin, if the directrix is [latex]x=\pm p[/latex], where [latex]p[/latex] is a positive real number, and the eccentricity is a positive real number [latex]e[/latex], the conic has a polar equation
For a conic with a focus at the origin, if the directrix is [latex]y=\pm p[/latex], where [latex]p[/latex] is a positive real number, and the eccentricity is a positive real number [latex]e[/latex], the conic has a polar equation
How To: Given the polar equation for a conic, identify the type of conic, the directrix, and the eccentricity.
- Multiply the numerator and denominator by the reciprocal of the constant in the denominator to rewrite the equation in standard form.
- Identify the eccentricity [latex]e[/latex] as the coefficient of the trigonometric function in the denominator.
- Compare [latex]e[/latex] with 1 to determine the shape of the conic.
- Determine the directrix as [latex]x=p[/latex] if cosine is in the denominator and [latex]y=p[/latex] if sine is in the denominator. Set [latex]ep[/latex] equal to the numerator in standard form to solve for [latex]x[/latex] or [latex]y[/latex].
Example 1: Identifying a Conic Given the Polar Form
For each of the following equations, identify the conic with focus at the origin, the directrix, and the eccentricity.
- [latex]r=\frac{6}{3+2\text{ }\sin \text{ }\theta }[/latex]
- [latex]r=\frac{12}{4+5\text{ }\cos \text{ }\theta }[/latex]
- [latex]r=\frac{7}{2 - 2\text{ }\sin \text{ }\theta }[/latex]
Solution
For each of the three conics, we will rewrite the equation in standard form. Standard form has a 1 as the constant in the denominator. Therefore, in all three parts, the first step will be to multiply the numerator and denominator by the reciprocal of the constant of the original equation, [latex]\frac{1}{c}[/latex], where [latex]c[/latex] is that constant.
- Multiply the numerator and denominator by [latex]\frac{1}{3}[/latex].
[latex]r=\frac{6}{3+2\sin \text{ }\theta }\cdot \frac{\left(\frac{1}{3}\right)}{\left(\frac{1}{3}\right)}=\frac{6\left(\frac{1}{3}\right)}{3\left(\frac{1}{3}\right)+2\left(\frac{1}{3}\right)\sin \text{ }\theta }=\frac{2}{1+\frac{2}{3}\text{ }\sin \text{ }\theta }[/latex]
Because [latex]\sin \text{ }\theta[/latex] is in the denominator, the directrix is [latex]y=p[/latex]. Comparing to standard form, note that [latex]e=\frac{2}{3}[/latex]. Therefore, from the numerator,
[latex]\begin{array}{l}\text{ }2=ep\hfill \\ \text{ }2=\frac{2}{3}p\hfill \\ \left(\frac{3}{2}\right)2=\left(\frac{3}{2}\right)\frac{2}{3}p\hfill \\ \text{ }3=p\hfill \end{array}[/latex]Since [latex]e<1[/latex], the conic is an ellipse. The eccentricity is [latex]e=\frac{2}{3}[/latex] and the directrix is [latex]y=3[/latex].
- Multiply the numerator and denominator by [latex]\frac{1}{4}[/latex].
[latex]\begin{array}{l}\begin{array}{l}\hfill \\ \hfill \\ r=\frac{12}{4+5\text{ }\cos \text{ }\theta }\cdot \frac{\left(\frac{1}{4}\right)}{\left(\frac{1}{4}\right)}\hfill \end{array}\hfill \\ r=\frac{12\left(\frac{1}{4}\right)}{4\left(\frac{1}{4}\right)+5\left(\frac{1}{4}\right)\cos \text{ }\theta }\hfill \\ r=\frac{3}{1+\frac{5}{4}\text{ }\cos \text{ }\theta }\hfill \end{array}[/latex]
Because [latex]\text{ cos}\theta[/latex] is in the denominator, the directrix is [latex]x=p[/latex]. Comparing to standard form, [latex]e=\frac{5}{4}[/latex]. Therefore, from the numerator,
[latex]\begin{array}{l}\text{ }3=ep\hfill \\ \text{ }3=\frac{5}{4}p\hfill \\ \left(\frac{4}{5}\right)3=\left(\frac{4}{5}\right)\frac{5}{4}p\hfill \\ \text{ }\frac{12}{5}=p\hfill \end{array}[/latex]Since [latex]e>1[/latex], the conic is a hyperbola. The eccentricity is [latex]e=\frac{5}{4}[/latex] and the directrix is [latex]x=\frac{12}{5}=2.4[/latex].
- Multiply the numerator and denominator by [latex]\frac{1}{2}[/latex].
[latex]\begin{array}{l}\hfill \\ \hfill \\ \begin{array}{l}r=\frac{7}{2 - 2\text{ }\sin \text{ }\theta }\cdot \frac{\left(\frac{1}{2}\right)}{\left(\frac{1}{2}\right)}\hfill \\ r=\frac{7\left(\frac{1}{2}\right)}{2\left(\frac{1}{2}\right)-2\left(\frac{1}{2}\right)\text{ }\sin \text{ }\theta }\hfill \\ r=\frac{\frac{7}{2}}{1-\sin \text{ }\theta }\hfill \end{array}\hfill \end{array}[/latex]
Because sine is in the denominator, the directrix is [latex]y=-p[/latex]. Comparing to standard form, [latex]e=1[/latex]. Therefore, from the numerator,
[latex]\begin{array}{l}\frac{7}{2}=ep\\ \frac{7}{2}=\left(1\right)p\\ \frac{7}{2}=p\end{array}[/latex]Because [latex]e=1[/latex], the conic is a parabola. The eccentricity is [latex]e=1[/latex] and the directrix is [latex]y=-\frac{7}{2}=-3.5[/latex].
Try It 1
Identify the conic with focus at the origin, the directrix, and the eccentricity for [latex]r=\frac{2}{3-\cos \text{ }\theta }[/latex].
Candela Citations
- Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175:1/Preface. License: CC BY: Attribution