Solutions

Solutions to Try Its

1. [−3,5]

2. (−∞,−2)∪[3,∞)

3. x<1 4. x≥−5 5. (2,∞) 6. [−314,∞) 7. [latex]6

Solutions to Odd-Numbered Exercises

1. When we divide both sides by a negative it changes the sign of both sides so the sense of the inequality sign changes.

3. (−∞,∞)

5. We start by finding the x-intercept, or where the function = 0. Once we have that point, which is (3,0), we graph to the right the straight line graph y=x−3, and then when we draw it to the left we plot positive y values, taking the absolute value of them.

7. (−∞,34]

9. [−132,∞)

11. (−∞,3)

13. (−∞,−373]

15. All real numbers (−∞,∞)

17. (−∞,−103)∪(4,∞)

19. (−∞,−4]∪[8,+∞)

21. No solution

23. (−5,11)

25. [6,12]

27. [−10,12]

29. x>−6 and x>−2Take the intersection of two sets.x>−2, (−2,+∞)

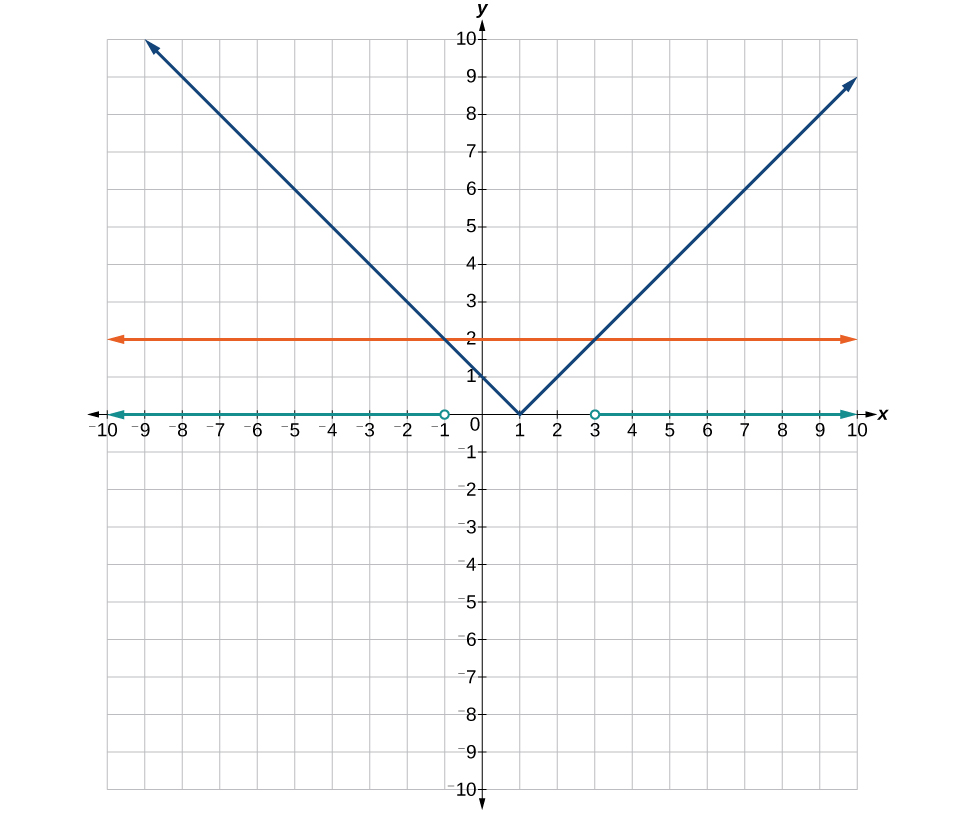
31. x<−3 or x≥1Take the union of the two sets.(−∞,−3)∪[1,∞) 33. (−∞,−1)∪(3,∞) A coordinate plane where the x and y axes both range from -10 to 10. The function |x 1| is graphed and labeled along with the line y = 2. Along the x-axis there is an open circle at the point -1 with an arrow extending leftward from it. Also along the x-axis is an open circle at the point 3 with an arrow extending rightward from it.

35. [−11,−3]
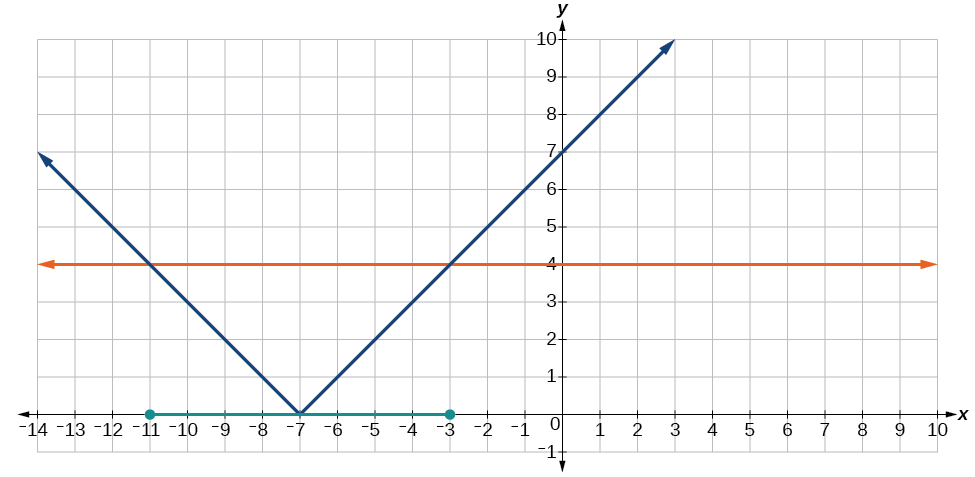
A coordinate plane with the x-axis ranging from -14 to 10 and the y-axis ranging from -1 to 10. The function y = |x + 7| and the line y = 4 are graphed. On the x-axis theres a dot on the points -11 and -3 with a line connecting them.

37. It is never less than zero. No solution.
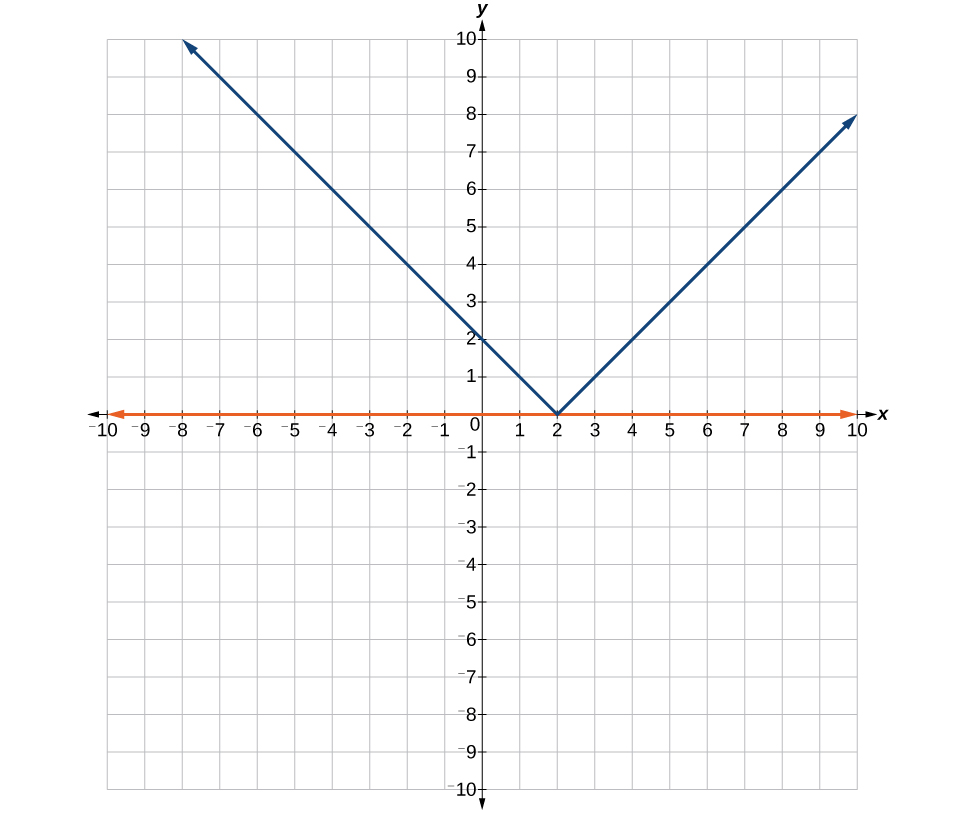
A coordinate plane with the x and y axes ranging from -10 to 10. The function y = |x -2| and the line y = 0 are graphed.

39. Where the blue line is above the orange line; point of intersection is x=−3.
(−∞,−3)
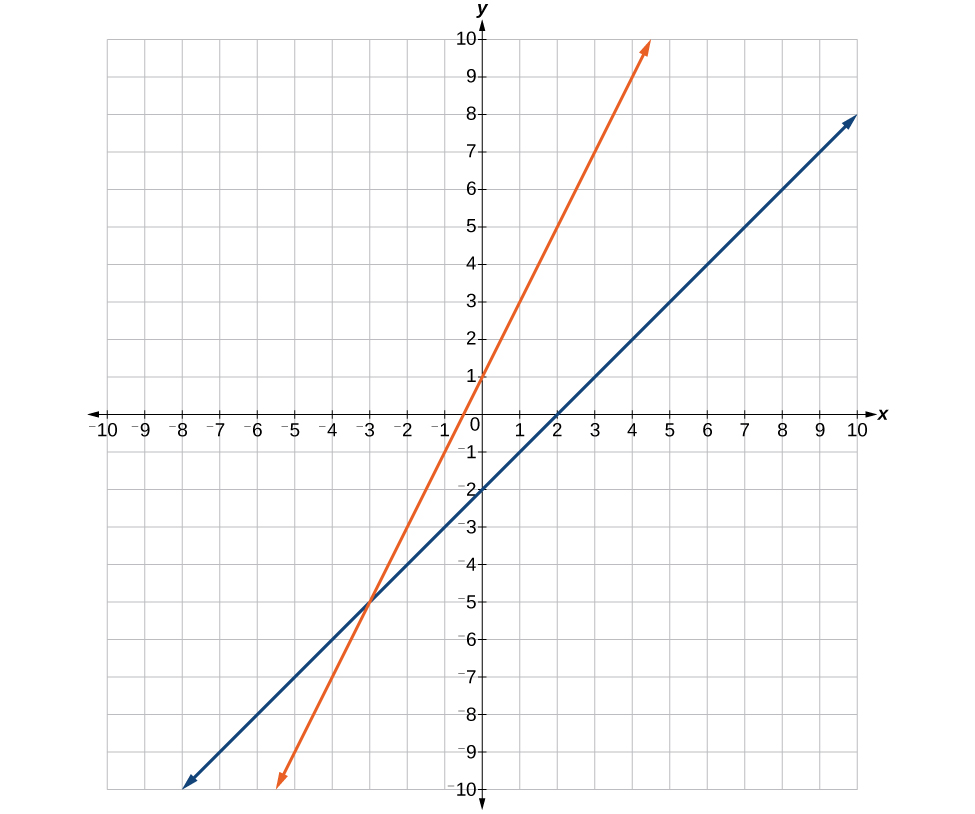
A coordinate plane with the x and y axes ranging from -10 to 10. The lines y = x - 2 and y = 2x + 1 are graphed on the same axes.

41. Where the blue line is above the orange line; always. All real numbers.
(−∞,−∞)
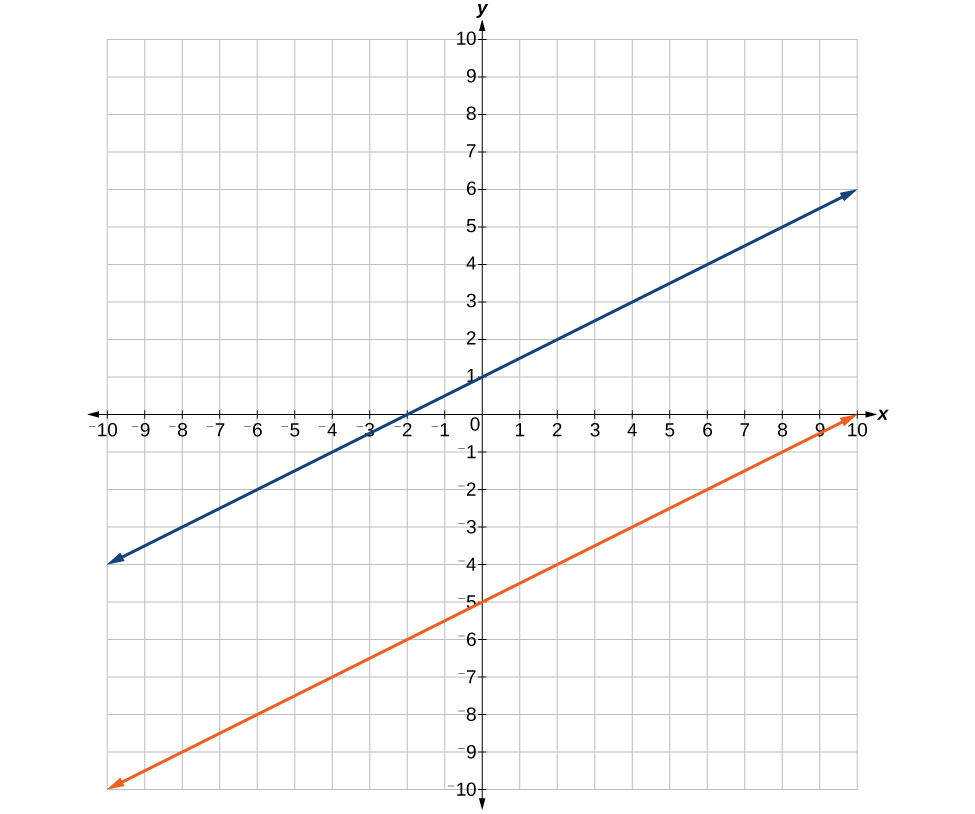
A coordinate plane with the x and y axes ranging from -10 to 10. The lines y = x/2 +1 and y = x/2 5 are both graphed on the same axes.

43. (−1,3)

45. (−∞,4)

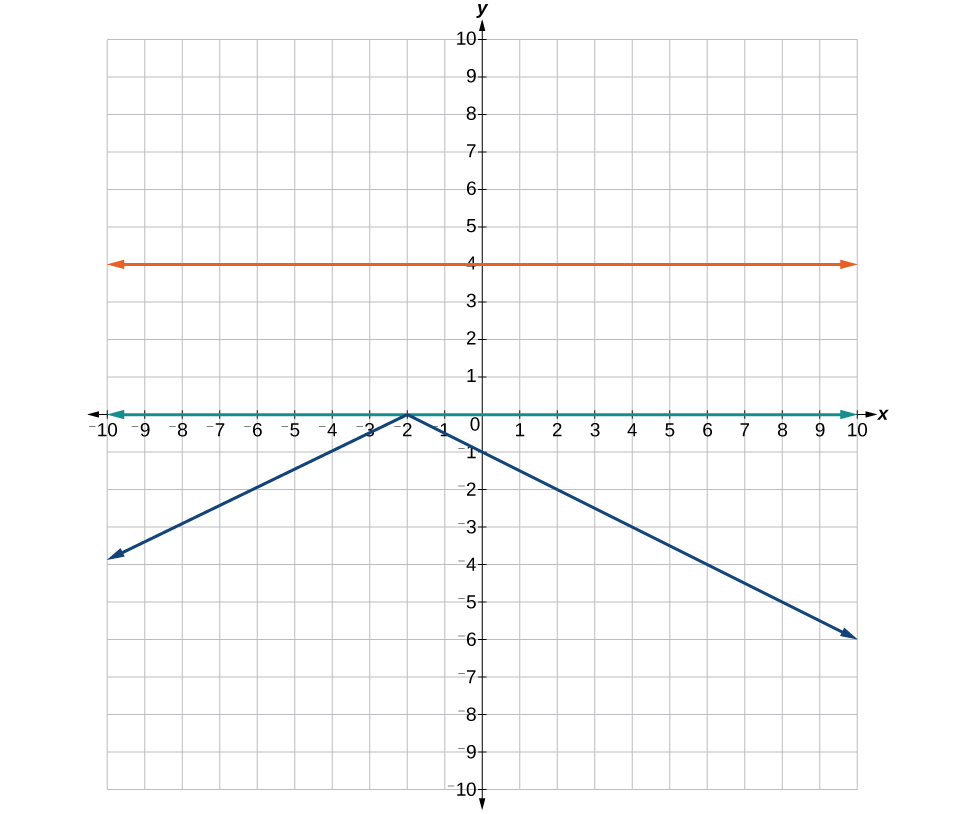
47. {x|x<6} 49. {x|−3≤x<5} 51. (−2,1] 53. (−∞,4] 55. Where the blue is below the orange; always. All real numbers. (−∞,+∞). A coordinate plane with the x and y axes ranging from -10 to 10. The function y = -0.5|x + 2| and the line y = 4 are graphed on the same axes. A line runs along the entire x-axis.

57. Where the blue is below the orange; (1,7).
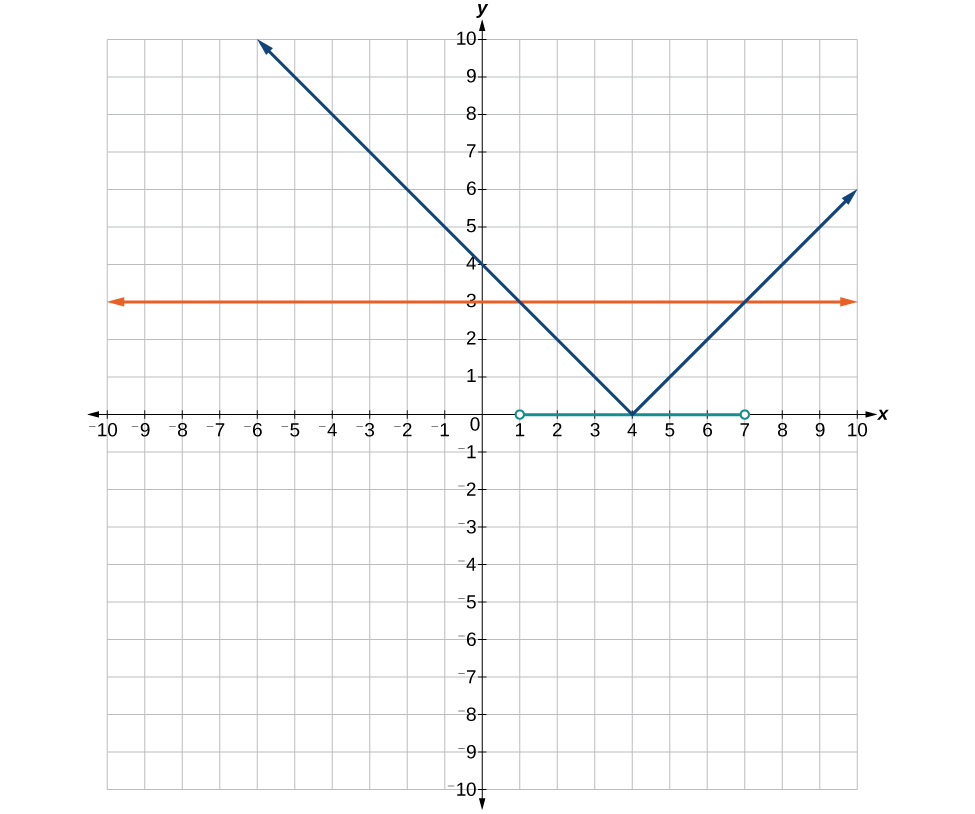
A coordinate plane with the x and y axes ranging from -10 to 10. The function y = |x 4| and the line y = 3 are graphed on the same axes. Along the x-axis the points 1 and 7 have an open circle around them and a line connects the two.

59. x=2,−45

61. (−7,5]

63. 80≤T≤1201,600≤20T≤2,400
[1,600,2,400]