Horizontal and Vertical Shifts of Logarithmic Functions

Learning Objectives

  • Graph horizontal and vertical shifts of logarithmic functions

As we mentioned in the beginning of the section, transformations of logarithmic graphs behave similarly to those of other parent functions. We can shift, stretch, compress, and reflect the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] without loss of shape.

Graphing a Horizontal Shift of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex]

When a constant c is added to the input of the parent function [latex]f\left(x\right)=\text{log}_{b}\left(x\right)[/latex], the result is a horizontal shift c units in the opposite direction of the sign on c. To visualize horizontal shifts, we can observe the general graph of the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] and for c > 0 alongside the shift left, [latex]g\left(x\right)={\mathrm{log}}_{b}\left(x+c\right)[/latex], and the shift right, [latex]h\left(x\right)={\mathrm{log}}_{b}\left(x-c\right)[/latex].

Try it

In the graphs below, you can use the slider for the variable c to investigate horizontal shifts that are produced by either adding or subtracting a constant from the input of a logarithmic function. The function [latex]f(x) = \log_{b}{x+c}[/latex] represents adding c units to the input of the function, and the function [latex]g(x) = \log_{b}{x-c}[/latex] represents subtracting c units from the input of the function.

Investigate the following questions:

  • Adjust the slider for c to 4.
  • Which direction does the graph of [latex]f(x)[/latex]shift? What is the vertical asymptote, x-intercept, and equation for this new function? How do the domain and range change?
  • Which direction does the graph of [latex]g(x)[/latex] shift? What is the vertical asymptote, x-intercept, and equation for this new function? How do the domain and range change?

https://www.desmos.com/calculator/6drjq3bh0m

The still graphs below summarize the changes in the x-intercepts, vertical asymptotes, and equations of a logarithmic function that has been shifted either right or left.

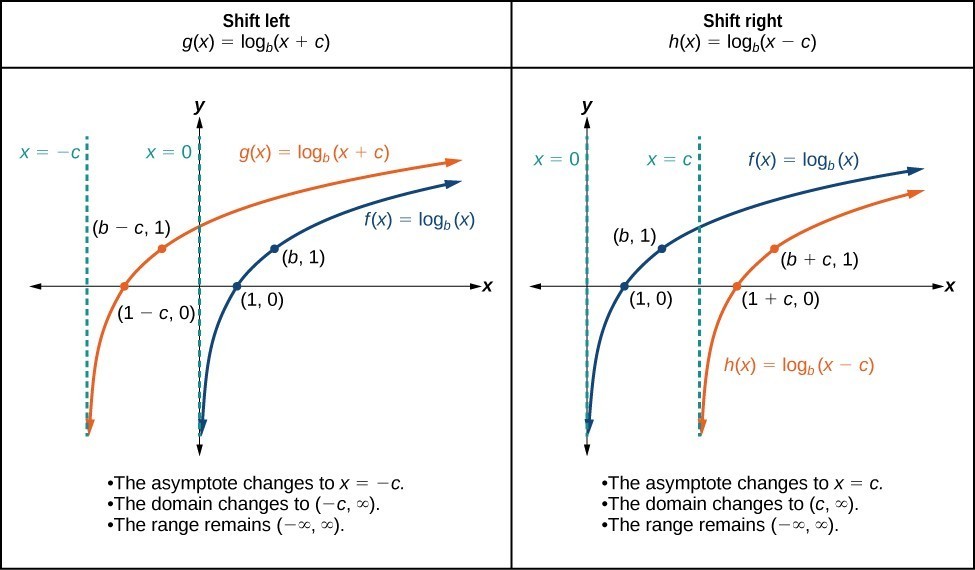
Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=log_b(x+c) is the translation function with an asymptote at x=-c. This shows the translation of shifting left.

A General Note: Horizontal Shifts of the Parent Function [latex]y=\text{log}_{b}\left(x\right)[/latex]

For any constant c, the function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x+c\right)[/latex]

  • shifts the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] left c units if c > 0.
  • shifts the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] right c units if c < 0.
  • has the vertical asymptote x = –c.
  • has domain [latex]\left(-c,\infty \right)[/latex].
  • has range [latex]\left(-\infty ,\infty \right)[/latex].

How To: Given a logarithmic function with the form [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x+c\right)[/latex], graph the translation.

  1. Identify the horizontal shift:
    1. If c > 0, shift the graph of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] left c units.
    2. If c < 0, shift the graph of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] right c units.
  2. Draw the vertical asymptote x = –c.
  3. Identify three key points from the parent function. Find new coordinates for the shifted functions by subtracting c from the x coordinate.
  4. Label the three points.
  5. The Domain is [latex]\left(-c,\infty \right)[/latex], the range is [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote is x = –c.

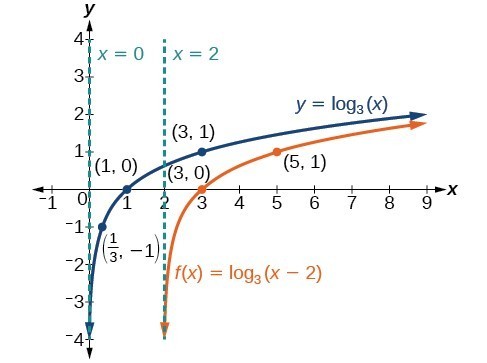
Example: Graphing a Horizontal Shift of the Parent Function [latex]y=\text{log}_{b}\left(x\right)[/latex]

Sketch the horizontal shift [latex]f\left(x\right)={\mathrm{log}}_{3}\left(x - 2\right)[/latex] alongside its parent function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.

Try It

Sketch a graph of [latex]f\left(x\right)={\mathrm{log}}_{3}\left(x+4\right)[/latex] alongside its parent function. Include the key points and asymptotes on the graph. State the domain, range, and asymptote.

Graphing a Vertical Shift of [latex]y=\text{log}_{b}\left(x\right)[/latex]

When a constant d is added to the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex], the result is a vertical shift d units in the direction of the sign on d. To visualize vertical shifts, we can observe the general graph of the parent function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] alongside the shift up, [latex]g\left(x\right)={\mathrm{log}}_{b}\left(x\right)+d[/latex] and the shift down, [latex]h\left(x\right)={\mathrm{log}}_{b}\left(x\right)-d[/latex].

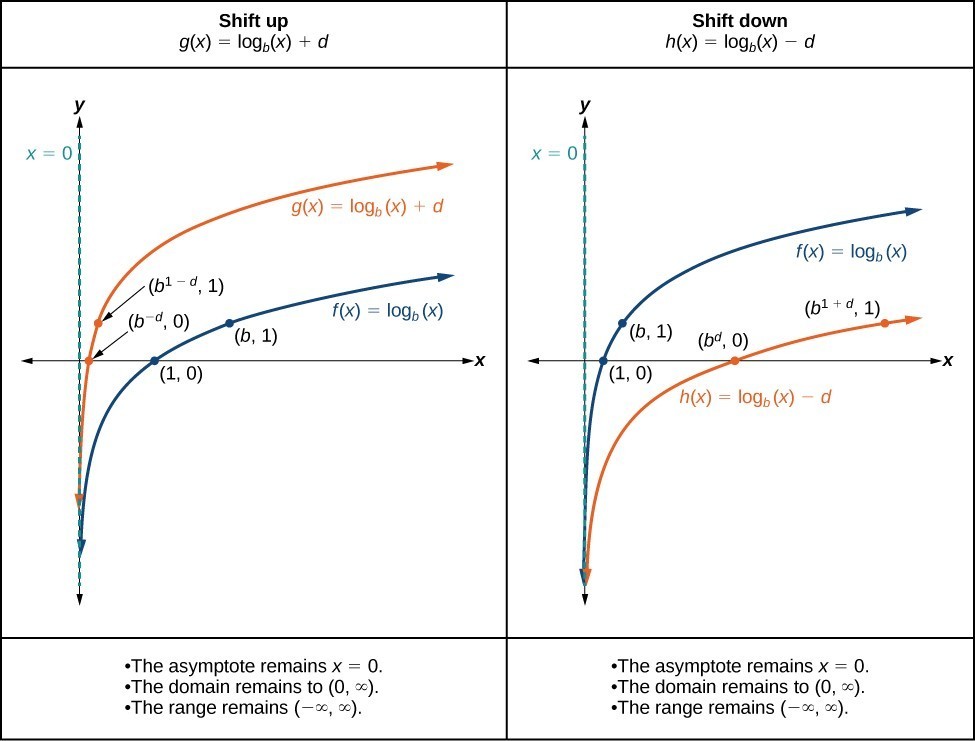
Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=log_b(x)+d is the translation function with an asymptote at x=0. This shows the translation of shifting up. Graph of two functions. The parent function is f(x)=log_b(x), with an asymptote at x=0 and g(x)=log_b(x)-d is the translation function with an asymptote at x=0. This shows the translation of shifting down.

A General Note: Vertical Shifts of the Parent Function [latex]y=\text{log}_{b}\left(x\right)[/latex]

For any constant d, the function [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)+d[/latex]

  • shifts the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] up d units if d > 0.
  • shifts the parent function [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] down d units if d < 0.
  • has the vertical asymptote x = 0.
  • has domain [latex]\left(0,\infty \right)[/latex].
  • has range [latex]\left(-\infty ,\infty \right)[/latex].

How To: Given a logarithmic function with the form [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)+d[/latex], graph the translation.

  1. Identify the vertical shift:
    1. If d > 0, shift the graph of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] up d units.
    2. If d < 0, shift the graph of [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] down d units.
  2. Draw the vertical asymptote x = 0.
  3. Identify three key points from the parent function. Find new coordinates for the shifted functions by adding d to the y coordinate.
  4. Label the three points.
  5. The domain is [latex]\left(0,\infty \right)[/latex], the range is [latex]\left(-\infty ,\infty \right)[/latex], and the vertical asymptote is x = 0.

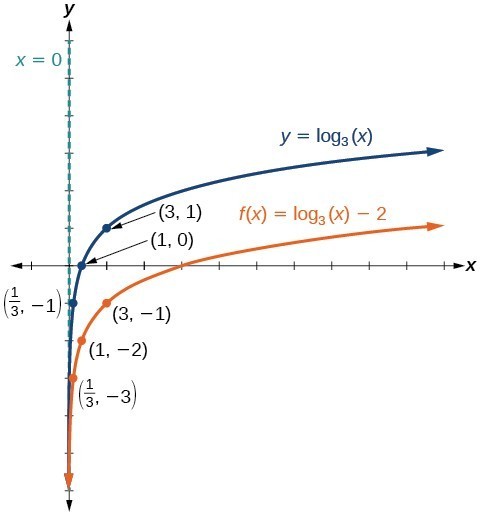
Example: Graphing a Vertical Shift of the Parent Function [latex]y=\text{log}_{b}\left(x\right)[/latex]

Sketch a graph of [latex]f\left(x\right)={\mathrm{log}}_{3}\left(x\right)-2[/latex] alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.

Try It

Sketch a graph of [latex]f\left(x\right)={\mathrm{log}}_{2}\left(x\right)+2[/latex] alongside its parent function. Include the key points and asymptote on the graph. State the domain, range, and asymptote.