Learning Outcomes
- Identify the base of an exponential function and restrictions for its value.
- Evaluate exponential functions.
- Evaluate exponential functions with base e.
- Investigate continuous growth and decay.
- Determine whether an exponential function and its associated graph represents growth or decay.
- Sketch a graph of an exponential function.
- Introduction to the logistic growth model
Focus in on a square centimeter of your skin. Look closer. Closer still. If you could look closely enough, you would see hundreds of thousands of microscopic organisms. They are bacteria, and they are not only on your skin, but in your mouth, nose, and even your intestines. In fact, the bacterial cells in your body at any given moment outnumber your own cells. But that is no reason to feel bad about yourself. While some bacteria can cause illness, many are healthy and even essential to the body.
An electron micrograph of E.Coli bacteria. (credit: “Mattosaurus,” Wikimedia Commons)
Bacteria commonly reproduce through a process called binary fission during which one bacterial cell splits into two. When conditions are right, bacteria can reproduce very quickly. Unlike humans and other complex organisms, the time required to form a new generation of bacteria is often a matter of minutes or hours as opposed to days or years.[1]
For simplicity’s sake, suppose we begin with a culture of one bacterial cell that can divide every hour. The table below shows the number of bacterial cells at the end of each subsequent hour. We see that the single bacterial cell leads to over one thousand bacterial cells in just ten hours! If we were to extrapolate the table to twenty-four hours, we would have over 16 million!
| Hour | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Bacteria | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
In this unit, we will explore exponential functions which can be used for, among other things, modeling growth patterns such as those found in bacteria. We will also investigate logarithmic functions which are closely related to exponential functions. Both types of functions have numerous real-world applications when it comes to modeling and interpreting data.
Evaluating Exponential Functions
The base of an exponential function must be a positive real number other than 1. Why do we limit the base b to positive values? This is done to ensure that the outputs will be real numbers. Observe what happens if the base is not positive:
- Consider a base of –9 and exponent of [latex]\frac{1}{2}[/latex]. Then [latex]f\left(x\right)=f\left(\frac{1}{2}\right)={\left(-9\right)}^{\frac{1}{2}}=\sqrt{-9}[/latex], which is not a real number.
Why do we limit the base to positive values other than 1? This is because a base of 1 results in the constant function. Observe what happens if the base is 1:
- Consider a base of 1. Then [latex]f\left(x\right)={1}^{x}=1[/latex] for any value of x.
To evaluate an exponential function with the form [latex]f\left(x\right)={b}^{x}[/latex], we simply substitute x with the given value, and calculate the resulting power. For example:
Let [latex]f\left(x\right)={2}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?
[latex]\begin{array}{llllllll}f\left(x\right)\hfill & ={2}^{x}\hfill & \hfill \\ f\left(3\right)\hfill & ={2}^{3}\text{}\hfill & \text{Substitute }x=3. \hfill \\ \hfill & =8\text{}\hfill & \text{Evaluate the power}\text{.}\hfill \end{array}[/latex]
To evaluate an exponential function, it is important to follow the order of operations. For example:
Let [latex]f\left(x\right)=30{\left(2\right)}^{x}[/latex]. What is [latex]f\left(3\right)[/latex]?
[latex]\begin{array}{c}f\left(x\right)\hfill & =30{\left(2\right)}^{x}\hfill & \hfill \\ f\left(3\right)\hfill & =30{\left(2\right)}^{3}\hfill & \text{Substitute }x=3.\hfill \\ \hfill & =30\left(8\right)\text{ }\hfill & \text{Simplify the power first}\text{.}\hfill \\ \hfill & =240\hfill & \text{Multiply}\text{.}\hfill \end{array}[/latex]
Note that if the order of operations were not followed, the result would be incorrect:
[latex]f\left(3\right)=30{\left(2\right)}^{3}\ne {60}^{3}=216,000[/latex]
Example: Evaluating Exponential Functions
Let [latex]f\left(x\right)=5{\left(3\right)}^{x+1}[/latex]. Evaluate [latex]f\left(2\right)[/latex] without using a calculator.
Try It
Let [latex]f\left(x\right)=8{\left(1.2\right)}^{x - 5}[/latex]. Evaluate [latex]f\left(3\right)[/latex] using a calculator. Round to four decimal places.
Because the output of exponential functions increases very rapidly, the term “exponential growth” is often used in everyday language to describe anything that grows or increases rapidly. However, exponential growth can be defined more precisely in a mathematical sense. If the growth rate is proportional to the amount present, the function models exponential growth.
A General Note: Exponential Growth
A function that models exponential growth grows by a rate proportional to the amount present. For any real number x and any positive real numbers a and b such that [latex]b\ne 1[/latex], an exponential growth function has the form
[latex]\text{ }f\left(x\right)=a{b}^{x}[/latex]
where
- a is the initial or starting value of the function.
- b is the growth factor or growth multiplier per unit x.
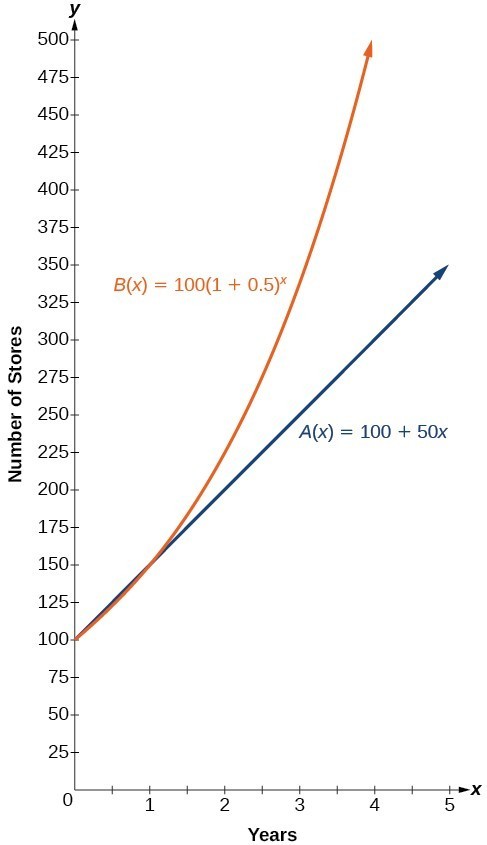
In more general terms, an exponential function consists of a constant base raised to a variable exponent. To differentiate between linear and exponential functions, let’s consider two companies, A and B. Company A has 100 stores and expands by opening 50 new stores a year, so its growth can be represented by the function [latex]A\left(x\right)=100+50x[/latex]. Company B has 100 stores and expands by increasing the number of stores by 50% each year, so its growth can be represented by the function [latex]B\left(x\right)=100{\left(1+0.5\right)}^{x}[/latex].
A few years of growth for these companies are illustrated below.
| Year, x | Stores, Company A | Stores, Company B |
|---|---|---|
| 0 | 100 + 50(0) = 100 | 100(1 + 0.5)0 = 100 |
| 1 | 100 + 50(1) = 150 | 100(1 + 0.5)1 = 150 |
| 2 | 100 + 50(2) = 200 | 100(1 + 0.5)2 = 225 |
| 3 | 100 + 50(3) = 250 | 100(1 + 0.5)3 = 337.5 |
| x | A(x) = 100 + 50x | B(x) = 100(1 + 0.5)x |
The graphs comparing the number of stores for each company over a five-year period are shown below. We can see that, with exponential growth, the number of stores increases much more rapidly than with linear growth.
The graph shows the numbers of stores Companies A and B opened over a five-year period.
Notice that the domain for both functions is [latex]\left[0,\infty \right)[/latex], and the range for both functions is [latex]\left[100,\infty \right)[/latex]. After year 1, Company B always has more stores than Company A.
Evaluating Exponential Functions with Base e
As n gets larger and larger, the expression [latex]{\left(1+\frac{1}{n}\right)}^{n}[/latex] approaches a number used so frequently in mathematics that it has its own name: the letter [latex]e[/latex]. This value is an irrational number, which means that its decimal expansion goes on forever without repeating. Its approximation to six decimal places is shown below.
A General Note: The Number [latex]e[/latex]
The letter e represents the irrational number
[latex]{\left(1+\frac{1}{n}\right)}^{n},\text{as }n\text{ increases without bound}[/latex]
The letter e is used as a base for many real-world exponential models. To work with base e, we use the approximation, [latex]e\approx 2.718282[/latex]. The constant was named by the Swiss mathematician Leonhard Euler (1707–1783) who first investigated and discovered many of its properties.
Example: Using a Calculator to Find Powers of [latex]e[/latex]
Calculate [latex]{e}^{3.14}[/latex]. Round to five decimal places.
Try It
Use a calculator to find [latex]{e}^{-0.5}[/latex]. Round to five decimal places.
Investigating Continuous Growth
So far we have worked with rational bases for exponential functions. For most real-world phenomena, however, e is used as the base for exponential functions. Exponential models that use e as the base are called continuous growth or decay models. We see these models in finance, computer science, and most of the sciences such as physics, toxicology, and fluid dynamics.
A General Note: The Continuous Growth/Decay Formula
For all real numbers t, and all positive numbers a and r, continuous growth or decay is represented by the formula
[latex]A\left(t\right)=a{e}^{rt}[/latex]
where
- a is the initial value
- r is the continuous growth rate per unit of time
- t is the elapsed time
If r > 0, then the formula represents continuous growth. If r < 0, then the formula represents continuous decay.
For business applications, the continuous growth formula is called the continuous compounding formula and takes the form
[latex]A\left(t\right)=P{e}^{rt}[/latex]
where
- P is the principal or the initial investment
- r is the growth or interest rate per unit of time
- t is the period or term of the investment
How To: Given the initial value, rate of growth or decay, and time t, solve a continuous growth or decay function
- Use the information in the problem to determine a, the initial value of the function.
- Use the information in the problem to determine the growth rate r.
- If the problem refers to continuous growth, then r > 0.
- If the problem refers to continuous decay, then r < 0.
- Use the information in the problem to determine the time t.
- Substitute the given information into the continuous growth formula and solve for A(t).
Example: Calculating Continuous Growth
A person invested $1,000 in an account earning a nominal interest rate of 10% per year compounded continuously. How much was in the account at the end of one year?
Try It
A person invests $100,000 at a nominal 12% interest per year compounded continuously. What will be the value of the investment in 30 years?
Example: Calculating Continuous Decay
Radon-222 decays at a continuous rate of 17.3% per day. How much will 100 mg of Radon-222 decay to in 3 days?
Try It
Using the data in the previous example, how much radon-222 will remain after one year?
- Todar, PhD, Kenneth. Todar's Online Textbook of Bacteriology. http://textbookofbacteriology.net/growth_3.html. ↵