Another Method For Converting From Base 10 to Other Bases

As you read the solution to this last example and attempted the “Try It” problems, you may have had to repeatedly stop and think about what was going on. The fact that you are probably struggling to follow the explanation and reproduce the process yourself is mostly due to the fact that the non-decimal systems are so unfamiliar to you. In fact, the only system that you are probably comfortable with is the decimal system.

As budding mathematicians, you should always be asking questions like “How could I simplify this process?” In general, that is one of the main things that mathematicians do: they look for ways to take complicated situations and make them easier or more familiar. In this section we will attempt to do that.

To do so, we will start by looking at our own decimal system. What we do may seem obvious and maybe even intuitive but that’s the point. We want to find a process that we readily recognize works and makes sense to us in a familiar system and then use it to extend our results to a different, unfamiliar system.

Let’s start with the decimal number, 4863₁₀. We will convert this number to base 10. Yeah, I know it’s already in base 10, but if you carefully follow what we’re doing, you’ll see it makes things work out very nicely with other bases later on. We first note that the highest power of 10 that will divide into 4863 at least once is 10³ = 1000. In general, this is the first step in our new process; we find the highest power of a given base that will divide at least once into our given number.

We now divide 1000 into 4863:

4863 ÷ 1000 = 4.863

This says that there are four thousands in 4863 (obviously). However, it also says that there are 0.863 thousands in 4863. This fractional part is our remainder and will be converted to lower powers of our base (10). If we take that decimal and multiply by 10 (since that’s the base we’re in) we get the following:

0.863 × 10 = 8.63

Why multiply by 10 at this point? We need to recognize here that 0.863 thousands is the same as 8.63 hundreds. Think about that until it sinks in.

(0.863)(1000) = 863
(8.63)(100) = 863

These two statements are equivalent. So, what we are really doing here by multiplying by 10 is rephrasing or converting from one place (thousands) to the next place down (hundreds).

0.863 × 10 ⇒ 8.63
(Parts of Thousands) × 10 ⇒ Hundreds

What we have now is 8 hundreds and a remainder of 0.63 hundreds, which is the same as 6.3 tens. We can do this again with the 0.63 that remains after this first step.

0.63 × 10 ⇒ 6.3
Hundreds × 10 ⇒ Tens

So we have six tens and 0.3 tens, which is the same as 3 ones, our last place value.

Now here’s the punch line. Let’s put all of the together in one place:

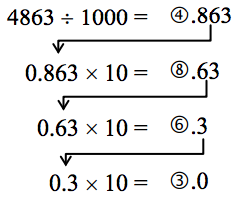
Note that in each step, the remainder is carried down to the next step and multiplied by 10, the base. Also, at each step, the whole number part, which is circled, gives the digit that belongs in that particular place. What is amazing is that this works for any base! So, to convert from a base 10 number to some other base, b, we have the following steps we can follow:

We will illustrate this procedure with some examples.

We can compare our result with what we saw earlier, or simply check with our calculator, and find that these two numbers really are equivalent to each other.

This last example shows the importance of using a calculator in certain situations and taking care to avoid clearing the calculator’s memory or display until you get to the very end of the process.

If we round, even to two decimal places in each step, clearing our calculator out at each step along the way, we will get a series of numbers that do not terminate, but begin repeating themselves endlessly. (Try it!) We end up with something that doesn’t make any sense, at least not in this context. So be careful to use your calculator cautiously on these conversion problems.

Also, remember that if your first division is by 7⁵, then you expect to have 6 digits in the final answer, corresponding to the places for 7⁵, 7⁴, and so on down to 7⁰. If you find yourself with more than 6 digits due to rounding errors, you know something went wrong.

The following video shows how to use a calculator to convert numbers in base 10 into other bases.