Learning Outcomes
- Become familiar with the history of positional number systems
- Identify bases that have been used in number systems historically
Background
As you might imagine, the development of a base system is an important step in making the counting process more efficient. Our own base-ten system probably arose from the fact that we have 10 fingers (including thumbs) on two hands. This is a natural development. However, other civilizations have had a variety of bases other than ten. For example, the Natives of Queensland used a base-two system, counting as follows: “one, two, two and one, two two’s, much.” Some Modern South American Tribes have a base-five system counting in this way: “one, two, three, four, hand, hand and one, hand and two,” and so on. The Babylonians used a base-sixty (sexigesimal) system. In this chapter, we wrap up with a specific example of a civilization that actually used a base system other than 10.
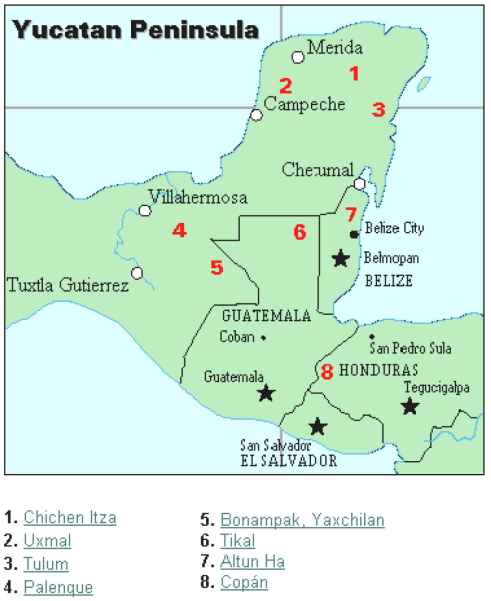 The Mayan civilization is generally dated from 1500 BCE to 1700 CE. The Yucatan Peninsula (see figure 16[1]) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. The Mayans had a sophisticated ritual system that was overseen by a priestly class. This class of priests developed a philosophy with time as divine and eternal.[2] The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. In fact, much of what we know about this culture comes from their calendar records and astronomy data. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549.
The Mayan civilization is generally dated from 1500 BCE to 1700 CE. The Yucatan Peninsula (see figure 16[1]) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. The Mayans had a sophisticated ritual system that was overseen by a priestly class. This class of priests developed a philosophy with time as divine and eternal.[2] The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. In fact, much of what we know about this culture comes from their calendar records and astronomy data. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549.
 There were two numeral systems developed by the Mayans—one for the common people and one for the priests. Not only did these two systems use different symbols, they also used different base systems. For the priests, the number system was governed by ritual. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads,[3] like the sample to the left[4] Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 360. This makes for a confusing system, the details of which we will skip.
There were two numeral systems developed by the Mayans—one for the common people and one for the priests. Not only did these two systems use different symbols, they also used different base systems. For the priests, the number system was governed by ritual. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads,[3] like the sample to the left[4] Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 360. This makes for a confusing system, the details of which we will skip.
Powers of numbers
Recall that powers of numbers indicate how many times to multiply the base. In the Mayan base 20 number system, the smallest place value is [latex]20^{0} = 1[/latex]. The next is [latex]20^{1}=20[/latex]. The third is [latex]20^{2}=400[/latex], and so on. See the table below for the base-ten values and Mayan names for each of the base 20 number positions.
| Powers | Base-Ten Value | Place Name |
| 207 | 12,800,000,000 | Hablat |
| 206 | 64,000,000 | Alau |
| 205 | 3,200,000 | Kinchil |
| 204 | 160,000 | Cabal |
| 203 | 8,000 | Pic |
| 202 | 400 | Bak |
| 201 | 20 | Kal |
| 200 | 1 | Hun |
The Mayan Number System
Instead, we will focus on the numeration system of the “common” people, which used a more consistent base system. As we stated earlier, the Mayans used a base-20 system, called the “vigesimal” system. Like our system, it is positional, meaning that the position of a numeric symbol indicates its place value. In the following table you can see the place value in its vertical format.[5]
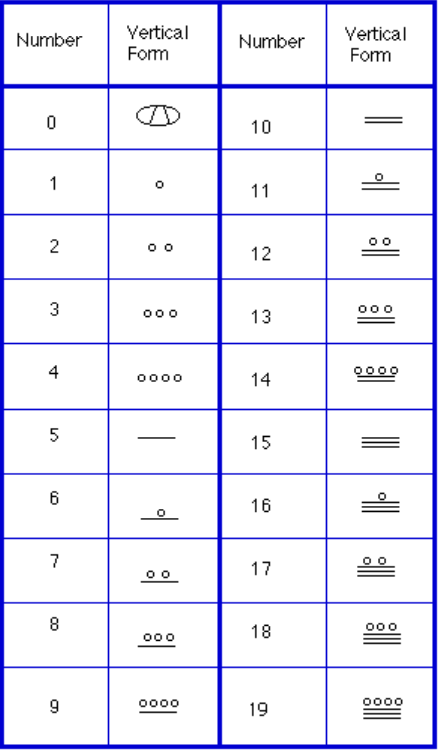
In order to write numbers down, there were only three symbols needed in this system. A horizontal bar represented the quantity 5, a dot represented the quantity 1, and a special symbol (thought to be a shell) represented zero. The Mayan system may have been the first to make use of zero as a placeholder/number. The first 20 numbers are shown in the table to the right.[6]
Unlike our system, where the ones place starts on the right and then moves to the left, the Mayan systems places the ones on the bottom of a vertical orientation and moves up as the place value increases.
When numbers are written in vertical form, there should never be more than four dots in a single place. When writing Mayan numbers, every group of five dots becomes one bar. Also, there should never be more than three bars in a single place…four bars would be converted to one dot in the next place up. It’s the same as 10 getting converted to a 1 in the next place up when we carry during addition.
Example
What is the value of this number, which is shown in vertical form?
![]()
Example
What is the value of the following Mayan number?
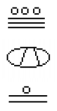
Try It
Convert the Mayan number below to base 10.

Example
Convert the base 10 number 357510 to Mayan numerals.
Writing numbers with bases bigger than 10
When the base of a number is larger than 10, separate each “digit” with a comma to make the separation of digits clear.
For example, in base 20, to write the number corresponding to 17 × 202 + 6 × 201 + 13 × 200, we’d write 17,6,1320.
Try It
Convert the base 10 number 1055310 to Mayan numerals.
Convert the base 10 number 561710 to Mayan numerals.
In the following video we present more examples of how to write numbers using Mayan numerals as well as converting numerals written in Mayan for into base 10 form.
The next video shows more examples of converting base 10 numbers into Mayan numerals.
Adding Mayan Numbers
When adding Mayan numbers together, we’ll adopt a scheme that the Mayans probably did not use but which will make life a little easier for us.
Try It
Try adding 174 and 78 in Mayan by first converting to Mayan numbers and then working entirely within that system. Do not add in base-ten (decimal) until the very end when you check your work.
In the last video we show more examples of adding Mayan numerals.
In this module, we have briefly sketched the development of numbers and our counting system, with the emphasis on the “brief” part. There are numerous sources of information and research that fill many volumes of books on this topic. Unfortunately, we cannot begin to come close to covering all of the information that is out there.
We have only scratched the surface of the wealth of research and information that exists on the development of numbers and counting throughout human history. What is important to note is that the system that we use every day is a product of thousands of years of progress and development. It represents contributions by many civilizations and cultures. It does not come down to us from the sky, a gift from the gods. It is not the creation of a textbook publisher. It is indeed as human as we are, as is the rest of mathematics. Behind every symbol, formula and rule there is a human face to be found, or at least sought.
Furthermore, we hope that you now have a basic appreciation for just how interesting and diverse number systems can get. Also, we’re pretty sure that you have also begun to recognize that we take our own number system for granted so much that when we try to adapt to other systems or bases, we find ourselves truly having to concentrate and think about what is going on.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Question ID 6420, 6423. Authored by: Morales,Lawrence. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Math in Society. Authored by: Lippman, David. Provided by: http://www.opentextbookstore.com/mathinsociety/. Located at: http://www.opentextbookstore.com/mathinsociety/. License: CC BY: Attribution
- The Mayan Number System: Writing Mayan Number in Base 10. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/gPUOrcilVS0. License: CC BY: Attribution
- The Mayan Number System: Writing Mayan Number in Base 10. Located at: https://youtu.be/LrHNXoqQ_lI. License: CC BY: Attribution
- The Mayan Number System: Addition of Mayan Numbers. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/NpH5oMCrubM. License: CC BY: Attribution
- http://www.gorp.com/gorp/location/latamer/map_maya.htm ↵
- Bidwell, James; Mayan Arithmetic in Mathematics Teacher, Issue 74 (Nov., 1967), p. 762–68. ↵
- http://www.ukans.edu/~lctls/Mayan/numbers.html ↵
- http://www.ukans.edu/~lctls/Mayan/numbers.html ↵
- Bidwell ↵
- http://www.vpds.wsu.edu/fair_95/gym/UM001.html ↵
- http://forum.swarthmore.edu/k12/mayan.math/mayan2.html ↵










