Learning Outcomes
- Use a geometry formula to set up a proportion in an application
Geometric shapes, as well as area and volumes, can often be important in problem solving.
Recall Solving a Proportion
A proportion is a given equivalency between two rates or ratios (fractions) in the form
[latex]\dfrac{a}{b}=\dfrac{c}{d}[/latex] where none of the given constants [latex]a, b, c, \text{ or } d[/latex] is equal to zero.
The unknown in a proportion may be located in any of the four positions, [latex]a, b, c, \text{ or } d[/latex]. The idea is to use multiplication and division as needed to isolate the unknown on one side of the equality symbol. Once that is accomplished we say that the equation is solved.
Ex 1. The unknown is in the numerator
[latex] \begin{align*} \dfrac{x}{b} &= \dfrac{c}{d} \quad \text{ multiply on both sides by } b \\ b\cdot \dfrac{x}{b} & =\dfrac{c}{d} \cdot b \\ x &= \dfrac{cb}{d} \end{align*} [/latex]
Ex 2. The unkown is in the denominator
[latex]\begin{align*} \dfrac{a}{x} &= \dfrac{c}{d} \\ x\cdot \dfrac{a}{x} &= \dfrac{c}{d} \cdot x \quad \text{ multiply on both sides by the reciprocal of } \dfrac{c}{d} \\ \dfrac{d}{c} \cdot \dfrac{a}{1} &= x\cdot \dfrac{c}{d} \cdot \dfrac{d}{c} \\ \dfrac{ad}{c} &= x \end{align*} [/latex]
Example
You are curious how tall a tree is, but don’t have any way to climb it. Describe a method for determining the height.
Similar Triangles
We introduced the idea of similar triangles in the previous example. One property of geometric shapes that we have learned is a helpful problem-solving tool is that of similarity. If two triangles are the same, meaning the angles between the sides are all the same, we can find an unknown length or height as in the last example. This idea of similarity holds for other geometric shapes as well.
Guided Example
Mary was out in the yard one day and had her two daughters with her. She was doing some renovations and wanted to know how tall the house was. She noticed a shadow 3 feet long when her daughter was standing 12 feet from the house and used it to set up figure 1.
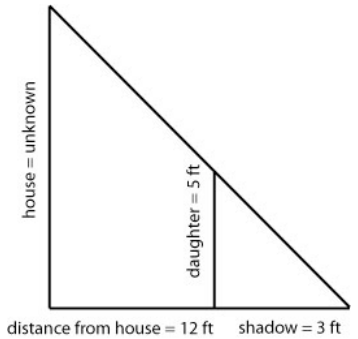
Figure 1.
We can take that drawing and separate the two triangles as follows allowing us to focus on the numbers and the shapes.
These triangles are what are called similar triangles. They have the same angles and sides in proportion to each other. We can use that information to determine the height of the house as seen in figure 2.
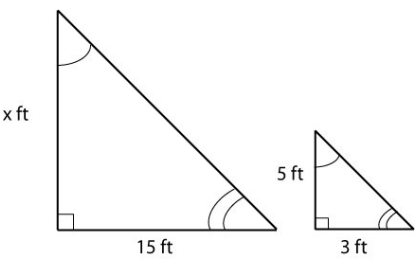
Figure 2.
To determine the height of the house, we set up the following proportion:
[latex]\displaystyle\frac{x}{15}=\frac{5}{3}\\[/latex]
Then, we solve for the unknown x by using multiplication to isolate it as we have done before:
[latex]\displaystyle{x}=\frac{5\times{15}}{3}=\frac{75}{3}=25\\[/latex]
Therefore, we can conclude that the house is 25 feet high.
Try It
It may be helpful to recall some formulas for areas and volumes of a few basic shapes:
Areas
| Rectangle | Circle, radius r |
| Area: [latex]L\times{W}[/latex] | Area: [latex]\pi{r^2}[/latex] |
| Perimeter: [latex]2l+2W[/latex] | Circumference[latex]2\pi{r}[/latex] |
Volumes
| Rectangular Box | Cylinder |
| Volume: [latex]L\times{W}\times{H}[/latex] | Volume: [latex]\pi{r^2}h[/latex] |
In our next two examples, we will combine the ideas we have explored about ratios with the geometry of some basic shapes to answer questions. In the first example, we will predict how much dough will be needed for a pizza that is 16 inches in diameter given that we know how much dough it takes for a pizza with a diameter of 12 inches. The second example uses the volume of a cylinder to determine the number of calories in a marshmallow.
Examples
If a 12 inch diameter pizza requires 10 ounces of dough, how much dough is needed for a 16 inch pizza?
The following video illustrates how to solve this problem.
Example
A company makes regular and jumbo marshmallows. The regular marshmallow has 25 calories. How many calories will the jumbo marshmallow have?
For more about the marshmallow example, watch this video.
Try It
1. A website says that you’ll need 48 fifty-pound bags of sand to fill a sandbox that measure 8ft by 8ft by 1ft. How many bags would you need for a sandbox 6ft by 4ft by 1ft?
2. Mary (from the application that started this topic), decides to use what she knows about the height of the roof to measure the height of her second daughter. If her second daughter casts a shadow that is 1.5 feet long when she is 13.5 feet from the house, what is the height of the second daughter? Draw an accurate diagram and use similar triangles to solve.
3.
In the next section, we will explore the process of combining different types of information to answer questions.
