Learning Outcomes
- Multiply fractions
- Multiply two or more fractions
- Multiply a fraction by a whole number
Introduction
Before we get started, here is some important terminology that will help you understand the concepts about working with fractions in this section.
- product: the result of multiplication
- factor: something being multiplied – for [latex]3 \cdot 2 = 6[/latex] , both 3 and 2 are factors of 6
- numerator: the top part of a fraction – the numerator in the fraction [latex]\frac{2}{3}[/latex] is 2
- denominator: the bottom part of a fraction – the denominator in the fraction [latex]\frac{2}{3}[/latex] is 3
Note About Instructions
Many different words are used by math textbooks and teachers to provide students with instructions on what they are to do with a given problem. For example, you may see instructions such as “Find” or “Simplify” in the example in this module. It is important to understand what these words mean so you can successfully work through the problems in this course. Here is a short list of the words you may see that can help you know how to work through the problems in this module.
| Instruction | Interpretation |
|---|---|
| Find | Perform the indicated mathematical operations which may include addition, subtraction, multiplication, division. |
| Simplify | 1) Perform the indicated mathematical operations including addition, subtraction, multiplication, division
2) Write a mathematical statement in smallest terms so there are no other mathematical operations that can be performed—often found in problems related to fractions and the order of operations |
| Evaluate | Perform the indicated mathematical operations including addition, subtraction, multiplication, division |
| Reduce | Write a mathematical statement in smallest or lowest terms so there are no other mathematical operations that can be performed—often found in problems related to fractions or division |
Multiply Fractions
Just as you add, subtract, multiply, and divide when working with whole numbers, you also use these operations when working with fractions. There are many times when it is necessary to multiply fractions. A model may help you understand multiplication of fractions.
When you multiply a fraction by a fraction, you are finding a “fraction of a fraction.” Suppose you have [latex]\frac{3}{4}[/latex] of a candy bar and you want to find [latex]\frac{1}{2}[/latex] of the [latex]\frac{3}{4}[/latex]:
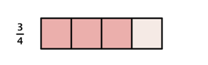
By dividing each fourth in half, you can divide the candy bar into eighths.

Then, choose half of those to get [latex]\frac{3}{8}[/latex].

In both of the above cases, to find the answer, you can multiply the numerators together and the denominators together.
Multiplying Two Fractions
[latex] \frac{a}{b}\cdot \frac{c}{d}=\frac{a\cdot c}{b\cdot d}=\frac{\text{product of the numerators}}{\text{product of the denominators}}[/latex]
Multiplying More Than Two Fractions
[latex] \frac{a}{b}\cdot \frac{c}{d}\cdot \frac{e}{f}=\frac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex]
Example
Multiply [latex] \frac{2}{3}\cdot \frac{4}{5}[/latex].
To review: if a fraction has common factors in the numerator and denominator, we can reduce the fraction to its simplified form by removing the common factors.
For example,
- Given [latex] \frac{8}{15}[/latex], the factors of 8 are: 1, 2, 4, 8 and the factors of 15 are: 1, 3, 5, 15. [latex] \frac{8}{15}[/latex] is simplified because there are no common factors of 8 and 15.
- Given [latex] \frac{10}{15}[/latex], the factors of 10 are: 1, 2, 5, 10 and the factors of15 are: 1, 3, 5, 15. [latex] \frac{10}{15}[/latex] is not simplified because 5 is a common factor of 10 and 15.
You can simplify first, before you multiply two fractions, to make your work easier. This allows you to work with smaller numbers when you multiply.
In the following video you will see an example of how to multiply two fractions, then simplify the answer.
Think About It
Multiply [latex] \frac{2}{3}\cdot \frac{1}{4}\cdot\frac{3}{5}[/latex]. Simplify the answer.
What makes this example different than the previous ones on this page? Use the box below to write down a few thoughts about how you would multiply three fractions together.
