Percent of a Whole

Percents are the ratio of a number and 100. Percents are used in many different applications. Percents are used widely to describe how something changed. For example, you may have heard that the amount of rainfall this month had decreased by 12% from last year, or that the number of jobless claims has increase by 5% this quarter over last quarter.

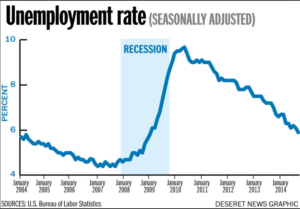
Unemployment rate as percent by year between 2004 and 2014.

We regularly use this kind of language to quickly describe how much something increased or decreased over time or between significant events.

Before we dissect the methods for finding percent change of a quantity, let’s learn the basics of finding percent of a whole.

For example, if we knew a gas tank held 14 gallons, and wanted to know how many gallons were in [latex]\frac{1}{4}[/latex] of a tank, we would find [latex]\frac{1}{4}[/latex] of 14 gallons by multiplying:

[latex] \frac{1}{4}\,\cdot \,14=\frac{1}{4}\,\cdot \,\frac{14}{1}=\frac{14}{4}=3\frac{2}{4}=3\frac{1}{2}\,\,\,\text{gallons}[/latex]

Likewise, if we wanted to find 25% of 14 gallons, we could find this by multiplying, but first we would need to convert the 25% to a decimal:

[latex]25\%\,\,\text{of}\,\,14\,\,\,\text{gallons}=0.25\,\cdot \,14=3.5\,\,\,\text{gallons}[/latex]

The following video contains an example that is similar to the one above.

From the previous example, we can identify three important parts to finding the percent of a whole:

• the percent,  has the percent symbol (%) or the word “percent”
• the amount, the amount is part of the whole
• and the base, the base is the whole amount

The following examples show how to identify the three parts: the percent, the base, and the amount.

The previous problem states that 30 is a portion of another number. That means 30 is the amount. Note that this problem could be rewritten: 20% of what number is 30?

The following video provides more examples that describe how to identify the percent, amount, and base in a percent problem.

In the next section, you will use the parts of a percent problem to find the percent increase or decrease of a quantity by writing and solving equations.

Percent Equations

Percent problems can be solved by writing equations. An equation uses an equal sign (=) to show that two mathematical expressions have the same value.

Percents are fractions, and just like fractions, when finding a percent (or fraction, or portion) of another amount, you multiply.

In the previous section, we identified three important parts to finding the percent of a whole:

• the percent, has the percent symbol (%) or the word “percent”
• the amount, the amount is part of the whole
• and the base, the base is the whole amount

Using these parts, we can define equations that will help us answer percent problems.

In the examples below, the unknown is represented by the letter n. The unknown can be represented by any letter or a box □, question mark, or even a smiley face :)

The following example shows how to use the percent equation to find the base in a percent equation.

Once you have an equation, you can solve it and find the unknown value. For example, to solve
[latex]20%\cdot{n}=30[/latex]

you can divide 30 by 20% to find the unknown:

[latex]20\%\cdot{n}=30[/latex]

You can solve this by writing the percent as a decimal or fraction and then dividing.

[latex]20\%\cdot{n}=30[/latex]

[latex]n=30\div20\%=30\div0.20=150[/latex]

In the following video example, you are shown how to use the percent equation to find the base in a percent problem.

You can estimate to see if the answer is reasonable. Use 10% and 20%, numbers close to 12.5%, to see if they get you close to the answer.

10% of 72 = 0.1 · 72 = 7.2

20% of 72 = 0.2 · 72 = 14.4

Notice that 9 is between 7.2 and 14.4, so 12.5% is reasonable since it is between 10% and 20%.

The video that follows shows how top use the percent equation to find the amount in a percent equation.