1. Explain the difference between a value at $x=a$ and the limit as $x$ approaches $a$.

2. Explain why we say a function does not have a limit as $x$ approaches $a$ if, as $x$ approaches $a$, the left-hand limit is not equal to the right-hand limit.

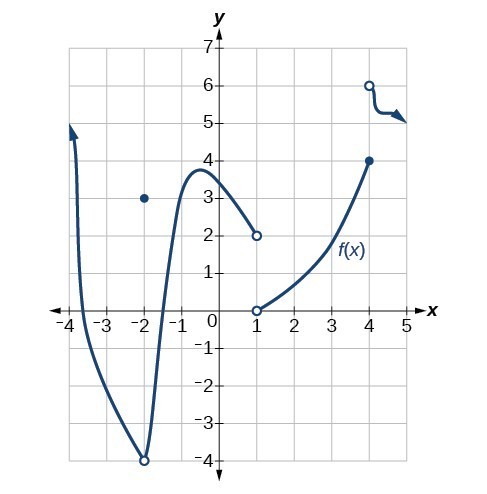
For the following exercises, estimate the functional values and the limits from the graph of the function $f$ provided in Figure 14.

3. $\underset{x\to -{2}^{-}}{\mathrm{lim}}f\left(x\right)$

4. $\underset{x\to -{2}^{+}}{\mathrm{lim}}f\left(x\right)$

5. $\underset{x\to -2}{\mathrm{lim}}f\left(x\right)$

6. $f\left(-2\right)$

7. $\underset{x\to -{1}^{-}}{\mathrm{lim}}f\left(x\right)$

8. $\underset{x\to {1}^{+}}{\mathrm{lim}}f\left(x\right)$

9. $\underset{x\to 1}{\mathrm{lim}}f\left(x\right)$

10. $f\left(1\right)$

11. $\underset{x\to {4}^{-}}{\mathrm{lim}}f\left(x\right)$

12. $\underset{x\to {4}^{+}}{\mathrm{lim}}f\left(x\right)$

13. $\underset{x\to 4}{\mathrm{lim}}f\left(x\right)$

14. $f\left(4\right)$

For the following exercises, draw the graph of a function from the functional values and limits provided.

15. $\underset{x\to {0}^{-}}{\mathrm{lim}}f\left(x\right)=2,\underset{x\to {0}^{+}}{\mathrm{lim}}f\left(x\right)=-3,\underset{x\to 2}{\mathrm{lim}}f\left(x\right)=2,f\left(0\right)=4,f\left(2\right)=-1,f\left(-3\right)\text{ does not exist}$.

16. $\underset{x\to {2}^{-}}{\mathrm{lim}}f\left(x\right)=0,\underset{x\to {2}^{+}}{\mathrm{lim}}=-2,\underset{x\to 0}{\mathrm{lim}}f\left(x\right)=3,f\left(2\right)=5,f\left(0\right)$

17. $\underset{x\to {2}^{-}}{\mathrm{lim}}f\left(x\right)=2,\underset{x\to {2}^{+}}{\mathrm{lim}}f\left(x\right)=-3,\underset{x\to 0}{\mathrm{lim}}f\left(x\right)=5,f\left(0\right)=1,f\left(1\right)=0$

18. $\underset{x\to {3}^{-}}{\mathrm{lim}}f\left(x\right)=0,\underset{x\to {3}^{+}}{\mathrm{lim}}f\left(x\right)=5,\underset{x\to 5}{\mathrm{lim}}f\left(x\right)=0,f\left(5\right)=4,f\left(3\right)\text{ does not exist}$.

19. $\underset{x\to 4}{\mathrm{lim}}f\left(x\right)=6,\underset{x\to {6}^{+}}{\mathrm{lim}}f\left(x\right)=-1,\underset{x\to 0}{\mathrm{lim}}f\left(x\right)=5,f\left(4\right)=6,f\left(2\right)=6$

20. $\underset{x\to -3}{\mathrm{lim}}f\left(x\right)=2,\underset{x\to {1}^{+}}{\mathrm{lim}}f\left(x\right)=-2,\underset{x\to 3}{\mathrm{lim}}f\left(x\right)=-4,f\left(-3\right)=0,f\left(0\right)=0$

21. $\underset{x\to \pi }{\mathrm{lim}}f\left(x\right)={\pi }^{2},\underset{x\to -\pi }{\mathrm{lim}}f\left(x\right)=\frac{\pi }{2},\underset{x\to {1}^{-}}{\mathrm{lim}}f\left(x\right)=0,f\left(\pi \right)=\sqrt{2},f\left(0\right)\text{ does not exist}$.

For the following exercises, use a graphing calculator to determine the limit to 5 decimal places as $x$ approaches 0.

22. $f\left(x\right)={\left(1+x\right)}^{\frac{1}{x}}$

23. $g\left(x\right)={\left(1+x\right)}^{\frac{2}{x}}$

24. $h\left(x\right)={\left(1+x\right)}^{\frac{3}{x}}$

25. $i\left(x\right)={\left(1+x\right)}^{\frac{4}{x}}$

26. $j\left(x\right)={\left(1+x\right)}^{\frac{5}{x}}$

27. Based on the pattern you observed in the exercises above, make a conjecture as to the limit of $f\left(x\right)={\left(1+x\right)}^{\frac{6}{x}}$, $g\left(x\right)={\left(1+x\right)}^{\frac{7}{x}}$, $\text{and }h\left(x\right)={\left(1+x\right)}^{\frac{n}{x}}$.

For the following exercises, use a graphing utility to find graphical evidence to determine the left- and right-hand limits of the function given as $x$ approaches $a$. If the function has a limit as $x$ approaches $a$, state it. If not, discuss why there is no limit.

28. $f\left(x\right)=\begin{cases}|x|-1,\hfill& \text{if }x\ne 1 \\ x^{3}, \hfill& \text{if }x=1\end{cases};\text{ }a=1$

29. $f\left(x\right)=\begin{cases}\dfrac{1}{x+1},\hfill& \text{if }x=−2 \\ \left(x+1\right)^{2},\hfill& \text{if }x\ne−2\end{cases};\text{ }a=−2$

For the following exercises, use numerical evidence to determine whether the limit exists at $x=a$. If not, describe the behavior of the graph of the function near $x=a$. Round answers to two decimal places.

30. $f\left(x\right)=\frac{{x}^{2}-4x}{16-{x}^{2}};a=4$

31. $f\left(x\right)=\frac{{x}^{2}-x - 6}{{x}^{2}-9};a=3$

32. $f\left(x\right)=\frac{{x}^{2}-6x - 7}{{x}^{2}- 7x};a=7$

33. $f\left(x\right)=\frac{{x}^{2}-1}{{x}^{2}-3x+2};a=1$

34. $f\left(x\right)=\frac{1-{x}^{2}}{{x}^{2}-3x+2};a=1$

35. $f\left(x\right)=\frac{10 - 10{x}^{2}}{{x}^{2}-3x+2};a=1$

36. $f\left(x\right)=\frac{x}{6{x}^{2}-5x - 6};a=\frac{3}{2}$

37. $f\left(x\right)=\frac{x}{4{x}^{2}+4x+1};a=-\frac{1}{2}$

38. $f\left(x\right)=\frac{2}{x - 4};\text{ }a=4$

For the following exercises, use a calculator to estimate the limit by preparing a table of values. If there is no limit, describe the behavior of the function as $x$ approaches the given value.

39. $\underset{x\to 0}{\mathrm{lim}}\dfrac{7\tan x}{3x}$

40. $\underset{x\to 4}{\mathrm{lim}}\dfrac{{x}^{2}}{x - 4}$

41. $\underset{x\to 0}{\mathrm{lim}}\dfrac{2\sin x}{4\tan x}$

For the following exercises, use a graphing utility to find numerical or graphical evidence to determine the left and right-hand limits of the function given as $x$ approaches $a$. If the function has a limit as $x$ approaches $a$, state it. If not, discuss why there is no limit.

42. $\underset{x\to 0}{\mathrm{lim}}{e}^{{e}^{\frac{1}{x}}}$

43. $\underset{x\to 0}{\mathrm{lim}}{e}^{{e}^{-\frac{1}{{x}^{2}}}}$

44. $\underset{x\to 0}{\mathrm{lim}}\dfrac{|x|}{x}$

45. $\underset{x\to -1}{\mathrm{lim}}\dfrac{|x+1|}{x+1}$

46. $\underset{x\to 5}{\mathrm{lim}}\dfrac{|x - 5|}{5-x}$

47. $\underset{x\to -1}{\mathrm{lim}}\dfrac{1}{{\left(x+1\right)}^{2}}$

48. $\underset{x\to 1}{\mathrm{lim}}\dfrac{1}{{\left(x - 1\right)}^{3}}$

49. $\underset{x\to 0}{\mathrm{lim}}\dfrac{5}{1-{e}^{\frac{2}{x}}}$

50. Use numerical and graphical evidence to compare and contrast the limits of two functions whose formulas appear similar: $f\left(x\right)=\left\rvert\frac{1-x}{x}\right\rvert$ and $g\left(x\right)=\left\rvert\frac{1+x}{x}\right\rvert$ as $x$ approaches 0. Use a graphing utility, if possible, to determine the left- and right-hand limits of the functions $f\left(x\right)$ and $g\left(x\right)$ as $x$ approaches 0. If the functions have a limit as $x$ approaches 0, state it. If not, discuss why there is no limit.

51. According to the Theory of Relativity, the mass $m$ of a particle depends on its velocity $v$ . That is

$m=\frac{{m}_{o}}{\sqrt{1-\left({v}^{2}/{c}^{2}\right)}}$

where ${m}_{o}$ is the mass when the particle is at rest and $c$ is the speed of light. Find the limit of the mass, $m$, as $v$ approaches ${c}^{-}$.

52. Allow the speed of light, $c$, to be equal to 1.0. If the mass, $m$, is 1, what occurs to $m$ as $v\to c?$ Using the values listed in the table below, make a conjecture as to what the mass is as $v$ approaches 1.00.

$v$	$m$
0.5	1.15
0.9	2.29
0.95	3.20
0.99	7.09
0.999	22.36
0.99999	223.61