1. Give an example of a type of function [latex]f[/latex] whose limit, as [latex]x[/latex] approaches [latex]a[/latex], is [latex]f\left(a\right)[/latex].

2. When direct substitution is used to evaluate the limit of a rational function as [latex]x[/latex] approaches [latex]a[/latex] and the result is [latex]f\left(a\right)=\frac{0}{0}[/latex], does this mean that the limit of [latex]f[/latex] does not exist?

3. What does it mean to say the limit of [latex]f\left(x\right)[/latex], as [latex]x[/latex] approaches [latex]c[/latex], is undefined?

For the following exercises, evaluate the limits algebraically.

4. [latex]\underset{x\to 0}{\mathrm{lim}}\left(3\right)[/latex]

5. [latex]\underset{x\to 2}{\mathrm{lim}}\left(\dfrac{-5x}{{x}^{2}-1}\right)[/latex]

6. [latex]\underset{x\to 2}{\mathrm{lim}}\left(\dfrac{{x}^{2}-5x+6}{x+2}\right)[/latex]

7. [latex]\underset{x\to 3}{\mathrm{lim}}\left(\dfrac{{x}^{2}-9}{x - 3}\right)[/latex]

8. [latex]\underset{x\to -1}{\mathrm{lim}}\left(\dfrac{{x}^{2}-2x - 3}{x+1}\right)[/latex]

9. [latex]\underset{x\to \frac{3}{2}}{\mathrm{lim}}\left(\dfrac{6{x}^{2}-17x+12}{2x - 3}\right)[/latex]

10. [latex]\underset{x\to -\frac{7}{2}}{\mathrm{lim}}\left(\dfrac{8{x}^{2}+18x - 35}{2x+7}\right)[/latex]

11. [latex]\underset{x\to 3}{\mathrm{lim}}\left(\dfrac{{x}^{2}-9}{x - 5x+6}\right)[/latex]

12. [latex]\underset{x\to -3}{\mathrm{lim}}\left(\dfrac{-7{x}^{4}-21{x}^{3}}{-12{x}^{4}+108{x}^{2}}\right)[/latex]

13. [latex]\underset{x\to 3}{\mathrm{lim}}\left(\dfrac{{x}^{2}+2x - 3}{x - 3}\right)[/latex]

14. [latex]\underset{h\to 0}{\mathrm{lim}}\left(\dfrac{{\left(3+h\right)}^{3}-27}{h}\right)[/latex]

15. [latex]\underset{h\to 0}{\mathrm{lim}}\left(\dfrac{{\left(2-h\right)}^{3}-8}{h}\right)[/latex]

16. [latex]\underset{h\to 0}{\mathrm{lim}}\left(\dfrac{{\left(h+3\right)}^{2}-9}{h}\right)[/latex]

17. [latex]\underset{h\to 0}{\mathrm{lim}}\left(\dfrac{\sqrt{5-h}-\sqrt{5}}{h}\right)[/latex]

18. [latex]\underset{x\to 0}{\mathrm{lim}}\left(\dfrac{\sqrt{3-x}-\sqrt{3}}{x}\right)[/latex]

19. [latex]\underset{x\to 9}{\mathrm{lim}}\left(\dfrac{{x}^{2}-81}{3-\sqrt{x}}\right)[/latex]

20. [latex]\underset{x\to 1}{\mathrm{lim}}\left(\dfrac{\sqrt{x}-{x}^{2}}{1-\sqrt{x}}\right)[/latex]

21. [latex]\underset{x\to 0}{\mathrm{lim}}\left(\dfrac{x}{\sqrt{1+2x}-1}\right)[/latex]

22. [latex]\underset{x\to \frac{1}{2}}{\mathrm{lim}}\left(\dfrac{{x}^{2}-\frac{1}{4}}{2x - 1}\right)[/latex]

23. [latex]\underset{x\to 4}{\mathrm{lim}}\left(\dfrac{{x}^{3}-64}{{x}^{2}-16}\right)[/latex]

24. [latex]\underset{x\to {2}^{-}}{\mathrm{lim}}\left(\dfrac{|x - 2|}{x - 2}\right)[/latex]

25. [latex]\underset{x\to {2}^{+}}{\mathrm{lim}}\left(\dfrac{|x - 2|}{x - 2}\right)[/latex]

26. [latex]\underset{x\to 2}{\mathrm{lim}}\left(\dfrac{|x - 2|}{x - 2}\right)[/latex]

27. [latex]\underset{x\to {4}^{-}}{\mathrm{lim}}\left(\dfrac{|x - 4|}{4-x}\right)[/latex]

28. [latex]\underset{x\to {4}^{+}}{\mathrm{lim}}\left(\dfrac{|x - 4|}{4-x}\right)[/latex]

29. [latex]\underset{x\to 4}{\mathrm{lim}}\left(\dfrac{|x - 4|}{4-x}\right)[/latex]

30. [latex]\underset{x\to 2}{\mathrm{lim}}\left(\dfrac{-8+6x-{x}^{2}}{x - 2}\right)[/latex]

For the following exercise, use the given information to evaluate the limits: [latex]\underset{x\to c}{\mathrm{lim}}f\left(x\right)=3[/latex], [latex]\underset{x\to c}{\mathrm{lim}}g\left(x\right)=5[/latex]

31. [latex]\underset{x\to c}{\mathrm{lim}}\left[2f\left(x\right)+\sqrt{g\left(x\right)}\right][/latex]

32. [latex]\underset{x\to c}{\mathrm{lim}}\left[3f\left(x\right)+\sqrt{g\left(x\right)}\right][/latex]

33. [latex]\underset{x\to c}{\mathrm{lim}}\frac{f\left(x\right)}{g\left(x\right)}[/latex]

For the following exercises, evaluate the following limits.

34. [latex]\underset{x\to 2}{\mathrm{lim}}\cos \left(\pi x\right)[/latex]

35. [latex]\underset{x\to 2}{\mathrm{lim}}\sin \left(\pi x\right)[/latex]

36. [latex]\underset{x\to 2}{\mathrm{lim}}\sin \left(\frac{\pi }{x}\right)[/latex]

37. [latex]{f}\left(x\right)=\begin{cases}2x^{2}+2x+1, \hfill& x\leq0 \\ x-3, \hfill& x>0\end{cases};\underset{x\to 0^{+}}{\mathrm{lim}}f \left(x\right)[/latex]

38. [latex]{f}\left(x\right)=\begin{cases}2x^{2}+2x+1, \hfill& x\leq0 \\ x-3, \hfill& x>0\end{cases};\underset{x\to 0^{-}}{\mathrm{lim}}f \left(x\right)[/latex]

39. [latex]{f}\left(x\right)=\begin{cases}2x^{2}+2x+1, \hfill& x\leq0 \\ x-3, \hfill& x>0\end{cases};\underset{x\to 0}{\mathrm{lim}}f \left(x\right)[/latex]

40. [latex]\underset{x\to 4}{\mathrm{lim}}\dfrac{\sqrt{x+5}-3}{x - 4}[/latex]

41. [latex]\underset{x\to {3}^{+}}{\mathrm{lim}}\dfrac{{x}^{2}}{{x}^{2}-9}[/latex]

For the following exercises, find the average rate of change [latex]\frac{f\left(x+h\right)-f\left(x\right)}{h}[/latex].

42. [latex]f\left(x\right)=x+1[/latex]

43. [latex]f\left(x\right)=2{x}^{2}-1[/latex]

44. [latex]f\left(x\right)={x}^{2}+3x+4[/latex]

45. [latex]f\left(x\right)={x}^{2}+4x - 100[/latex]

46. [latex]f\left(x\right)=3{x}^{2}+1[/latex]

47. [latex]f\left(x\right)=\cos \left(x\right)[/latex]

48. [latex]f\left(x\right)=2{x}^{3}-4x[/latex]

49. [latex]f\left(x\right)=\frac{1}{x}[/latex]

50. [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex]

51. [latex]f\left(x\right)=\sqrt{x}[/latex]

52. Find an equation that could be represented by Figure 2.

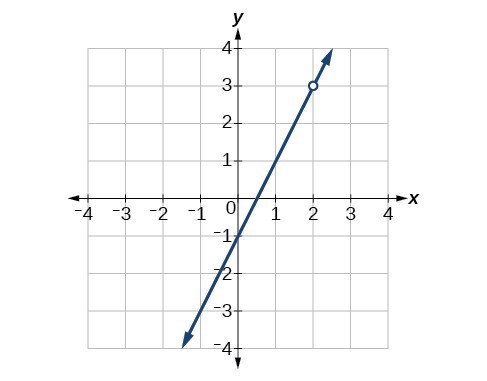
Figure 2

53. Find an equation that could be represented by Figure 3.

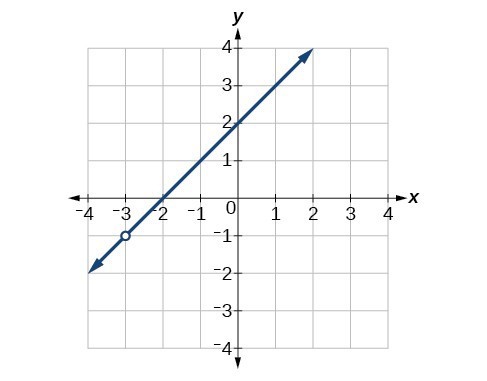
Figure 4

For the following exercises, refer to Figure 4.

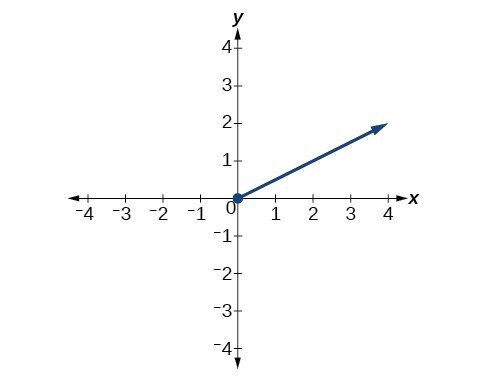
Figure 5

54. What is the right-hand limit of the function as [latex]x[/latex] approaches 0?

55. What is the left-hand limit of the function as [latex]x[/latex] approaches 0?

56. The position function [latex]s\left(t\right)=-16{t}^{2}+144t[/latex] gives the position of a projectile as a function of time. Find the average velocity (average rate of change) on the interval [latex]\left[1,2\right][/latex] .

57. The height of a projectile is given by [latex]s\left(t\right)=-64{t}^{2}+192t[/latex] Find the average rate of change of the height from [latex]t=1[/latex] second to [latex]t=1.5[/latex] seconds.

58. The amount of money in an account after [latex]t[/latex] years compounded continuously at 4.25% interest is given by the formula [latex]A={A}_{0}{e}^{0.0425t}[/latex], where [latex]{A}_{0}[/latex] is the initial amount invested. Find the average rate of change of the balance of the account from [latex]t=1[/latex] year to [latex]t=2[/latex] years if the initial amount invested is $1,000.00.