section 3.2 Learning Objectives
3.2: Introduction to Functions
- Determine if a relation is a function
- Identify the domain and range of a set of ordered pairs
- Evaluate a function written in function notation
- Find the domain of a rational function
There are many kinds of relations. A relation is simply a correspondence between sets of values or information. Think about members of your family and their ages. The pairing of each member of your family and their age is a relation. Each family member can be paired with an age in the set of ages of your family members. Another example of a relation is the pairing of a state with its U.S. senators. Each state can be matched with two individuals who have each been elected to serve as a senator. In turn, each senator can be matched with one specific state that he or she represents. Both of these are real-life examples of relations.
Determine if a relation is a function
The first value of a relation is an input value and the second value is the output value. A function is a specific type of relation in which each input value has one and only one output value. An input is the independent value, and the output is the dependent value, as it depends on the value of the input.
Which set of values make up the input values and output values can affect whether or not the relation is a function. Notice in the first table below, where the input is “name” and the output is “age,” each input matches with exactly one output. This is an example of a function.
| Family Member’s Name (Input) | Family Member’s Age (Output) |
|---|---|
| Nellie | [latex]13[/latex] |
| Marcos | [latex]11[/latex] |
| Esther | [latex]46[/latex] |
| Samuel | [latex]47[/latex] |
| Nina | [latex]47[/latex] |
| Paul | [latex]47[/latex] |
| Katrina | [latex]21[/latex] |
| Andrew | [latex]16[/latex] |
| Maria | [latex]13[/latex] |
| Ana | [latex]81[/latex] |
Compare this with the next table where the input is “age” and the output is “name.” Some of the inputs result in more than one output. This is an example of a correspondence that is not a function.
| Family Member’s Age (Input) | Family Member’s Name (Output) |
|---|---|
| [latex]11[/latex] | Marcos |
| [latex]13[/latex] | Nellie, Maria |
| [latex]16[/latex] | Andrew |
| [latex]21[/latex] | Katrina |
| [latex]46[/latex] | Esther |
| [latex]47[/latex] | Samuel, Nina, Paul |
| [latex]81[/latex] | Ana |
Now let us look at some other examples to determine whether the relations are functions or not and under what circumstances. Remember that a relation is a function if there is only one output for each input.
Example 1
Fill in the table.
| Input | Output | Function? | Why or why not? |
|---|---|---|---|
| Name of senator | Name of state | ||
| Name of state | Name of senator | ||
| Time elapsed | Height of a tossed ball | ||
| Height of a tossed ball | Time elapsed | ||
| Number of cars | Number of tires | ||
| Number of tires | Number of cars |
Relations can be written as ordered pairs of numbers or as numbers in a table of values. Unless stated otherwise, the first number of an ordered pair is the x-value and is the input, while the second number is the y-value and is the output. By examining the inputs (x-coordinates) and outputs (y-coordinates), you can determine whether or not the relation is a function. Remember, in a function, each input has only one output.
Identify the domain and range of a set of ordered pairs
There is a name for the set of input values and another name for the set of output values for a function. The set of input values is called the domain of the function. The set of output values is called the range of the function.
If you have a set of ordered pairs, you can find the domain by listing all of the input values, which are the x-coordinates. To find the range, list all of the output values, which are the y-coordinates.
Consider the following set of ordered pairs:
[latex]\{(−2,0),(0,6),(2,12),(4,18)\}[/latex]
You have the following:
[latex]\begin{array}{l}\text{Domain:}\{−2,0,2,4\}\\\text{Range:}\{0,6,12,18\}\end{array}[/latex]
Now try it yourself.
Example 2
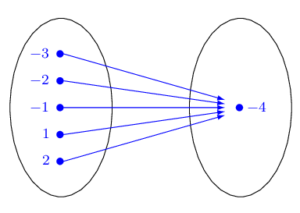
List the domain and range for the following table of values where x is the input and y is the output. Then determine if the relation is a function.
| x | y |
|---|---|
| [latex]−3[/latex] | [latex]4[/latex] |
| [latex]−2[/latex] | [latex]4[/latex] |
| [latex]−1[/latex] | [latex]4[/latex] |
| [latex]2[/latex] | [latex]4[/latex] |
| [latex]3[/latex] | [latex]4[/latex] |
In the following video we provide another example of identifying whether a table of values represents a function as well as determining the domain and range of each.
Example 3
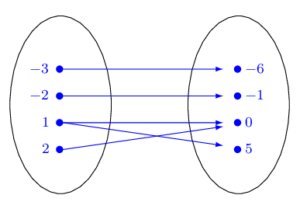
Define the domain and range for the following set of ordered pairs, and determine whether the relation given is a function.
[latex]\{(−3,−6),(−2,−1),(1,0),(1,5),(2,0)\}[/latex]
In the following video, we show how to determine whether a relation is a function and how to find the domain and range.
Summary: Determining Whether a Relation is a Function
- Identify the input values – this is your domain.
- Identify the output values – this is your range.
- If each value in the domain leads to only one value in the range, classify the relationship as a function. If any value in the domain leads to two or more values in the range, do not classify the relationship as a function.
Function notation
Some people think of functions as “mathematical machines.” Imagine you have a machine that changes a number according to a specific rule such as “multiply by [latex]3[/latex] and add [latex]2[/latex]” or “divide by [latex]5[/latex], add [latex]25[/latex], and multiply by [latex]−1[/latex].” If you put a number into the machine, a new number will pop out the other end having been changed according to the rule. The number that goes in is called the input, and the number that is produced is called the output.
You can also call the machine “f” for function. If you put x into the machine, f(x), comes out. Mathematically speaking, x is the input, or the “independent variable,” and f(x) is the output, or the “dependent variable,” since it depends on the value of x.
[latex]f(x)=4x+1[/latex] is written in function notation and is read “f of x equals [latex]4x[/latex] plus 1” It represents the following situation: A function named f acts upon an input, x, and produces f(x) which is equal to [latex]4x+1[/latex]. This is the same as the equation [latex]y=4x+1[/latex].
Function notation gives you more flexibility because you do not have to use [latex]y[/latex] for every equation. Instead, you could use [latex]f(x)[/latex] or [latex]g(x)[/latex] or even [latex]c(x)[/latex]. This can be a helpful way to distinguish equations of functions when you are dealing with more than one at a time.
Using Function Notation
Once we determine that a relationship is a function, we need to display and define the functional relationship so that we can understand it, use it, and possibly even program it into a computer. There are various ways of representing functions. A standard function notation is one representation that facilitates working with functions.
A General Note: Function Notation
The notation [latex]y=f\left(x\right)[/latex] defines a function named [latex]f[/latex]. This is read as “[latex]y[/latex] is a function of [latex]x[/latex].” The letter [latex]x[/latex] represents the input value, or independent variable. The letter [latex]y[/latex] or [latex]f\left(x\right)[/latex], represents the output value, or dependent variable.
Example 4
Use function notation to represent a function whose input is the name of a month and output is the number of days in that month.
Note that the inputs to a function do not have to be numbers; function inputs can be names of people, labels of geometric objects, or any other element that determines some kind of output. However, most of the functions we will work with here will have numbers as inputs and outputs.
Example 5
A function [latex]f\left(y\right)=N[/latex] gives the number of police officers, [latex]N[/latex], in a town in year [latex]y[/latex]. What does [latex]f\left(2005\right)=300[/latex] represent?
In the following videos we show two more examples of how to express a relationship using function notation.
Evaluating a function written in function notation
Throughout this course, you have been and will continue working with algebraic equations. Many of these equations are functions. For example, [latex]y=4x+1[/latex] is an equation that represents a function. When you input values for x, you can determine a single output for y. In this case, if you substitute [latex]x=10[/latex] into the equation you will find that y must be [latex]41[/latex]; there is no other value of y that would make the equation true.
Rather than using the variable y, the equations of functions can be written using function notation. Function notation is very useful when you are working with more than one function at a time and substituting more than one value in for x.
Equations written using function notation can also be evaluated. With function notation, you might see the following:
Given [latex]f(x)=4x+1[/latex], find [latex]f(2)[/latex].
You read this problem like this: “given [latex]f[/latex] of [latex]x[/latex] equals [latex]4x[/latex] plus one, find [latex]f[/latex] of [latex]2[/latex].” While the notation and wording is different, the process of evaluating a function is the same as evaluating an expression at a specific value. In both cases, you substitute [latex]2[/latex] for [latex]x[/latex], multiply it by [latex]4[/latex] and add [latex]1[/latex], simplifying to get [latex]9[/latex]. In this function, an input of [latex]2[/latex] results in an output of [latex]9[/latex].
[latex]f(x)=4x+1\\f(2)=4(2)+1=8+1=9[/latex]
You can simply apply what you already know about evaluating expressions to evaluate a function. It is important to note that the parentheses that are part of function notation do not mean multiply. The notation [latex]f(x)[/latex] does not mean [latex]f[/latex] multiplied by [latex]x[/latex]. Instead, the notation means “[latex]f[/latex]of [latex]x[/latex]” or “the function of [latex]x[/latex].” To evaluate the function, take the value given for [latex]x[/latex], and substitute that value in for [latex]x[/latex] in the expression. Let us look at a couple of examples.
Example 6
Given [latex]f(x)=3x–4[/latex], find [latex]f(5)[/latex].
Functions can be evaluated for negative values of x, too. Keep in mind the rules for integer operations.
Example 7
Given [latex]p(x)=2x^{2}+5[/latex], find [latex]p(−3)[/latex].
You may also be asked to evaluate a function for more than one value as shown in the example that follows.
Example 8
Given [latex]f(x)=|4x-3|[/latex], find [latex]f(0)[/latex], [latex]f(2)[/latex], and [latex]f(−1)[/latex].
Next we look at an example where one of the inputs leads to a problem.
Example 9
Given [latex]f(x)=\displaystyle{ \frac{2x}{x+4}}[/latex], find [latex]f(0)[/latex], [latex]f(3)[/latex], and [latex]f(-4)[/latex].
Finding the domain of a rational function
The previous example has an important implication about the domain of this fractional function, called a rational function. Expanding upon our earlier definition of domain, the domain of a function is the set of input values that lead to valid output values. It follows that for the function [latex]f(x)=\frac{2x}{x+4}[/latex], [latex]x=-4[/latex] is not in the domain. Moreover, we can see that [latex]-4[/latex] is the only value of [latex]x[/latex] that results in a zero denominator, so the domain is all [latex]x[/latex]-values except [latex]x=-4[/latex]. In set-builder notation, we would write the domain as [latex]\{x|x\neq -4\}[/latex].
We conclude this section with an example that explicitly asks for the domain of a rational function.
Example 10
Find the domain of [latex]f(x)=\displaystyle{\frac{1}{3x+4}}[/latex].
Candela Citations
- Modified from Beginning and Intermediate Algebra. Authored by: Tyler Wallace. License: CC BY: Attribution
- Provided by: Openstax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface.%20. License: CC BY: Attribution
- Ex: Function Notation Application Problem. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/lF0fzdaxU_8. License: CC BY: Attribution
- Function Notation Application. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/nAF_GZFwU1g. License: CC BY: Attribution
- Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface. License: CC BY: Attribution. License Terms: Download for free at : http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@3.278:1/Preface
- Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/y2TqnP_6M1s. License: CC BY: Attribution