section 3.5 Learning Objectives
3.5: Applications of Slope
- Find the average rate of change
- Use a linear equation to make a prediction
In the previous section, we learned how to find the slope of a line. In this section we will look at applications of slope and the corresponding linear functions.
Rate and Unit Rate
A rate is a ratio of two quantities with different units. The presence of units implies that this is a concept used in many real world applications. Often, it is useful to simplify a rate to a unit rate, which has a denominator of 1.
Example 1
A. Suppose you drive 216 miles on 9 gallons of gas. Express the rate and the unit rate comparing miles traveled to gallons of gas used.
B. If you instead drove 223 miles on 9 gallons of gas, compute the miles traveled per gallon of gas. Round your answer to the nearest tenth.
Find the average rate of change
A rate of change is a rate comparing the relative changes in two related variables. “Change” is computing by finding the difference between two. Does a fraction comparing the differences in two variables sound familiar? If you are thinking slope, you are correct!
The slope of a function that describes, real, measurable quantities is a rate of change. In these functions, the slope describes the change in one quantity per change in another quantity. We can use what we know about slope to find the rate of change.
Previously, we learned that Slope = [latex]\frac{\text{Rise}}{\text{Run}}[/latex]. We will use this definition to find the rate of change in the following example.
A candle has a starting length of 10 inches. Thirty minutes after lighting it, the length is 7 inches. Determine the rate of change in the length of the candle as it burns.
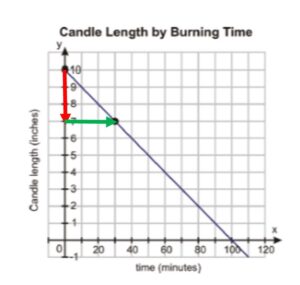
The graph shows the candle length as a function of time. The horizontal axis is time in minutes and the vertical axis is the candle length in inches. Since the candle has a starting length of 10 inches, we can represent that on the graph by the point (0, 10). After 30 minutes, the candle is 7 inches. This can be represented by the point (30, 7). To find the rate of change, we need to determine the slope of the line.
Rate of Change = Slope = [latex]\frac{\text{Rise}}{\text{Run}}[/latex]
Look at the points (0, 10) and (30, 7) on the graph. To move from (0, 10) to (30, 7) we would go down 3 units and to the right 30 units. Be sure to pay attention to the scale of each axis. Therefore, the Rise would be -3. (It is negative because we went down instead of up.) The Run would be 30.
Rate of Change = Slope = [latex]\frac{\text{Rise}}{\text{Run}}=\frac{-3\text{ inches}}{30 \text{ minutes}}=-0.1[/latex] inches per minute
So, the candle length is decreasing by 0.1 inches each minute.
We could also find the rate of change using the two ordered pairs and the following definition of slope:
Rate of Change = Slope= [latex]\frac{y_2-y_1}{x_2-x_1}=\frac{7\text{ inches}-10\text{ inches}}{30\text{ minutes}- 0\text{ minutes}}=\frac{-3\text{ inches}}{30\text{ minutes}}=-0.1[/latex] inches per minute.
In this candle example, the scales on the x-axis and y-axis were different from each other. The y-axis was in units of 1, while the x-axis was in units of 10. If you’d like to see another example of how to find the slope (or rate of change) of a line with different scales on the axes, see the video below:
Example 2
Given the information in the table below, what is the average rate of change in the number of living wage jobs from 1998 to 2000?
Living Wage Jobs
| Year | 1998 | 1999 | 2000 | 2001 |
| Jobs | 685 | 722 | 760 | 798 |
Example 3
A city’s population in 2012 was 3,267,100. In 2002, the population was 3,289,200. What is the average rate of change in the population per year from 2002 to 2012?
Example 4
On a bicycle, Michelle rides for 3 hours and is 35 miles from her house. After riding for 10 hours, she is 112 miles away. What is Michelle’s average rate in miles per hour during her trip?
Use a linear model to make a prediction
In the first two examples, we will be given the equation and asked to make a prediction about the data using that equation.
Example 5
The following linear model describes the change in median home values in Hawaii between 1950 and 2000.
[latex]f(x)=3966x+74,400[/latex]
where [latex]x=[/latex] the number of years since 1950, and [latex]f(x)=[/latex] the median value of a house.
Use this linear model to predict the median value of a house in Hawaii in the year 2022.
Sometimes when a linear model represents a set of data or observations, the y-intercept can be interpreted as a starting point. Let’s look at the previous example and determine what the y-intercept represents.
The y-intercept of any equation is the point where the x-coordinate is 0. Substituting into the linear model give us the following:
[latex]f(x)=3966x+74,400[/latex]
[latex]f(0)=3966(0)+74,400[/latex]
[latex]f(0)=74,400[/latex]
What does this result mean? Since [latex]x[/latex] represents the number of years since 1950, [latex]x=0[/latex] would represent the year 1950. Therefore, [latex]f(0)=74,400[/latex] means that in 1950 the median value of a house in Hawaii was $74,400.
The following video shows another example of how to make a prediction with the home value data.
Example 6
Data on tuition and mid-career salary were collected from a number of universities and colleges. The result of the data collection is the following linear model:
[latex]f(x)=-0.97x+159,000[/latex]
where [latex]x=[/latex] annual tuition, and [latex]f(x)=[/latex] average mid-career salary of graduates.
A. What is the slope of this linear model?
B. According to this model, what is the average salary for a graduate of a college or university where the annual tuition is $30,000?
C. According to this model, what happens to mid-career salary as tuition increases?
Example 7
The cost to produce Mario’s Skyrockets is given by the following linear model:
[latex]C(x)=25x+840[/latex]
where [latex]x=[/latex] the number of skyrockets produced, and [latex]C(x)=[/latex] the total cost.
Use this linear model to predict:
A. What is the slope?
B. What is the cost to produce 20 skyrockets?
C. According to this model, what happens to cost as the number of rockets produced increases?
The following video gives another example where we must solve for the x-value.
Summary
In this section we looked at a couple of applications of slope and linear models. We learned that in a real world context, slope represents the average rate of change. This leads to linear functions that can be used to model such real world situations. These models can then be used to make predictions for given inputs.