**As of Fall 2023, Math 0990 is no longer using this module. Students working on an “Incomplete” prior to Fall 2023 will still need this module**
section 8.1 Learning Objectives
8.1: Revisiting Domain
- Determine the domain of a function given an equation
- Find the domain of a polynomial
- Find the domain of a square root function
- Find the domain of a non-even root
- Find the domain of a rational function
Recall from section 3.2, functions are a correspondence between two sets, called the domain and the range. We previously practiced finding the domain and range of a set of ordered pairs, but now we will look at finding the domain when given the equation of a function.
When defining a function, we usually state what kind of numbers the domain and range values can be. But even if we say the values are real numbers, that does not mean that all real numbers can be used for [latex]x[/latex]. It also does not mean that all real numbers can be function values, [latex]f(x)[/latex]. There may be restrictions on the domain (and range). The restrictions partly depend on the type of function.
Restrictions on Domain
There are two main reasons domain will be restricted for a function (that we focus on in this course). Any input value that would ask the function to violate one (or both) of the rules below, creates a restriction on the domain because those values cannot be allowed to be input into the function. (Hint: If you try to input either of these things in your calculator, it will give you a “Domain Error” message as the output message).
Reasons for Restricting the Domain of a function
-
We cannot take the square (or other even) root of a negative number. The result will not be a real number.
-
We cannot divide by [latex]0[/latex].
These two issues would be of concern when the function is either of the following:
- A radical function with an even index (such as a square root), where the radicand (quantity under the radical) could potentially be negative for some value or values of x. [latex]f\left(x\right)=\sqrt{7-x}[/latex] is a radical function.
- A rational function where the denominator could potentially become [latex]0[/latex] for some value or values of x, [latex]f\left(x\right)=\dfrac{5}{2-x}[/latex] is an example of a rational function.
The following table gives examples of domain restrictions for several different radical functions. Roots of negative numbers will be an issue whenever the function has a variable under a radical with an even root. Look at the following examples and note that “square root of a negative variable” doesn’t necessarily mean that the value under the radical sign is negative. For example, if [latex]x=−4[/latex], then [latex]−x=−(−4)=4[/latex], a positive number.
| Function | Restrictions to the Domain |
|---|---|
| [latex] f(x)=\sqrt{x}[/latex] | If [latex]x<0[/latex], we would be taking the square root of a negative number, so instead of allowing [latex]x[/latex] to be any real number, we restrict the domain down to [latex]x\geq0[/latex]. |
| [latex] f(x)=\sqrt{x+10}[/latex] | If [latex]x<−10[/latex], we would be taking the square root of a negative number, so [latex]x\geq−10[/latex]. |
| [latex] f(x)=\sqrt{-x}[/latex] | When is [latex]-x[/latex] negative? Only when [latex]x[/latex] is positive. (For example, if [latex]x=1[/latex], then [latex]−x=-1[/latex]. But if [latex]x=-3[/latex], then [latex]−x=-(-3)=3[/latex].)This means [latex]x\leq0[/latex]. |
| [latex] f(x)=\sqrt{{{x}^{2}}-1}[/latex] | [latex]x^{2}–1[/latex] must be positive, [latex]x^{2}–1>0[/latex]. So [latex]x^{2}>1[/latex]. This happens only when x is greater than 1 or less than [latex]−1[/latex]: [latex]x\leq−1[/latex] or [latex]x\geq1[/latex]. |
| [latex] f(x)=\sqrt{{{x}^{2}}+10}[/latex] | There are no domain restrictions even though there is a variable under the radical. Since [latex]x^{2}\ge0[/latex], [latex]x^{2}+10[/latex] can never be negative. The least it can be is [latex]\sqrt{10}[/latex], so there is no danger of taking the square root of a negative number. |
The following table gives examples of domain restrictions for several different rational functions. Note that a rational function has the variable present in the denominator.
| Function | Restrictions to the Domain |
|---|---|
| [latex] f(x)=\dfrac{1}{x}[/latex] | If [latex]x=0[/latex], we would be dividing by [latex]0[/latex], so [latex]x\neq0[/latex]. |
| [latex] f(x)=\dfrac{2+x}{x-3}[/latex] | If [latex]x=3[/latex], we would be dividing by [latex]0[/latex], so [latex]x\neq3[/latex]. |
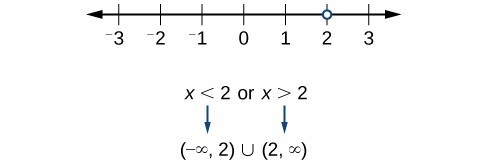
| [latex] f(x)=\dfrac{2(x-1)}{x-1}[/latex] | Although you can simplify this function to [latex]f(x)=2[/latex], when [latex]x=1[/latex], the original function would include division by [latex]0[/latex], so [latex]x\neq1[/latex]. |
| [latex] f(x)=\dfrac{x}{{{x}^{2}}-1}[/latex] | Both [latex]x=1[/latex] and [latex]x=−1[/latex] would make the denominator 0, so [latex]x\neq1[/latex] and [latex]x\neq−1[/latex]. |
| [latex] f(x)=\dfrac{2}{{{x}^{2}}+1}[/latex] | This is an example with no domain restrictions, even though there is a variable in the denominator. Since [latex]x^{2}\geq0,x^{2}+1[/latex] can never be [latex]0[/latex]. The least it can be is [latex]1[/latex], so there is no danger of division by [latex]0[/latex]. |
So, how exactly do you define the domain of a function?
How To find the domain, Given a function written in equation form
- Identify the input values.
- Identify any restrictions on the input and exclude those values from the domain.
- Is there an even index on a radical in the function? If so there may be restrictions on values related to this.
- Is there a fraction with a variable in the denominator in the function? If so there may be restrictions on values related to this.
- Write the domain in interval notation (or Set-Builder Notation), if possible.
Example 1
Find the domain of the function [latex]f\left(x\right)={x}^{2}-1[/latex].
How To find the domain, Given a function written in equation form including an even root
- Identify the input values.
- Since there is an even root, we want to exclude any real numbers that result in a negative number in the radicand from being in the domain. Set the radicand greater than or equal to zero and solve for [latex]x[/latex]. (Any numbers not in the solution are values restricted from the domain.)
- The solution(s) from step 2 are the domain of the function. If possible, write the answer in interval form.
Example 2
Find the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].
Example 3
Find the domain of the function [latex]f\left(x\right)=\sqrt[3]{-2x-3}[/latex].
Below is another example of finding the domain of a radical function:
How To find the domain, Given a function written in equation form that includes a fraction
- Identify the input values.
- Identify any restrictions on the input.
- If there is a denominator in the function’s formula with variables in it, set the denominator equal to zero and solve for [latex]x[/latex] . These values are restricted from the domain.
- If the function also contains an even root, set the radicand greater than or equal to [latex]0[/latex] and then solve. Any numbers not in the solution are restricted values from the domain.
- Write the domain in interval form, making sure to exclude any restricted values from the domain.
Example 4
Find the domain of the function [latex]f\left(x\right)=\dfrac{x+1}{2-x}[/latex].
Watch the video below for another description of domain as well as some more examples involving radical functions and rational functions: