1.7 Section Exercises
Verbal
1. When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal stretch from a vertical stretch?
2. When examining the formula of a function that is the result of multiple transformations, how can you tell a horizontal compression from a vertical compression?
Algebraic
3. Write a formula for the function obtained when the graph of [latex]f\left(x\right)=\sqrt[\leftroot{1}\uproot{2} ]{x}[/latex] is vertically stretched by a factor of 4.
4. Write a formula for the function obtained when the graph of [latex]f\left(x\right)=\sqrt[\leftroot{1}\uproot{2} ]{x}[/latex] is vertically compressed by a factor of 1/3.
5. Write a formula for the function obtained when the graph of [latex]f\left(x\right)=|x|[/latex] is horizontally stretched by a factor of 5.
6. Write a formula for the function obtained when the graph of [latex]f\left(x\right)=|x|[/latex] is horizontally compressed by a factor of 1/4.
7. Write a formula for the function obtained when the graph of [latex]f\left(x\right)=\sqrt[\leftroot{1}\uproot{2} ]{x}[/latex] is horizontally stretched by a factor of 3 and vertically stretched by a factor of 6.
8. Write a formula for the function obtained when the graph of [latex]f\left(x\right)=|x|[/latex] is horizontally compressed by a factor of 1/2 and vertically compressed by a factor of 1/7.
For the following exercises, write a formula for the function[latex]\text{ }g\text{ }[/latex]that results when the graph of a given toolkit function is transformed as described.
9. The graph of[latex]\text{ }f\left(x\right)=|x|\text{ }[/latex]is reflected over the[latex]\text{ }y[/latex]–axis and horizontally compressed by a factor of[latex]\text{ }\frac{1}{4}[/latex] .
10. The graph of[latex]\text{ }f\left(x\right)=\sqrt[\leftroot{1}\uproot{2} ]{x}\text{ }[/latex]is reflected over the[latex]\text{ }x[/latex]-axis and horizontally stretched by a factor of 2.
11. The graph of[latex]\text{ }f\left(x\right)=\frac{1}{{x}^{2}}\text{ }[/latex]is vertically compressed by a factor of[latex]\text{ }\frac{1}{3},\text{ }[/latex]then shifted to the left 2 units and down 3 units.
12. The graph of[latex]\text{ }f\left(x\right)=\frac{1}{x}\text{ }[/latex]is vertically stretched by a factor of 8, then shifted to the right 4 units and up 2 units.
13. The graph of[latex]\text{ }f\left(x\right)={x}^{2}\text{ }[/latex]is vertically compressed by a factor of[latex]\text{ }\frac{1}{2},\text{ }[/latex]then shifted to the right 5 units and up 1 unit.
14. The graph of[latex]\text{ }f\left(x\right)={x}^{2}\text{ }[/latex]is horizontally stretched by a factor of 3, then shifted to the left 4 units and down 3 units.
For the following exercises, describe how the graph of the function is a transformation of the graph of the original function[latex]\text{ }f.[/latex]
15. [latex]h\left(x\right)=3f\left(x\right)[/latex]
16. [latex]g\left(x\right)=0.5f\left(x\right)[/latex]
17. [latex]g\left(x\right)=-f\left(x\right)[/latex]
18. [latex]g\left(x\right)=f\left(-x\right)[/latex]
19. [latex]g\left(x\right)=4f\left(x\right)[/latex]
20. [latex]g\left(x\right)=6f\left(x\right)[/latex]
21. [latex]g\left(x\right)=f\left(5x\right)[/latex]
22. [latex]g\left(x\right)=f\left(2x\right)[/latex]
23. [latex]g\left(x\right)=f\left(\frac{1}{3}x\right)[/latex]
24. [latex]g\left(x\right)=f\left(\frac{1}{5}x\right)[/latex]
25. [latex]g\left(x\right)=3f\left(-x\right)[/latex]
For the following exercises, determine the interval(s) on which the function is increasing and decreasing.
26. [latex]f\left(x\right)=4{\left(x+1\right)}^{2}-5[/latex]
27. [latex]g\left(x\right)=5{\left(x+3\right)}^{2}-2[/latex]
28. [latex]a\left(x\right)=\sqrt[\leftroot{1}\uproot{2} ]{-x+4}[/latex]
29. [latex]k\left(x\right)=-3\sqrt[\leftroot{1}\uproot{2} ]{x}-1[/latex]
Graphical
For the following exercises, use the graph of[latex]\text{ }f\left(x\right)={2}^{x}\text{ }[/latex]shown in Figure 1 to sketch a graph of each transformation of[latex]\text{ }f\left(x\right).[/latex]
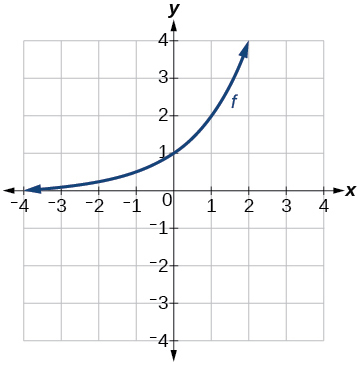
Figure 1
30. [latex]g\left(x\right)=3\left({2}^{x}\right)+1[/latex]
31. [latex]w\left(x\right)=-4{2}^{x-1}[/latex]
For the following exercises, sketch a graph of the function as a transformation of the graph of one of the toolkit functions.
32. [latex]f\left(t\right)=4{\left(t+1\right)}^{2}-3[/latex]
33. [latex]h\left(x\right)=-2|x-1|+4[/latex]
34. [latex]k\left(x\right)={\left(0.5x-2\right)}^{3}-1[/latex]
35. [latex]m\left(t\right)=3+\sqrt[\leftroot{1}\uproot{2} ]{0.25t+2}[/latex]
Numeric
36. Tabular representations for the functions[latex]\text{ }f,\text{ }g,\text{ }[/latex]and[latex]\text{ }h\text{ }[/latex]are given below. Write[latex]\text{ }g\left(x\right)\text{ }[/latex]and[latex]\text{ }h\left(x\right)\text{ }[/latex]as transformations of[latex]\text{ }f\left(x\right).[/latex]
| [latex]x[/latex] | −2 | −1 | 0 | 1 | 2 |
| [latex]f\left(x\right)[/latex] | −1 | −3 | 4 | 2 | 1 |
| [latex]x[/latex] | −4 | −2 | 0 | 2 | 4 |
| [latex]g\left(x\right)[/latex] | −1 | −3 | 4 | 2 | 1 |
| [latex]x[/latex] | −2 | −1 | 0 | 1 | 2 |
| [latex]h\left(x\right)[/latex] | 3 | 9 | -12 | -6 | -3 |
37. Tabular representations for the functions[latex]\text{ }f,\text{ }g,\text{ }[/latex]and[latex]\text{ }h\text{ }[/latex]are given below. Write[latex]\text{ }g\left(x\right)\text{ }[/latex]and[latex]\text{ }h\left(x\right)\text{ }[/latex]as transformations of[latex]\text{ }f\left(x\right).[/latex]
| [latex]x[/latex] | −2 | −1 | 0 | 1 | 2 |
| [latex]f\left(x\right)[/latex] | −2 | −1 | −3 | 1 | 2 |
| [latex]x[/latex] | −1 | -1/2 | 0 | 1/2 | 1 |
| [latex]g\left(x\right)[/latex] | −2 | −1 | −3 | 1 | 2 |
| [latex]x[/latex] | −2 | −1 | 0 | 1 | 2 |
| [latex]h\left(x\right)[/latex] | −4 | -2 | -6 | 2 | 4 |
For the following exercises, write an equation for each graphed function by using transformations of the graphs of one of the toolkit functions.
For the following exercises, describe how the formula is a transformation of a toolkit function. Then sketch a graph of the transformation.
41. [latex]g\left(x\right)=4{\left(x+1\right)}^{2}-5[/latex]
42. [latex]g\left(x\right)=5{\left(x+3\right)}^{2}-2[/latex]
43. [latex]h\left(x\right)=-2|x-4|+3[/latex]
44. [latex]k\left(x\right)=-3\sqrt[\leftroot{1}\uproot{2} ]{x}-1[/latex]
45. [latex]m\left(x\right)=\frac{1}{2}{x}^{3}[/latex]
46. [latex]n\left(x\right)=\frac{1}{3}|x-2|[/latex]
47. [latex]p\left(x\right)={\left(\frac{1}{3}x\right)}^{3}-3[/latex]
48. [latex]q\left(x\right)={\left(\frac{1}{4}x\right)}^{3}+1[/latex]
49. [latex]a\left(x\right)=\sqrt[\leftroot{1}\uproot{2} ]{-x+4}[/latex]
For the following exercises, use the graph in Figure 2 to sketch the given transformations.
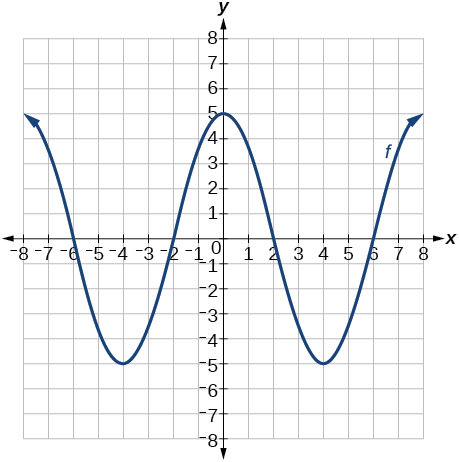
Figure 2.
50. [latex]g\left(x\right)=f\left(x\right)-2[/latex]
51. [latex]g\left(x\right)=-f\left(x\right)[/latex]
52. [latex]g\left(x\right)=f\left(2x\right)[/latex]
53. [latex]g\left(x\right)=f\left(x-2\right)[/latex]







