Simple description

Let’s first consider the pi bond in ethene from a simplified MO theory standpoint (in this example we will be disregarding the sigma bonds in the molecule, and thinking only about the π bond). We start with two atomic orbitals: one unhybridized 2p orbital from each carbon. Each contains a single electron. In MO theory, the two atomic combine mathematically to form two pi molecular orbitals, one a low-energy pi bonding orbital and one a high-energy pi* antibonding orbital.

Molecular orbitals for ethene (ethylene)

In the bonding pi orbital, the two shaded lobes of the p orbitals interact constructively with each other, as do the two unshaded lobes (remember, the arbitrary shading choice represents mathematical (+) and (-) signs for the mathematical wavefunction describing the orbital). There is increased electron density between the two carbon nuclei in the molecular orbital – it is a bonding interaction.

In the higher-energy antibonding pi* orbital, the shaded lobe of one p orbital interacts destructively with the unshaded lobe of the second p orbital, leading to a node between the two nuclei and overall repulsion between the carbon nuclei.

Again using the ‘building up’ principle, we place the two electrons in the lower-energy, bonding pi molecular orbital. The antibonding pi* orbital remains empty.

More detailed MO description of ethene

Molecular orbital theory has been very successfully applied to large conjugated systems, especially those containing chains of carbon atoms with alternating single and double bonds. An approximation introduced by Hü​ckel in 1931 considers only the delocalized p electrons moving in a framework of $$\pi$$-bonds. This is, in fact, a more sophisticated version of a free-electron model.  For an introductory organic chemistry course we do not need to use all of Hü​ckel’s mathematics, but for those who like to probe deeper, a more detailed analysis is given here.

The simplest hydrocarbon to consider that exhibits $$\pi$$ bonding is ethene (ethylene), which is made up of four hydrogen atoms and two carbon atoms. Experimentally, we know that the H–C–H and H–C–C angles in ethene are approximately 120°. This angle suggests that the carbon atoms are sp² hybridized, which means that a singly occupied sp² orbital on one carbon overlaps with a singly occupied s orbital on each H and a singly occupied sp² lobe on the other C. Thus each carbon forms a set of three$$\sigma$$ bonds: two C–H (sp² + s) and one C–C (sp² + sp²) (part (a) of Figure 13.1. below).

Figure 13.1. (a) The σ-bonded framework is formed by the overlap of two sets of singly occupied carbon sp² hybrid orbitals and four singly occupied hydrogen 1s orbitals to form electron-pair bonds. This uses 10 of the 12 valence electrons to form a total of five σ bonds (four C–H bonds and one C–C bond). (b) One singly occupied unhybridized 2pz orbital remains on each carbon atom to form a carbon–carbon π bond. (Note: by convention, in planar molecules the axis perpendicular to the molecular plane is the z-axis.)

The Hückel approximation is used to determine the energies and shapes of the $$\pi$$ molecular orbitals in conjugated systems. Within the Hückel approximation, the covalent bonding in these hydrocarbons can be separated into two independent “frameworks”: the $$\sigma$$-bonding framework and the the $$\sigma$$-bonding framework. The wavefunctions used to describe the bonding orbitals in each framework results from different combinations of atomic orbitals. The method limits itself to addressing conjugated hydrocarbons and specifically only $$\pi$$ electron molecular orbitals are included because these determine the general properties of these molecules; the sigma electrons are ignored. This is referred to as sigma-pi separability and is justified by the orthogonality of $$\sigma$$ and $$\pi$$ orbitals in planar molecules. For this reason, the Hückel method is limited to planar systems. Hückel approximation assumes that the electrons in the $$\pi$$ bonds “feel” an electrostatic potential due to the entire $$\sigma$$-bonding framework in the molecule (i.e. it focuses only on the formation of $$\pi$$ bonds, given that the $$\sigma$$ bonding framework has already been formed).

Ethene

Before considering the Hückel treatment for ethene, it is beneficial to review the general bonding picture of the molecule. Bonding in ethene involves the $$sp^2$$ hybridization of the $$2s$$, $$2p_x$$, and $$2p_y$$ atomic orbitals on each carbon atom; leaving the $$2p_z$$ orbitals untouched (Figure 13.2).

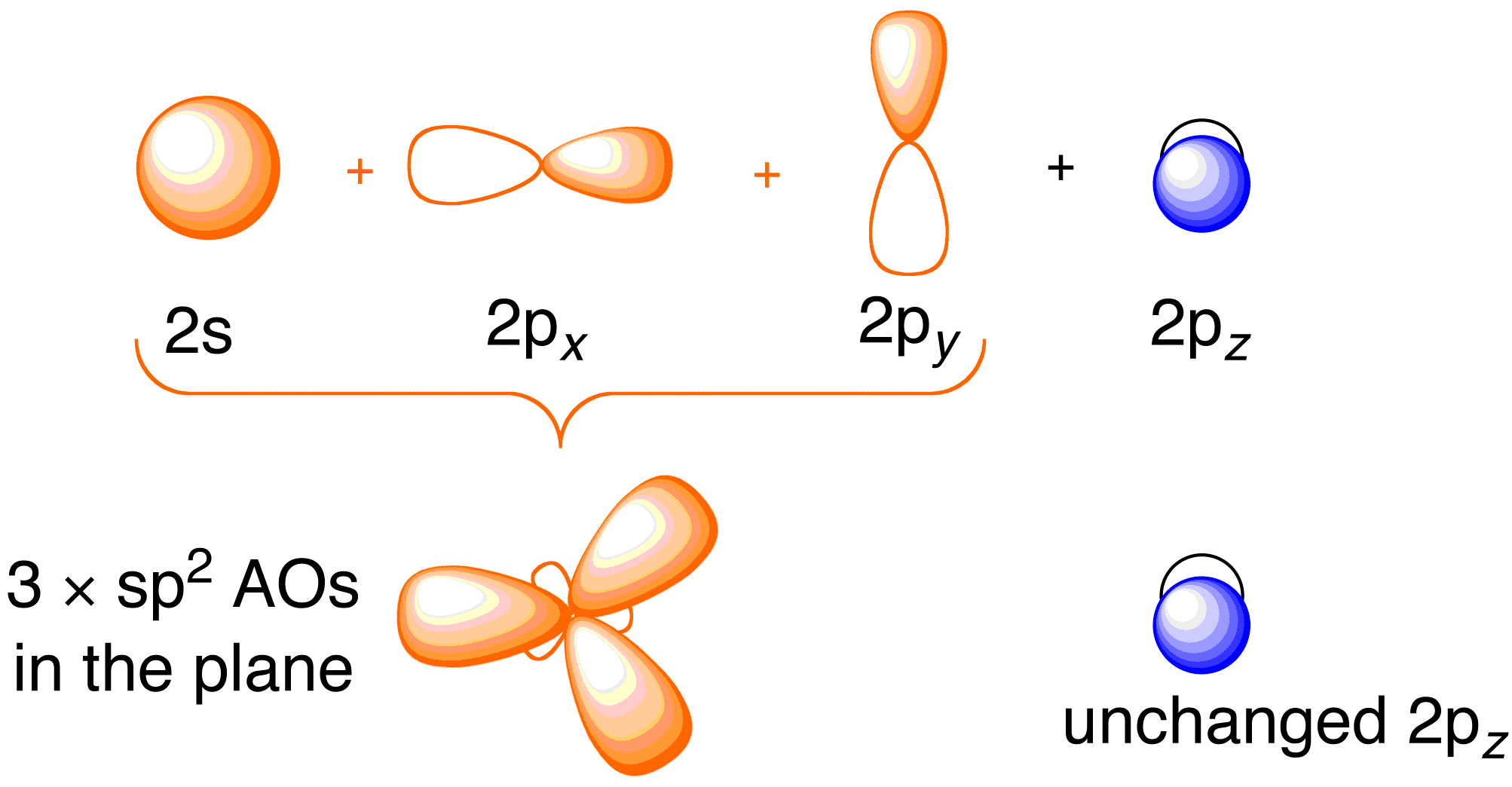
Figure 13.2. Hybridizing of the carbon atomic orbitals to give $$sp^2$$ hybrid orbitals for bonding to hydrogen atoms in ethene. Image used with permission from ChemTube (CC-SA-BY-NC; Nick Greeves).

The use of hybrid orbitals in the molecular orbital approach describe here is merely a convenience and not invoking valence bond theory (directly). An identical description can be extracted using exclusively atomic orbitals on carbon, but the interpretation of the resulting wavefunctions is less intuitive. For example, the i^th molecular orbital can be described via hybrid orbitals

\[ | \psi_1\rangle = c_1 | sp^2_1 \rangle + c_2 | 1s_a \rangle \nonumber\]

or via atomic orbitals.

\[ | \psi_1\rangle = a_1 | 2s \rangle + a_1 | 2p_x \rangle + a_1 | 2p_y \rangle + a_4| 1s_a \rangle \nonumber\]

where $$\{a_i\}$$ and $$\{c_i\}$$ are coefficients of the expansion. Either describe will work and both are identical approaches since

\[| sp^2_1 \rangle = b_1 | 2s \rangle + b_1 | 2p_x \rangle + b_1 | 2p_y \rangle \nonumber\]

where $$\{c_i\}$$ are coefficients describing the hybridized orbital.

The bonding occurs via the mixing of the electrons in the $$sp^2$$ hybrid orbitals on carbon and the electrons in the $$1s$$ atomic orbitals of the four hydrogen atoms (Figure 13.2. above left) resulting in the $$\sigma$$-bonding framework. The $$\pi$$-bonding framework results from the unhybridized $$2p_z$$ orbitals (Figure 13.2. above, right). The independence of these two frameworks is demonstrated in the resulting molecular orbital diagram in the Figure below; Hückel theory is concerned only with describing the molecular orbitals and energies of the $$\pi$$ bonding framework.

Figure 13.3: Molecular orbitals demonstrating the sigma-pi separability of the $$\pi$$-bonding framework (blue) and the $$\sigma$$-bonding frameworks (red) of ethylene.

Hückel treatment is concerned only with describing the molecular orbitals and energies of the $$\pi$$ bonding framework.

Since Hückel theory is a special consideration of molecular orbital theory, the molecular orbitals $$| \psi_i \rangle$$ can be described as a linear combination of the $$2p_z$$ atomic orbitals $$\phi$$ at carbon with their corresponding $$\{c_i\}$$ coefficients:

\[ | \psi_i \rangle =c_1 | \phi_{1} \rangle +c_2 | \phi_2 \rangle \label{LCAO} \]

For the complete quantum chemistry analysis using the Schrödinger equation (not required for the organic chemistry class), see this Libretexts page.

These molecular orbitals form the π-bonding framework and since each carbon contributes one electron to this framework, only the lowest molecular orbital ($$ | \psi_1 \rangle$$) is occupied (Figure ) in the ground state. The corresponding electron configuration is then $$ \pi_1^2$$.

Figure 13.4: Schemetic representation of the $$\pi$$ molecular orbitals framework for ethylene . Notice that the antibonding molecular orbital has one more node than the bonding molecular orbital as expected since it is higher in energy.

 

HOMO and LUMO are acronyms for highest occupied molecular orbital and lowest unoccupied molecular orbital, respectively and are often referred to as frontier orbitals. The energy difference between the HOMO and LUMO is termed the HOMO–LUMO gap.

The 3-D calculated $$\pi$$ molecular orbitals are shown in Figure 13.5.

Figure 13.5: Calculated $$\pi$$ molecular orbitals for ethylene . (left) the bonding orbital (ψ₁) and (right) the antibonding (ψ₂) orbital.