We finish our discussion of the hypothesis test for a population mean with a review of the meaning of the P-value, along with a review of type I and type II errors.

Review of the Meaning of the P-value

At this point, we assume you know how to use a P-value to make a decision in a hypothesis test. The logic is always the same. If we pick a level of significance (α), then we compare the P-value to α.

• If the P-value ≤ α, reject the null hypothesis. The data supports the alternative hypothesis.

• If the P-value > α, do not reject the null hypothesis. The data is not strong enough to support the alternative hypothesis.

In fact, we find that we treat these as “rules” and apply them without thinking about what the P-value means. So let’s pause here and review the meaning of the P-value, since it is the connection between probability and decision-making in inference.

What Does the P-Value of 0.082 Tell Us?

A simulation can help us understand the P-value. In a simulation, we assume that the population mean is 3,500 grams. This is the null hypothesis. We assume the null hypothesis is true and select 1,000 random samples from a population with a mean of 3,500 grams. The mean of the sampling distribution is at 3,500 (as predicted by the null hypothesis.) We see this in the simulated sampling distribution.

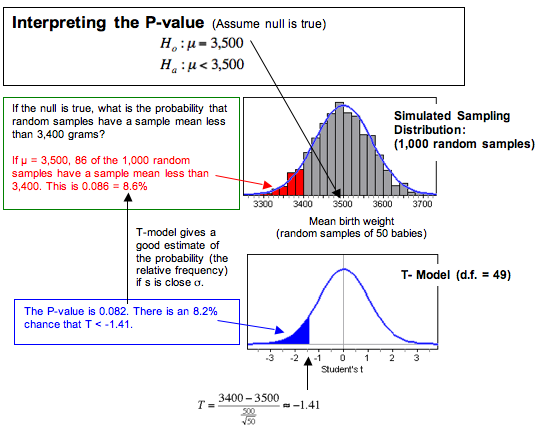
In the simulation, we can see that about 8.6% of the samples have a mean less than 3,400. Since probability is the relative frequency of an event in the long run, we say there is an 8.6% chance that a random sample of 500 babies has a mean less than 3,400 if the population mean is 3,500. We can see that the corresponding area to the left of T = −1.41 in the T-model (with df = 49) also gives us a good estimate of the probability. This area is the P-value, about 8.2%.

If we generalize this statement, we say the P-value is the probability that random samples have results more extreme than the data if the null hypothesis is true. (By more extreme, we mean further from value of the parameter, in the direction of the alternative hypothesis.) We can also describe the P-value in terms of T-scores. The P-value is the probability that the test statistic from a random sample has a value more extreme than that associated with the data if the null hypothesis is true.

Review of Type I and Type II Errors

We know that statistical inference is based on probability, so there is always some chance of making a wrong decision. Recall that there are two types of wrong decisions that can be made in hypothesis testing. When we reject a null hypothesis that is true, we commit a type I error. When we fail to reject a null hypothesis that is false, we commit a type II error.

The following table summarizes the logic behind type I and type II errors.

It is possible to have some influence over the likelihoods of committing these errors. But decreasing the chance of a type I error increases the chance of a type II error. We have to decide which error is more serious for a given situation. Sometimes a type I error is more serious. Other times a type II error is more serious. Sometimes neither is serious.

Recall that if the null hypothesis is true, the probability of committing a type I error is α. Why is this? Well, when we choose a level of significance (α), we are choosing a benchmark for rejecting the null hypothesis. If the null hypothesis is true, then the probability that we will reject a true null hypothesis is α. So the smaller α is, the smaller the probability of a type I error.

It is more complicated to calculate the probability of a type II error. The best way to reduce the probability of a type II error is to increase the sample size. But once the sample size is set, larger values of α will decrease the probability of a type II error (while increasing the probability of a type I error).

General Guidelines for Choosing a Level of Significance

• If the consequences of a type I error are more serious, choose a small level of significance (α).
• If the consequences of a type II error are more serious, choose a larger level of significance (α). But remember that the level of significance is the probability of committing a type I error.
• In general, we pick the largest level of significance that we can tolerate as the chance of a type I error.

Let’s Summarize

In this “Hypothesis Test for a Population Mean,” we looked at the four steps of a hypothesis test as they relate to a claim about a population mean.

Step 1: Determine the hypotheses.

• The hypotheses are claims about the population mean, µ.
• The null hypothesis is a hypothesis that the mean equals a specific value, µ₀.
• The alternative hypothesis is the competing claim that µ is less than, greater than, or not equal to the [latex]{\mathrm{μ}}_{0}[/latex] .
  • When [latex]{H}_{a}[/latex] is [latex]μ[/latex] < [latex]{μ}_{0}[/latex] or [latex]μ[/latex] > [latex]{μ}_{0}[/latex] , the test is a one-tailed test.
  • When [latex]{H}_{a}[/latex] is [latex]μ[/latex] ≠ [latex]{μ}_{0}[/latex] , the test is a two-tailed test.

Step 2: Collect the data.

Since the hypothesis test is based on probability, random selection or assignment is essential in data production. Additionally, we need to check whether the t-model is a good fit for the sampling distribution of sample means. To use the t-model, the variable must be normally distributed in the population or the sample size must be more than 30. In practice, it is often impossible to verify that the variable is normally distributed in the population. If this is the case and the sample size is not more than 30, researchers often use the t-model if the sample is not strongly skewed and does not have outliers.

Step 3: Assess the evidence.

• If a t-model is appropriate, determine the t-test statistic for the data’s sample mean.

[latex]\frac{\mathrm{sample}\text{}\mathrm{mean}-\mathrm{population}\text{}\mathrm{mean}}{\mathrm{estimated}\text{}\mathrm{standard}\text{}\mathrm{error}}\text{}=\text{}\frac{\stackrel{¯}{x}-μ}{s/\sqrt{n}}[/latex]

• Use the test statistic, together with the alternative hypothesis, to determine the P-value.

• The P-value is the probability of finding a random sample with a mean at least as extreme as our sample mean, assuming that the null hypothesis is true.

• As in all hypothesis tests, if the alternative hypothesis is greater than, the P-value is the area to the right of the test statistic. If the alternative hypothesis is less than, the P-value is the area to the left of the test statistic. If the alternative hypothesis is not equal to, the P-value is equal to double the tail area beyond the test statistic.

Step 4: Give the conclusion.

The logic of the hypothesis test is always the same. To state a conclusion about H₀, we compare the P-value to the significance level, α.

• If P ≤ α, we reject H₀. We conclude there is significant evidence in favor of H_a.
• If P > α, we fail to reject H₀. We conclude the sample does not provide significant evidence in favor of H_a.

• We write the conclusion in the context of the research question. Our conclusion is usually a statement about the alternative hypothesis (we accept H_a or fail to acceptH_a) and should include the P-value.

Other Hypothesis Testing Notes

• Remember that the P-value is the probability of seeing a sample mean at least as extreme as the one from the data if the null hypothesis is true. The probability is about the random sample; it is not a “chance” statement about the null or alternative hypothesis.

• Hypothesis tests are based on probability, so there is always a chance that the data has led us to make an error.
  • If our test results in rejecting a null hypothesis that is actually true, then it is called a type I error.
  • If our test results in failing to reject a null hypothesis that is actually false, then it is called a type II error.
  • If rejecting a null hypothesis would be very expensive, controversial, or dangerous, then we really want to avoid a type I error. In this case, we would set a strict significance level (a small value of α, such as 0.01).
• Finally, remember the phrase “garbage in, garbage out.” If the data collection methods are poor, then the results of a hypothesis test are meaningless.