Chapter 6: Linear Equations in Two Variables

6.3.1: Graphing Linear Equations in Two Variables

Learning Outcomes

  • Plot linear equations in two variables on the coordinate plane.
  • Use intercepts to plot lines.
  • Use a graphing utility to graph a linear equation on a coordinate plane.

Key words

  • Graph in two variables: a graph on a 2-dimensional plane
  • [latex]x[/latex]-intercept: the point where the graph crosses the [latex]x[/latex]-axis
  • [latex]y[/latex]-intercept: the point where the graph crosses the [latex]y[/latex]-axis

Graphing Linear Equations

Using Points to Plot Linear Equations

To graph a linear equation in two variables, we can plot a set of ordered pair solutions as points on a rectangular coordinate system. Its graph is called a graph in two variables. Any graph on a two-dimensional plane is a graph in two variables.

Suppose we want to graph the equation [latex]y=2x - 1[/latex]. We can begin by finding solutions for the equation by substituting values for [latex]x[/latex] into the equation and determining the resulting value of [latex]y[/latex]. Each pair of [latex]x[/latex] and [latex]y[/latex]-values is an ordered pair that can be plotted. The table below lists values of [latex]x[/latex] from –3 to 3 and the resulting values for [latex]y[/latex].

[latex]x[/latex] [latex]y=2x - 1[/latex] [latex]\left(x,y\right)[/latex]
[latex]-3[/latex] [latex]y=2\left(-3\right)-1=-7[/latex] [latex]\left(-3,-7\right)[/latex]
[latex]-2[/latex] [latex]y=2\left(-2\right)-1=-5[/latex] [latex]\left(-2,-5\right)[/latex]
[latex]-1[/latex] [latex]y=2\left(-1\right)-1=-3[/latex] [latex]\left(-1,-3\right)[/latex]
[latex]0[/latex] [latex]y=2\left(0\right)-1=-1[/latex] [latex]\left(0,-1\right)[/latex]
[latex]1[/latex] [latex]y=2\left(1\right)-1=1[/latex] [latex]\left(1,1\right)[/latex]
[latex]2[/latex] [latex]y=2\left(2\right)-1=3[/latex] [latex]\left(2,3\right)[/latex]
[latex]3[/latex] [latex]y=2\left(3\right)-1=5[/latex] [latex]\left(3,5\right)[/latex]

When we plot the points in the table, they form a line, so we can connect them.

This is not true for all equations, but the graph of a linear equation is always a line.

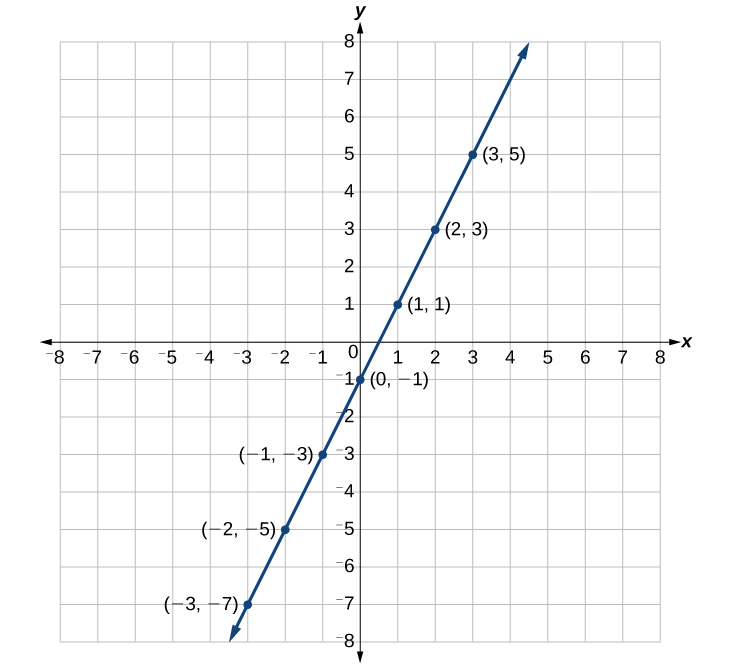
This is a graph of a line on an x, y coordinate plane. The x- and y-axis range from negative 8 to 8. A line passes through the points (-3, -7); (-2, -5); (-1, -3); (0, -1); (1, 1); (2, 3); and (3, 5).

Note that the [latex]x[/latex]–values chosen are arbitrary regardless of the type of equation we are graphing. Of course, some situations may require particular values of [latex]x[/latex] to be plotted in order to see a particular result. Otherwise, it is logical to choose values that can be calculated easily, and it is always a good idea to choose values that are both negative and positive. There is no rule dictating how many points to plot, although we need at least 2 to graph a line and at least 3 to guarantee the line is correct. Keep in mind, however, that the more points we plot, the more accurately we can sketch the graph.

How To graph a linear equation

  1. Make a solutions table.
  2. Plot the ordered pairs on a rectangular coordinate system.
  3. Connect the points if they form a line.

Example

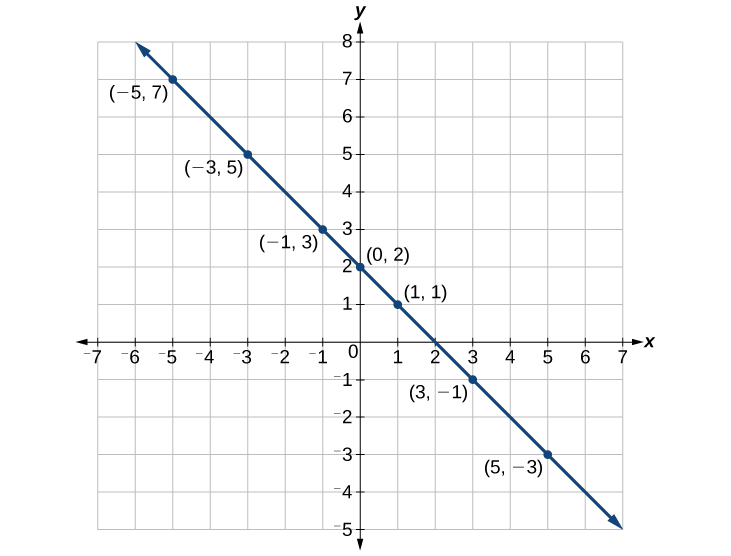
Graph the equation [latex]y=-x+2[/latex] by plotting points.

Solution

First, we construct a table by choosing [latex]x[/latex]-values and calculating the corresponding [latex]y[/latex]-values.

[latex]x[/latex] [latex]y=-x+2[/latex] [latex]\left(x,y\right)[/latex]
[latex]-5[/latex] [latex]y=-\left(-5\right)+2=7[/latex] [latex]\left(-5,7\right)[/latex]
[latex]-3[/latex] [latex]y=-\left(-3\right)+2=5[/latex] [latex]\left(-3,5\right)[/latex]
[latex]-1[/latex] [latex]y=-\left(-1\right)+2=3[/latex] [latex]\left(-1,3\right)[/latex]
[latex]0[/latex] [latex]y=-\left(0\right)+2=2[/latex] [latex]\left(0,2\right)[/latex]
[latex]1[/latex] [latex]y=-\left(1\right)+2=1[/latex] [latex]\left(1,1\right)[/latex]
[latex]3[/latex] [latex]y=-\left(3\right)+2=-1[/latex] [latex]\left(3,-1\right)[/latex]
[latex]5[/latex] [latex]y=-\left(5\right)+2=-3[/latex] [latex]\left(5,-3\right)[/latex]

Now, plot the points. Connect them since they form a line.

This image is a graph of a line on an x, y coordinate plane. The x-axis includes numbers that range from negative 7 to 7. The y-axis includes numbers that range from negative 5 to 8. A line passes through the points: (-5, 7); (-3, 5); (-1, 3); (0, 2); (1, 1); (3, -1); and (5, -3).

Try It

Construct a table and graph the equation by plotting points: [latex]y=\frac{1}{2}x+2[/latex].

TRY IT

Using Intercepts to Plot Linear Equations

The intercepts of a graph are points where the graph crosses the axes. The [latex]{x}[/latex]-intercept is the point where the graph crosses the [latex]x[/latex]–axis. At this point, the [latex]y[/latex]–coordinate is zero. The The [latex]{y}[/latex]–intercept is the point where the graph crosses the [latex]y[/latex]–axis. At this point, the [latex]x[/latex]–coordinate is zero.

INTERCEPTS

The [latex]x[/latex]-intercept is the point where the graph crosses the [latex]x[/latex]-axis. At this point [latex]y=0[/latex].

The [latex]y[/latex]-intercept is the point where the graph crosses the [latex]y[/latex]-axis. At this point [latex]x=0[/latex].

To determine the [latex]x[/latex]–intercept, we set [latex]y[/latex] equal to zero and solve for [latex]x[/latex]. Similarly, to determine the [latex]y[/latex]–intercept, we set [latex]x[/latex] equal to zero and solve for [latex]y[/latex]. For example, let’s find the intercepts of the equation [latex]y=3x - 1[/latex].

To find the [latex]x[/latex]–intercept, set [latex]y=0[/latex].

[latex]\begin{array}{llllll}y=3x - 1\hfill & \hfill \\ 0=3x - 1\hfill & \hfill \\ 1=3x\hfill & \hfill \\ \frac{1}{3}=x\hfill & \hfill \\ \left(\frac{1}{3},0\right)\hfill & x\text{-intercept}\hfill \end{array}[/latex]

To find the [latex]y[/latex]–intercept, set [latex]x=0[/latex].

[latex]\begin{array}{lllll}y=3x - 1\hfill & \hfill \\ y=3\left(0\right)-1\hfill & \hfill \\ y=-1\hfill & \hfill \\ \left(0,-1\right)\hfill & y\text{-intercept}\hfill \end{array}[/latex]

 

We can confirm that our results make sense by looking at a graph of the equation. Notice that the graph crosses the axes where we predicted it would.

This is an image of a line graph on an x, y coordinate plane. The x and y-axis range from negative 4 to 4. The function y = 3x – 1 is plotted on the coordinate plane

Example

Find the intercepts of the equation [latex]y=-3x - 4[/latex]. Then sketch the graph using only the intercepts. Verify your graph by determining another point on the line.

Solution

Set [latex]y=0[/latex] to find the [latex]x[/latex]-intercept.

[latex]\begin{array}{l}y=-3x - 4\hfill \\ 0=-3x - 4\hfill \\ 4=-3x\hfill \\ -\frac{4}{3}=x\hfill \\ \left(-\frac{4}{3},0\right)x\text{-intercept}\hfill \end{array}[/latex]

 

Set [latex]x=0[/latex] to find the [latex]y[/latex]-intercept.

[latex]\begin{array}{l}y=-3x - 4\hfill \\ y=-3\left(0\right)-4\hfill \\ y=-4\hfill \\ \left(0,-4\right)y\text{-intercept}\hfill \end{array}[/latex]

 

Plot both points and draw a line passing through them.

This is an image of a line graph on an x, y coordinate plane. The x-axis ranges from negative 5 to 5. The y-axis ranges from negative 6 to 3. The line passes through the points (-4/3, 0) and (0, -4).
We can check our line by finding a third point: choose [latex]x-1[/latex], then [latex]\begin{equation}\begin{aligned}y & =-3x - 4\\y & =-3(-1)-4\\y &=-1\end{aligned}\end{equation}[/latex].
The point [latex]\left (1, 1\right )[/latex] lies on the graph so we know we have the correct line.

Try It

Using a Graphing Utility to Plot Equations

We can use an online graphing tool to quickly plot lines. Watch this short video Tutorial to learn how.

Try It

Desmos has a helpful feature that allows us to turn a constant (number) into a variable. Follow these steps to learn how:

  1. Graph the line [latex]y=-\frac{2}{3}x-\frac{4}{3}[/latex].
  2. On the next line enter [latex]y=-a x-\frac{4}{3}[/latex]. You will see a button pop up that says “add slider: a”, click on the button. You will see the next line populated with the variable a and the interval on which a can take values.
  3. What part of a line does the variable a represent? The slope or the y-intercept?


Here is a short tutorial with more information about sliders.

 

 

Privacy Policy