Learning Outcomes
- Determine whether lines are parallel or perpendicular given their equations
- Find equations of lines that are parallel or perpendicular to a given line
The two lines in the graph below are parallel lines: they will never intersect. Notice that they have exactly the same steepness which means their slopes are identical. The only difference between the two lines is the y-intercept. If we shifted one line vertically toward the y-intercept of the other, they would become the same line.
Parallel lines.
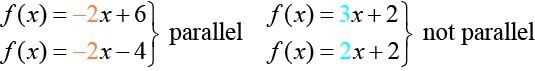
We can determine from their equations whether two lines are parallel by comparing their slopes. If the slopes are the same and the y-intercepts are different, the lines are parallel. If the slopes are different, the lines are not parallel.
Unlike parallel lines, perpendicular lines do intersect. Their intersection forms a right or 90-degree angle. The two lines below are perpendicular.
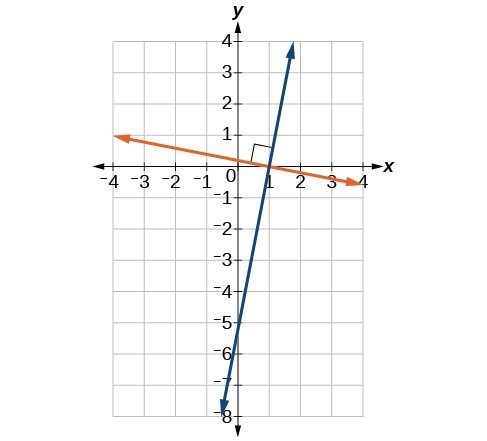
Perpendicular lines.
Perpendicular lines do not have the same slope. The slopes of perpendicular lines are different from one another in a specific way. The slope of one line is the negative reciprocal of the slope of the other line. The product of a number and its reciprocal is 1. If [latex]{m}_{1}\text{ and }{m}_{2}[/latex] are negative reciprocals of one another, they can be multiplied together to yield [latex]-1[/latex].
[latex]{m}_{1}*{m}_{2}=-1[/latex]
To find the reciprocal of a number, divide 1 by the number. So the reciprocal of 8 is [latex]\frac{1}{8}[/latex], and the reciprocal of [latex]\frac{1}{8}[/latex] is 8. To find the negative reciprocal, first find the reciprocal and then change the sign.
As with parallel lines, we can determine whether two lines are perpendicular by comparing their slopes. The slope of each line below is the negative reciprocal of the other so the lines are perpendicular.
[latex]\begin{array}{ll}f\left(x\right)=\frac{1}{4}x+2\hfill & \text{negative reciprocal of }\frac{1}{4}\text{ is }-4\hfill \\ f\left(x\right)=-4x+3\hfill & \text{negative reciprocal of }-4\text{ is }\frac{1}{4}\hfill \end{array}[/latex]
The product of the slopes is –1.
[latex]-4\left(\frac{1}{4}\right)=-1[/latex]
A General Note: Parallel and Perpendicular Lines
Two lines are parallel lines if they do not intersect. The slopes of the lines are the same.
[latex]f\left(x\right)={m}_{1}x+{b}_{1}\text{ and }g\left(x\right)={m}_{2}x+{b}_{2}\text{ are parallel if }{m}_{1}={m}_{2}[/latex].
If and only if [latex]{b}_{1}={b}_{2}[/latex] and [latex]{m}_{1}={m}_{2}[/latex], we say the lines coincide. Coincident lines are the same line.
Two lines are perpendicular lines if they intersect at right angles.
[latex]f\left(x\right)={m}_{1}x+{b}_{1}\text{ and }g\left(x\right)={m}_{2}x+{b}_{2}\text{ are perpendicular if }{m}_{1}*{m}_{2}=-1,\text{ and }{m}_{2}=-\frac{1}{{m}_{1}}[/latex].
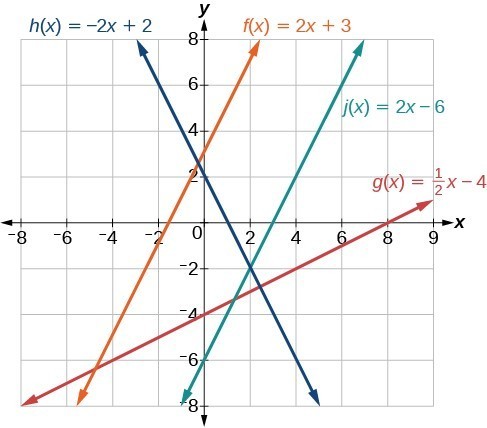
Example: Identifying Parallel and Perpendicular Lines
Given the functions below, identify the functions whose graphs are a pair of parallel lines and a pair of perpendicular lines.
[latex]\begin{array}{l}f\left(x\right)=2x+3\hfill & \hfill & h\left(x\right)=-2x+2\hfill \\ g\left(x\right)=\frac{1}{2}x - 4\hfill & \hfill & j\left(x\right)=2x - 6\hfill \end{array}[/latex]
Writing Equations of Parallel Lines
If we know the equation of a line, we can use what we know about slope to write the equation of a line that is either parallel or perpendicular to the given line.
Suppose we are given the following function:
[latex]f\left(x\right)=3x+1[/latex]
We know that the slope of the line is 3. We also know that the y-intercept is (0, 1). Any other line with a slope of 3 will be parallel to f(x). The lines formed by all of the following functions will be parallel to f(x).
[latex]\begin{array}{l}g\left(x\right)=3x+6\hfill \\ h\left(x\right)=3x+1\hfill \\ p\left(x\right)=3x+\frac{2}{3}\hfill \end{array}[/latex]
Suppose then we want to write the equation of a line that is parallel to f and passes through the point (1, 7). We already know that the slope is 3. We just need to determine which value for b will give the correct line. We can begin by using point-slope form of an equation for a line. We can then rewrite it in slope-intercept form.
[latex]\begin{array}{l}y-{y}_{1}=m\left(x-{x}_{1}\right)\hfill \\ y - 7=3\left(x - 1\right)\hfill \\ y - 7=3x - 3\hfill \\ \text{}y=3x+4\hfill \end{array}[/latex]
So [latex]g\left(x\right)=3x+4[/latex] is parallel to [latex]f\left(x\right)=3x+1[/latex] and passes through the point (1, 7).
How To: Given the equation of a linear function, write the equation of a line WHICH passes through a given point and is parallel to the given line.
- Find the slope of the function.
- Substitute the slope and given point into point-slope or slope-intercept form.
- Simplify.
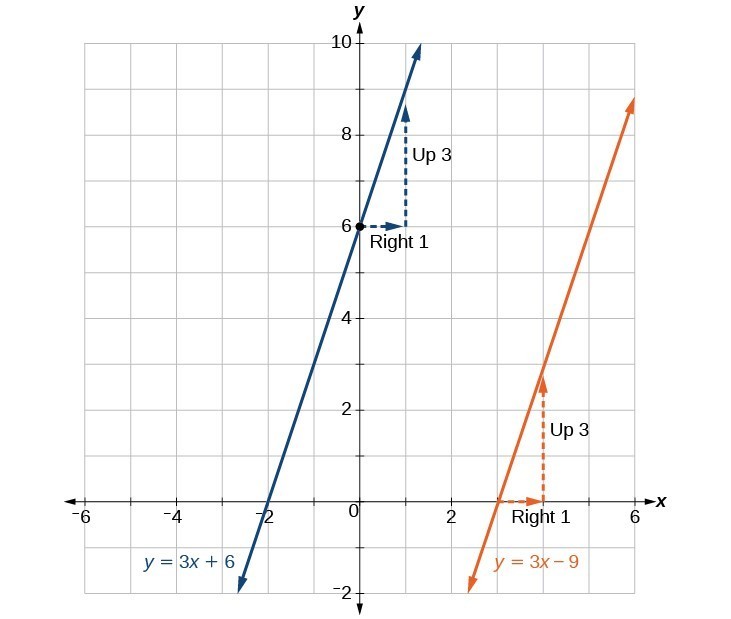
Example: Finding a Line Parallel to a Given Line
Find a line parallel to the graph of [latex]f\left(x\right)=3x+6[/latex] that passes through the point (3, 0).
Writing Equations of Perpendicular Lines
We can use a very similar process to write the equation of a line perpendicular to a given line. Instead of using the same slope, however, we use the negative reciprocal of the given slope. Suppose we are given the following function:
[latex]f\left(x\right)=2x+4[/latex]
The slope of the line is 2, and its negative reciprocal is [latex]-\frac{1}{2}[/latex]. Any function with a slope of [latex]-\frac{1}{2}[/latex] will be perpendicular to f(x). The lines formed by all of the following functions will be perpendicular to f(x).
[latex]\begin{array}{l}g\left(x\right)=-\frac{1}{2}x+4\hfill \\ h\left(x\right)=-\frac{1}{2}x+2\hfill \\ p\left(x\right)=-\frac{1}{2}x-\frac{1}{2}\hfill \end{array}[/latex]
As before, we can narrow down our choices for a particular perpendicular line if we know that it passes through a given point. Suppose that we want to write the equation of a line that is perpendicular to f(x) and passes through the point (4, 0). We already know that the slope is [latex]-\frac{1}{2}[/latex]. Now we can use the point to find the y-intercept by substituting the given values into the slope-intercept form of a line and solving for b.
[latex]\begin{array}{l}g\left(x\right)=mx+b\hfill \\ 0=-\frac{1}{2}\left(4\right)+b\hfill \\ 0=-2+b\hfill \\ 2=b\hfill \\ b=2\hfill \end{array}[/latex]
The equation for the function with a slope of [latex]-\frac{1}{2}[/latex] and a y-intercept of 2 is
[latex]g\left(x\right)=-\frac{1}{2}x+2[/latex].
So [latex]g\left(x\right)=-\frac{1}{2}x+2[/latex] is perpendicular to [latex]f\left(x\right)=2x+4[/latex] and passes through the point (4, 0). Be aware that perpendicular lines may not look obviously perpendicular on a graphing calculator unless we use the square zoom feature.
Q & A
A horizontal line has a slope of zero and a vertical line has an undefined slope. These two lines are perpendicular, but the product of their slopes is not –1. Doesn’t this fact contradict the definition of perpendicular lines?
No. For two perpendicular linear functions, the product of their slopes is –1. However, a vertical line is not a function so the definition is not contradicted.
How To: Given the equation of a linear function, write the equation of a line WHICH passes through a given point and is Perpendicular to the given line.
- Find the slope of the given function.
- Determine the negative reciprocal of the slope.
- Substitute the new slope and the values for x and y from given point into [latex]g\left(x\right)=mx+b[/latex].
- Solve for b.
- Write the equation of the line.
Example: Finding the Equation of a Perpendicular Line
Find the equation of a line perpendicular to [latex]f\left(x\right)=3x+3[/latex] that passes through the point (3, 0).
How To: Given two points on a line and a third point, write the equation of the perpendicular line that passes through the point.
- Determine the slope of the line passing through the points.
- Find the negative reciprocal of the slope.
- Use slope-intercept form or point-slope form to write the equation by substituting the known values.
- Simplify.
Example: Finding the Equation of a Line going through a point and Perpendicular to a Given Line
A line passes through the points (–2, 6) and (4, 5). Find the equation of a line that is perpendicular and passes through the point (4, 5).
Try It
A line passes through the points, (–2, –15) and (2, –3). Find the equation of a perpendicular line that passes through the point, (6, 4).