We previously wrote the equation for a linear function from a graph. Now we can extend what we know about graphing linear functions to analyze graphs a little more closely. Begin by taking a look at the graph below. We can see right away that the graph crosses the y-axis at the point (0, 4), so this is the y-intercept.

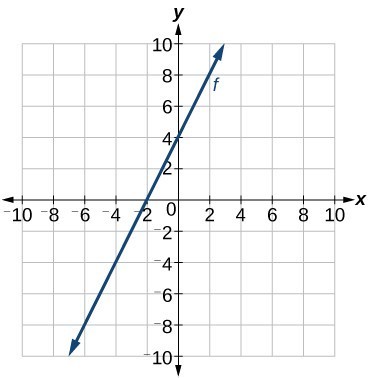
Then we can calculate the slope by finding the rise and run. We can choose any two points, but let’s look at the point (–2, 0). To get from this point to the y-intercept, we must move up 4 units (rise) and to the right 2 units (run). So the slope must be:

[latex]m=\frac{\text{rise}}{\text{run}}=\frac{4}{2}=2[/latex]

Substituting the slope and y-intercept into slope-intercept form of a line gives:

[latex]y=2x+4[/latex]

Finding the x-intercept of a Line

So far we have been finding the y-intercepts of functions: the point at which the graph of a function crosses the y-axis. A function may also have an x-intercept, which is the x-coordinate of the point where the graph of a function crosses the x-axis. In other words, it is the input value when the output value is zero.

To find the x-intercept, set the function f(x) equal to zero and solve for the value of x. For example, consider the function shown:

[latex]f\left(x\right)=3x - 6[/latex]

Set the function equal to 0 and solve for x.

[latex]\begin{array}{l}0=3x - 6\hfill \\ 6=3x\hfill \\ 2=x\hfill \\ x=2\hfill \end{array}[/latex]

The graph of the function crosses the x-axis at the point (2, 0).

Example: Finding an x-intercept

Find the x-intercept of [latex]f\left(x\right)=\frac{1}{2}x - 3[/latex].

Show Solution

Set the function equal to zero to solve for x.

[latex]\begin{array}{l}0=\frac{1}{2}x - 3\\ 3=\frac{1}{2}x\\ 6=x\\ x=6\end{array}[/latex]

The graph crosses the x-axis at the point (6, 0).

Analysis of the Solution

A graph of the function is shown below. We can see that the x-intercept is (6, 0) as expected.

The graph of the linear function [latex]f\left(x\right)=\frac{1}{2}x - 3[/latex].

 

Describing Horizontal and Vertical Lines

There are two special cases of lines on a graph—horizontal and vertical lines. A horizontal line indicates a constant output or y-value. In the graph below, we see that the output has a value of 2 for every input value. The change in outputs between any two points is 0. In the slope formula, the numerator is 0, so the slope is 0. If we use m = 0 in the equation [latex]f\left(x\right)=mx+b[/latex], the equation simplifies to [latex]f\left(x\right)=b[/latex]. In other words, the value of the function is a constant. This graph represents the function [latex]f\left(x\right)=2[/latex].

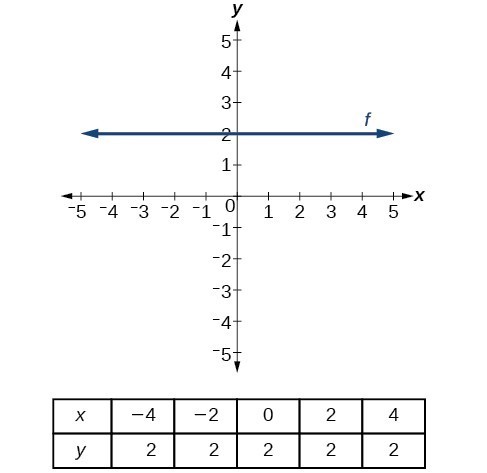
A horizontal line representing the function [latex]f\left(x\right)=2[/latex].

A vertical line indicates a constant input or x-value. We can see that the input value for every point on the line is 2, but the output value varies. Because this input value is mapped to more than one output value, a vertical line does not represent a function. Notice that between any two points, the change in the input values is zero. In the slope formula, the denominator will be zero, so the slope of a vertical line is undefined.

Notice that a vertical line has an x-intercept but no y-intercept unless it’s the line x = 0. This graph represents the line x = 2.

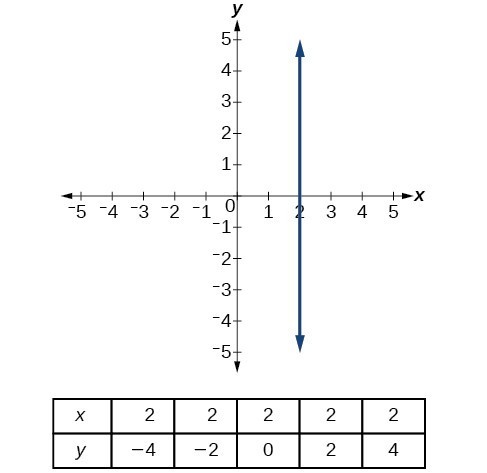
The vertical line [latex]x=2[/latex] which does not represent a function.

Contribute!

Improve this pageLearn More