Solve Systems of Three Equations in Three Variables

Learning Outcomes

Determine whether an ordered triple is a solution to a system of three equations.
Use back substitution to find a solution to a system of three equations.
Write the equations for a system given a scenario, and solve.

In order to solve systems of equations in three variables, known as three-by-three systems, the primary goal is to eliminate one variable at a time to achieve back-substitution. A solution to a system of three equations in three variables [latex]\left(x,y,z\right),\text{}[/latex] is called an ordered triple.

To find a solution, we can perform the following operations:

Interchange the order of any two equations.
Multiply both sides of an equation by a nonzero constant.
Add a nonzero multiple of one equation to another equation.

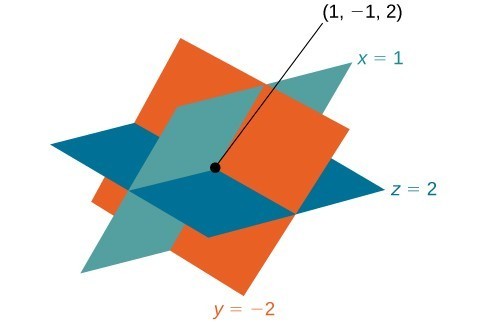
Graphically, the ordered triple defines the point that is the intersection of three planes in space. You can visualize such an intersection by imagining any corner in a rectangular room. A corner is defined by three planes: two adjoining walls and the floor (or ceiling). Any point where two walls and the floor meet represents the intersection of three planes.

A General Note: Number of Possible Solutions

The planes illustrate possible solution scenarios for three-by-three systems.

Systems that have a single solution are those which, after elimination, result in a solution set consisting of an ordered triple [latex]\left\{\left(x,y,z\right)\right\}[/latex]. Graphically, the ordered triple defines a point that is the intersection of three planes in space.
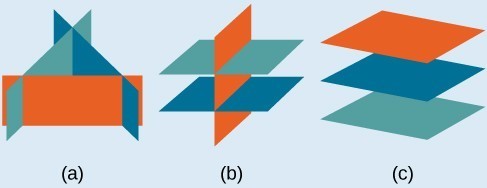
Systems that have an infinite number of solutions are those which, after elimination, result in an expression that is always true, such as [latex]0=0[/latex]. Graphically, an infinite number of solutions represents a line or coincident plane that serves as the intersection of three planes in space.
Systems that have no solution are those that, after elimination, result in a statement that is a contradiction, such as [latex]3=0[/latex]. Graphically, a system with no solution is represented by three planes with no point in common.

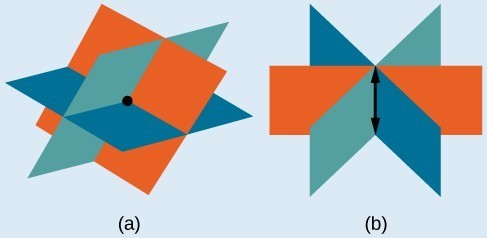
(a)Three planes intersect at a single point, representing a three-by-three system with a single solution. (b) Three planes intersect in a line, representing a three-by-three system with infinite solutions.

Example: Determining Whether an Ordered Triple Is a Solution to a System

Determine whether the ordered triple [latex]\left(3,-2,1\right)[/latex] is a solution to the system.

[latex]\begin{array}{l}\text{ }x+y+z=2\hfill \\ 6x - 4y+5z=31\hfill \\ 5x+2y+2z=13\hfill \end{array}[/latex]

Show Solution

How To: Given a linear system of three equations, solve for three unknowns.

Pick any pair of equations and solve for one variable.
Pick another pair of equations and solve for the same variable.
You have created a system of two equations in two unknowns. Solve the resulting two-by-two system.
Back-substitute known variables into any one of the original equations and solve for the missing variable.

Example: Solving a System of Three Equations in Three Variables by Elimination

Find a solution to the following system:

[latex]\begin{align}x - 2y+3z=9& &\text{(1)} \\ -x+3y-z=-6& &\text{(2)} \\ 2x - 5y+5z=17& &\text{(3)} \end{align}[/latex]

Show Solution

Try It

Solve the system of equations in three variables.

[latex]\begin{array}{l}2x+y - 2z=-1\hfill \\ 3x - 3y-z=5\hfill \\ x - 2y+3z=6\hfill \end{array}[/latex]

Show Solution

In the following video, you will see a visual representation of the three possible outcomes for solutions to a system of equations in three variables. There is also a worked example of solving a system using elimination.

Example: Solving a Real-World Problem Using a System of Three Equations in Three Variables

In the problem posed at the beginning of the section, John invested his inheritance of $12,000 in three different funds: part in a money-market fund paying 3% interest annually; part in municipal bonds paying 4% annually; and the rest in mutual funds paying 7% annually. John invested $4,000 more in mutual funds than he invested in municipal bonds. The total interest earned in one year was $670. How much did he invest in each type of fund?

Show Solution

To solve this problem, we use all of the information given and set up three equations. First, we assign a variable to each of the three investment amounts:

[latex]\begin{align}&x=\text{amount invested in money-market fund} \\ &y=\text{amount invested in municipal bonds} \\ z&=\text{amount invested in mutual funds} \end{align}[/latex]

The first equation indicates that the sum of the three principal amounts is $12,000.

[latex]x+y+z=12{,}000[/latex]

We form the second equation according to the information that John invested $4,000 more in mutual funds than he invested in municipal bonds.

[latex]z=y+4{,}000[/latex]

The third equation shows that the total amount of interest earned from each fund equals $670.

[latex]0.03x+0.04y+0.07z=670[/latex]

Then, we write the three equations as a system.

[latex]\begin{align}x+y+z=12{,}000 \\ -y+z=4{,}000 \\ 0.03x+0.04y+0.07z=670 \end{align}[/latex]

To make the calculations simpler, we can multiply the third equation by 100. Thus,

[latex]\begin{align}x+y+z=12{,}000 \hspace{5mm} \left(1\right) \\ -y+z=4{,}000 \hspace{5mm} \left(2\right) \\ 3x+4y+7z=67{,}000 \hspace{5mm} \left(3\right) \end{align}[/latex]

Step 1. Interchange equation (2) and equation (3) so that the two equations with three variables will line up.

[latex]\begin{align}x+y+z=12{,}000\hfill \\ 3x+4y +7z=67{,}000 \\ -y+z=4{,}000 \end{align}[/latex]

Step 2. Multiply equation (1) by [latex]-3[/latex] and add to equation (2). Write the result as row 2.

[latex]\begin{align}x+y+z=12{,}000 \\ y+4z=31{,}000 \\ -y+z=4{,}000 \end{align}[/latex]

Step 3. Add equation (2) to equation (3) and write the result as equation (3).

[latex]\begin{align}x+y+z=12{,}000 \\ y+4z=31{,}000 \\ 5z=35{,}000 \end{align}[/latex]

Step 4. Solve for [latex]z[/latex] in equation (3). Back-substitute that value in equation (2) and solve for [latex]y[/latex]. Then, back-substitute the values for [latex]z[/latex] and [latex]y[/latex] into equation (1) and solve for [latex]x[/latex].

[latex]\begin{align}&5z=35{,}000 \\ &z=7{,}000 \\ \\ &y+4\left(7{,}000\right)=31{,}000 \\ &y=3{,}000 \\ \\ &x+3{,}000+7{,}000=12{,}000 \\ &x=2{,}000 \end{align}[/latex]

John invested $2,000 in a money-market fund, $3,000 in municipal bonds, and $7,000 in mutual funds.

Try It

Contribute!

Did you have an idea for improving this content? We’d love your input.

Improve this page Learn More

Module 13: Systems of Equations and Inequalities