Learning Outcomes
- Find the domain of a square root and rational function
- Find the domain of a function from its algebraic form.
Functions are a correspondence between two sets, called the domain and the range. When defining a function, you usually state what kind of numbers the domain (x) and range (f(x)) values can be. But even if you say they are real numbers, that does not mean that all real numbers can be used for x. It also does not mean that all real numbers can be function values, f(x). There may be restrictions on the domain and range. The restrictions partly depend on the type of function.
In this topic, all functions will be restricted to real number values. That is, only real numbers can be used in the domain, and only real numbers can be in the range.
There are two main reasons why domains are restricted.
- You cannot divide by [latex]0[/latex].
- You cannot take the square (or other even) root of a negative number, as the result will not be a real number.
These two issues would be of concern when the function is either of the following:
- A rational function where the denominator could potentially become [latex]0[/latex] for some value or values of x, [latex]f\left(x\right)=\dfrac{x+1}{2-x}[/latex] is a rational function.
- A radical function with an even index (such as a square root), where the radicand (quantity under the radical) could potentially be negative for some value or values of x. [latex]f\left(x\right)=\sqrt{7-x}[/latex] is a radical function.
The following table gives examples of domain restrictions for several different rational functions. Note that a rational function has the variable present in the denominator.
| Function | Restrictions to the Domain |
|---|---|
| [latex]f(x)=\dfrac{1}{x}[/latex] | If [latex]x=0[/latex], you would be dividing by [latex]0[/latex], so [latex]x\neq0[/latex]. |
| [latex]f(x)=\dfrac{2+x}{x-3}[/latex] | If [latex]x=3[/latex], you would be dividing by [latex]0[/latex], so [latex]x\neq3[/latex]. |
| [latex]f(x)=\dfrac{2(x-1)}{x-1}[/latex] | Although you can simplify this function to [latex]f(x)=2[/latex], when [latex]x=1[/latex], the original function would include division by [latex]0[/latex], so [latex]x\neq1[/latex]. |
| [latex]f(x)=\dfrac{x+1}{{{x}^{2}}-1}[/latex] | Both [latex]x=1[/latex] and [latex]x=−1[/latex] would make the denominator 0. Again, this function can be simplified to [latex]f(x)=\dfrac{1}{x-1}[/latex], but when [latex]x=1[/latex] or [latex]x=−1[/latex], the original function would include division by 0, so [latex]x\neq1[/latex] and [latex]x\neq−1[/latex]. |
| [latex]f(x)=\dfrac{2(x-1)}{{{x}^{2}}+1}[/latex] | This is an example with no domain restrictions, even though there is a variable in the denominator. Since [latex]x^{2}\geq0,x^{2}+1[/latex] can never be [latex]0[/latex]. The least it can be is [latex]1[/latex], so there is no danger of division by [latex]0[/latex]. |
Square roots of negative numbers could happen whenever the function has a variable under a radical with an even root. Look at the following examples and note that “square root of a negative variable” doesn’t necessarily mean that the value under the radical sign is negative. For example, if [latex]x=−4[/latex], then [latex]−x=−(−4)=4[/latex], a positive number.
| Function | Restrictions to the Domain |
|---|---|
| [latex]f(x)=\sqrt{x}[/latex] | If [latex]x<0[/latex], you would be taking the square root of a negative number, so [latex]x\geq0[/latex]. |
| [latex]f(x)=\sqrt{x+10}[/latex] | If [latex]x<−10[/latex], you would be taking the square root of a negative number, so [latex]x\geq−10[/latex]. |
| [latex]f(x)=\sqrt{-x}[/latex] | When is [latex]-x[/latex] negative? Only when x is positive. (For example, if [latex]x=1[/latex], then [latex]−x=-1[/latex]. But if [latex]x=-3[/latex], then [latex]−x=3[/latex]. This means [latex]x\leq0[/latex]. |
| [latex]f(x)=\sqrt{{{x}^{2}}-1}[/latex] | [latex]x^{2}–1[/latex] must be positive, [latex]x^{2}–1>0[/latex]. So [latex]x^{2}>1[/latex]. This happens only when x is greater than 1 or less than [latex]−1[/latex]: [latex]x\leq−1[/latex] or [latex]x\geq1[/latex]. |
| [latex]f(x)=\sqrt{{{x}^{2}}+10}[/latex] | There are no domain restrictions even though there is a variable under the radical. Since [latex]x^{2}\ge0[/latex], [latex]x^{2}+10[/latex] can never be negative. The least it can be is [latex]\sqrt{10}[/latex], so there is no danger of taking the square root of a negative number. |
So, how exactly do you define the domain of a function?
How To: Given a function written in equation form, find the domain
- Identify the input values.
- Identify any restrictions on the input and exclude those values from the domain.
- Write the domain in interval form, if possible.
Example
Find the domain of the function [latex]f\left(x\right)={x}^{2}-1[/latex].
How To: Given a function written in equation form that includes a fraction, find the domain
- Identify the input values.
- Identify any restrictions on the input. If there is a denominator in the function’s formula, set the denominator equal to zero and solve for [latex]x[/latex] . If the function’s formula contains an even root, set the radicand greater than or equal to [latex]0[/latex] and then solve.
- Write the domain in interval form, making sure to exclude any restricted values from the domain.
Example
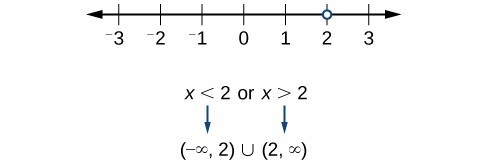
Find the domain of the function [latex]f\left(x\right)=\dfrac{x+1}{2-x}[/latex].
How To: Given a function written in equation form including an even root, find the domain
- Identify the input values.
- Since there is an even root, exclude any real numbers that result in a negative number in the radicand. Set the radicand greater than or equal to zero and solve for [latex]x[/latex].
- The solution(s) are the domain of the function. If possible, write the answer in interval form.
Example
Find the domain of the function [latex]f\left(x\right)=\sqrt{7-x}[/latex].
The domain and range of a function are not necessarily the same. For example, the function [latex]f\left(x\right)=-\dfrac{1}{\sqrt{x}}[/latex] has the set of all positive real numbers as its domain but the set of all negative real numbers as its range. As a more extreme example, a function’s inputs and outputs can be completely different categories (for example, names of weekdays as inputs and numbers as outputs, as on an attendance chart), in such cases the domain and range have no elements in common.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- College Algebra. Authored by: Jay Abramson, et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175. License: CC BY: Attribution. License Terms: Download for Free at: http://cnx.org/contents/fd53eae1-fa23-47c7-bb1b-972349835c3c@5.175
- Ex: The Domain of Rational Functions. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/v0IhvIzCc_I. License: CC BY: Attribution
- Ex. Domain and Range of Square Root Functions. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/lj_JB8sfyIM. License: CC BY: Attribution