Learning Outcome
- Define the domain of linear, quadratic, radical, and rational functions from graphs
Finding domain and range of different functions is often a matter of asking yourself, what values can this function not have? Pictures make it easier to visualize what the domain and range are, so we will show how to define the domain and range of functions given their graphs.
What are the domain and range of the real-valued function [latex]f(x)=x+3[/latex]?
This is a linear function. Remember that linear functions are lines that continue forever in each direction.
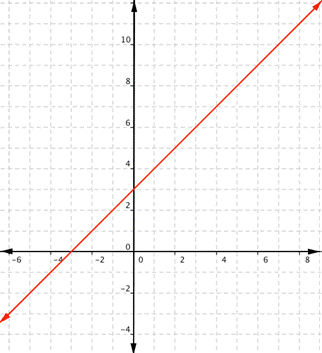
Any real number can be substituted for x and get a meaningful output. For any real number, you can always find an x value that gives you that number for the output. Unless a linear function is a constant, such as [latex]f(x)=2[/latex], there is no restriction on the range.
The domain and range are all real numbers.
For the examples that follow, try to figure out the domain and range of the graphs before you look at the answer.
Example
What are the domain and range of the real-valued function [latex]f(x)=−3x^{2}+6x+1[/latex]?
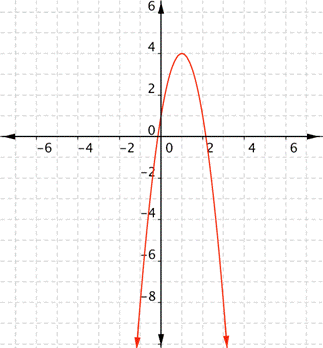
Example
What is the domain and range of the real-valued function [latex]f(x)=-2+\sqrt{x+5}[/latex]?
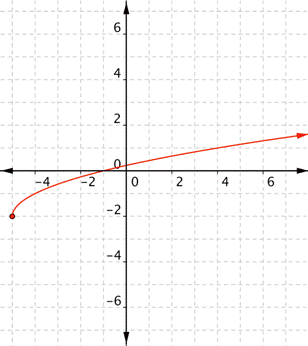
Example
What is the domain of the real-valued function [latex]\displaystyle f(x)=\frac{3x}{x+2}[/latex]?
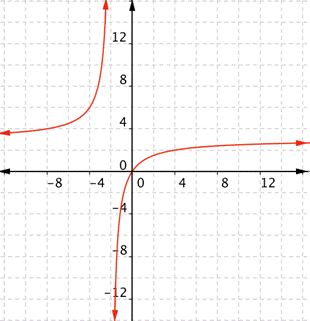
In the following video we show how to define the domain and range of functions from their graphs.
Summary
Although a function may be given as “real valued,” it may be that the function has restrictions to its domain and range. There may be some real numbers that cannot be part of the domain or part of the range. This is particularly true with rational and radical functions which can have restrictions to their domain, range, or both. Other functions, such as quadratic functions and polynomial functions of even degree, can also have restrictions to their range.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex 1: Determine the Domain and Range of the Graph of a Function. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/QAxZEelInJc. License: CC BY: Attribution
- Unit 17: Functions, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
