Learning Outcomes
- Write a recursive formula given a sequence of numbers.
- Given two terms in a geometric sequence, find a third.
- Solve an application problem using a geometric sequence.
Using Recursive Formulas for Geometric Sequences
A recursive formula allows us to find any term of a geometric sequence by using the previous term. Each term is the product of the common ratio and the previous term. For example, suppose the common ratio is 9. Then each term is nine times the previous term. As with any recursive formula, the initial term must be given.
A General Note: Recursive Formula for a Geometric Sequence
The recursive formula for a geometric sequence with common ratio [latex]r[/latex] and first term [latex]{a}_{1}[/latex] is
[latex]{a}_{n}=r\cdot{a}_{n - 1},n\ge 2[/latex]
How To: Given the first several terms of a geometric sequence, write its recursive formula.
- State the initial term.
- Find the common ratio by dividing any term by the preceding term.
- Substitute the common ratio into the recursive formula for a geometric sequence.
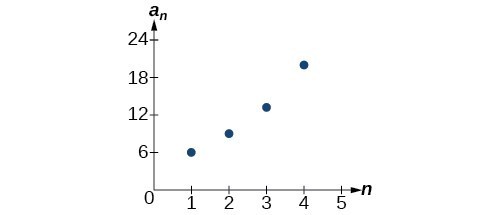
Example: Using Recursive Formulas for Geometric Sequences
Write a recursive formula for the following geometric sequence.
[latex]\left\{6,9,13.5,20.25,\dots\right\}[/latex]
Q & A
Do we have to divide the second term by the first term to find the common ratio?
No. We can divide any term in the sequence by the previous term. It is, however, most common to divide the second term by the first term because it is often the easiest method of finding the common ratio.
Try It
Write a recursive formula for the following geometric sequence.
[latex]\left\{2,\dfrac{4}{3},\dfrac{8}{9},\dfrac{16}{27},\dots\right\}[/latex]
Using Explicit Formulas for Geometric Sequences
Because a geometric sequence is an exponential function whose domain is the set of positive integers, and the common ratio is the base of the function, we can write explicit formulas that allow us to find particular terms.
[latex]{a}_{n}={a}_{1}{r}^{n - 1}[/latex]
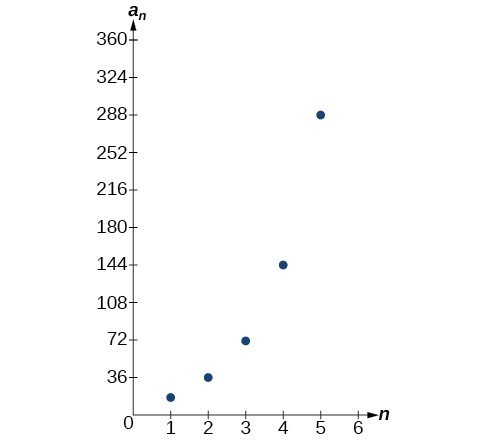
Let’s take a look at the sequence [latex]\left\{18\text{, }36\text{, }72\text{, }144\text{, }288\text{, }…\right\}[/latex]. This is a geometric sequence with a common ratio of 2 and an exponential function with a base of 2. An explicit formula for this sequence is
[latex]{a}_{n}=18\cdot {2}^{n - 1}[/latex]
A General Note: Explicit Formula for a Geometric Sequence
The nth term of a geometric sequence is given by the explicit formula:
[latex]{a}_{n}={a}_{1}{r}^{n - 1}[/latex]
Example: Writing Terms of Geometric Sequences Using the Explicit Formula
Given a geometric sequence with [latex]{a}_{1}=3[/latex] and [latex]{a}_{4}=24[/latex], find [latex]{a}_{2}[/latex].
Try It
Given a geometric sequence with [latex]{a}_{2}=4[/latex] and [latex]{a}_{3}=32[/latex] , find [latex]{a}_{6}[/latex].
https://ohm.lumenlearning.com/multiembedq.php?id=5856&theme=oea&iframe_resize_id=mom5
Example: Writing an Explicit Formula for the nth Term of a Geometric Sequence
Write an explicit formula for the [latex]n\text{th}[/latex] term of the following geometric sequence.
[latex]\left\{2,10,50,250,\dots\right\}[/latex]
Try It
Write an explicit formula for the following geometric sequence.
[latex]\left\{-1,3,-9,27,\dots\right\}[/latex]
https://ohm.lumenlearning.com/multiembedq.php?id=29756&theme=oea&iframe_resize_id=mom1
In real-world scenarios involving arithmetic sequences, we may need to use an initial term of [latex]{a}_{0}[/latex] instead of [latex]{a}_{1}[/latex]. In these problems we can alter the explicit formula slightly by using the following formula:
[latex]{a}_{n}={a}_{0}{r}^{n}[/latex]
recall exponential applications
You have solved problems such as the following before in Module 11: Exponential and Logarithmic Functions. Feel free to return to that material anytime for a refresher.
Example: Solving Application Problems with Geometric Sequences
In 2013, the number of students in a small school is 284. It is estimated that the student population will increase by 4% each year.
- Write a formula for the student population.
- Estimate the student population in 2020.
Try It
A business starts a new website. Initially the number of hits is 293 due to the curiosity factor. The business estimates the number of hits will increase by 2.6% per week.
- Write a formula for the number of hits.
- Estimate the number of hits in 5 weeks.
The following video provides a short lesson on some of the topics covered in this lesson.