Learning Outcomes
- Find the common ratio of a geometric sequence
- List terms of a geometric sequence given the first term and the common ratio
Finding Common Ratios
The yearly salary values described form a geometric sequence because they change by a constant factor each year. Each term of a geometric sequence increases or decreases by a constant factor called the common ratio. The sequence below is an example of a geometric sequence because each term increases by a constant factor of 6. Multiplying any term of the sequence by the common ratio 6 generates the subsequent term.

A General Note: Definition of a Geometric Sequence
A geometric sequence is one in which any term divided by the previous term is a constant. This constant is called the common ratio of the sequence. The common ratio can be found by dividing any term in the sequence by the previous term. If [latex]{a}_{1}[/latex] is the initial term of a geometric sequence and [latex]r[/latex] is the common ratio, the sequence will be
[latex]\left\{{a}_{1}, {a}_{1}r,{a}_{1}{r}^{2},{a}_{1}{r}^{3},…\right\}[/latex].
How To: Given a set of numbers, determine if they represent a geometric sequence.
- Divide each term by the previous term.
- Compare the quotients. If they are the same, a common ratio exists and the sequence is geometric.
Example: Finding Common Ratios
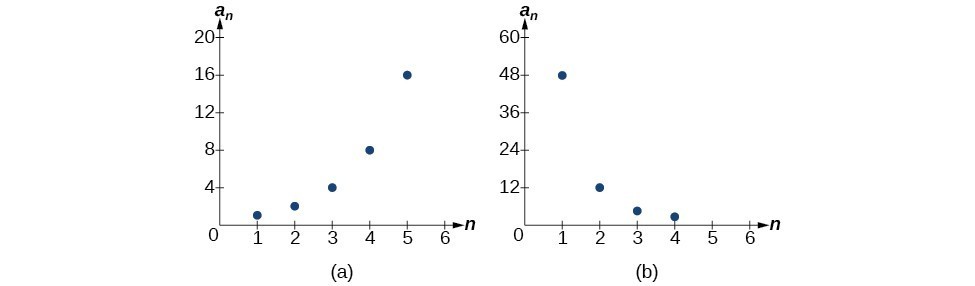
Is the sequence geometric? If so, find the common ratio.
- [latex]1,2,4,8,16,\dots[/latex]
- [latex]48,12,4,2,\dots[/latex]
Q & A
If you are told that a sequence is geometric, do you have to divide every term by the previous term to find the common ratio?
No. If you know that the sequence is geometric, you can choose any one term in the sequence and divide it by the previous term to find the common ratio.
Try It
Is the sequence geometric? If so, find the common ratio.
[latex]5,10,15,20,\dots[/latex]
https://ohm.lumenlearning.com/multiembedq.php?id=68722&theme=oea&iframe_resize_id=mom2
Try It
Is the sequence geometric? If so, find the common ratio.
[latex]100,20,4,\dfrac{4}{5},\dots[/latex]
Writing Terms of Geometric Sequences
Now that we can identify a geometric sequence, we will learn how to find the terms of a geometric sequence if we are given the first term and the common ratio. The terms of a geometric sequence can be found by beginning with the first term and multiplying by the common ratio repeatedly. For instance, if the first term of a geometric sequence is [latex]{a}_{1}=-2[/latex] and the common ratio is [latex]r=4[/latex], we can find subsequent terms by multiplying [latex]-2\cdot 4[/latex] to get [latex]-8[/latex] then multiplying the result [latex]-8\cdot 4[/latex] to get [latex]-32[/latex] and so on.
[latex]\begin{align}&{a}_{1}=-2 \\ &{a}_{2}=\left(-2\cdot 4\right)=-8 \\ &{a}_{3}=\left(-8\cdot 4\right)=-32 \\ &{a}_{4}=\left(-32\cdot 4\right)=-128 \end{align}[/latex]
The first four terms are [latex]\left\{-2,-8,-32,-128\right\}[/latex].
How To: Given the first term and the common factor, find the first four terms of a geometric sequence.
- Multiply the initial term, [latex]{a}_{1}[/latex], by the common ratio to find the next term, [latex]{a}_{2}[/latex].
- Repeat the process, using [latex]{a}_{n}={a}_{2}[/latex] to find [latex]{a}_{3}[/latex] and then [latex]{a}_{3}[/latex] to find [latex]{a}_{4,}[/latex] until all four terms have been identified.
- Write the terms separated by commons within brackets.
tip for success
You can also use the definition of a geometric sequence, given at the beginning of the section, to write out several terms.
[latex]\left\{{a}_{1}, {a}_{1}r,{a}_{1}{r}^{2},{a}_{1}{r}^{3},…\right\}[/latex]
Try it on the example and practice problems below.
Example: Writing the Terms of a Geometric Sequence
List the first four terms of the geometric sequence with [latex]{a}_{1}=5[/latex] and [latex]r=-2[/latex].
Try It
List the first five terms of the geometric sequence with [latex]{a}_{1}=18[/latex] and [latex]r=\dfrac{1}{3}[/latex].
https://ohm.lumenlearning.com/multiembedq.php?id=156689&theme=oea&iframe_resize_id=mom3