Learning Outcomes
- Find the [latex]y[/latex]-intercept of a quadratic function.
- Find the real-number [latex]x[/latex]-intercepts, or roots of a quadratic function using factoring and the quadratic formula.
Much as we did in the application problems above, we also need to find intercepts of quadratic equations for graphing parabolas. Recall that we find the [latex]y[/latex]-intercept of a quadratic by evaluating the function at an input of zero, and we find the [latex]x[/latex]-intercepts at locations where the output is zero. Notice that the number of [latex]x[/latex]-intercepts can vary depending upon the location of the graph.
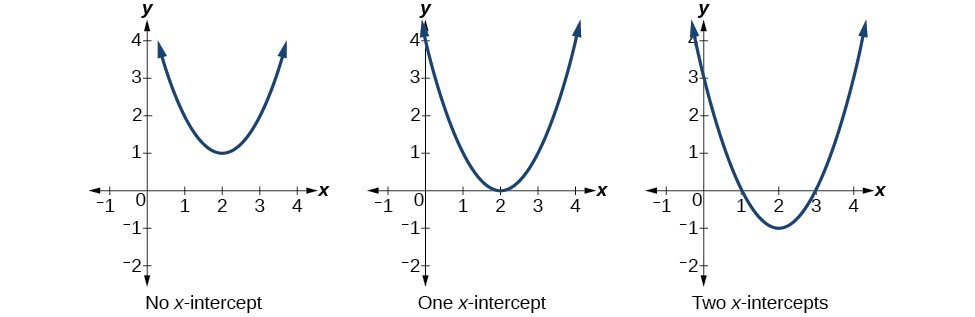
Number of [latex]x[/latex]-intercepts of a parabola
Tip for success
We’ve built up several names for the values where a function crosses the horizontal axis:
- horizontal intercepts or x-intercepts
- zeros
- roots
We tend to talk about intercepts with regard to a graph, zeros as solutions to an equation, and roots with regard to a function. Each term refers to the same value, though, for each quadratic function.
more
Ex. [latex]f(x)=x^2-x-12[/latex]
- The x-intercepts of the graph are located at [latex](-3, 0)[/latex] and [latex](4, 0)[/latex].
- The zeros of the equation [latex]0 = x^2-x-12[/latex] are [latex]-3[/latex] and [latex]4[/latex].
- The function[latex] f(x) = x^2 - x -12[/latex] has roots [latex]-3[/latex] and [latex]4[/latex].
How To: Given a quadratic function [latex]f\left(x\right)[/latex], find the y– and x-intercepts.
- Evaluate [latex]f\left(0\right)[/latex] to find the [latex]y[/latex]-intercept.
- Solve the quadratic equation [latex]f\left(x\right)=0[/latex] to find the [latex]x[/latex]-intercepts.
Example: Finding the y– and x-Intercepts of a Parabola
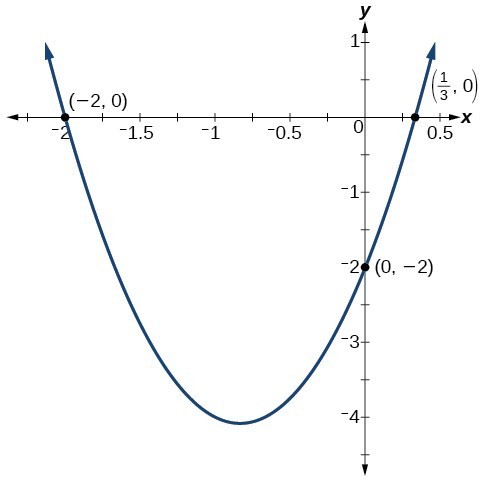
Find the [latex]y[/latex]– and [latex]x[/latex]-intercepts of the quadratic [latex]f\left(x\right)=3{x}^{2}+5x - 2[/latex].
Show Solution
We find the [latex]y[/latex]-intercept by evaluating [latex]f\left(0\right)[/latex].
[latex]f\left(0\right)=3{\left(0\right)}^{2}+5\left(0\right)-2=-2[/latex]
So the [latex]y[/latex]-intercept is at [latex]\left(0,-2\right)[/latex].
For the [latex]x[/latex]-intercepts, or roots, we find all solutions of [latex]f\left(x\right)=0[/latex].
[latex]3{x}^{2}+5x - 2=0[/latex]
In this case, the quadratic can be factored easily, providing the simplest method for solution.
[latex]\left(3x - 1\right)\left(x+2\right)=0[/latex]
[latex]\begin{align}&3x - 1=0&x+2=0\end{align}[/latex]
[latex]x=\frac{1}{3}\hspace{8mm}[/latex] or [latex]\hspace{8mm}x=-2[/latex]
So the roots are at [latex]\left(\frac{1}{3},0\right)[/latex] and [latex]\left(-2,0\right)[/latex].
Analysis of the Solution
By graphing the function, we can confirm that the graph crosses the [latex]y[/latex]-axis at [latex]\left(0,-2\right)[/latex]. We can also confirm that the graph crosses the [latex]x[/latex]-axis at [latex]\left(\frac{1}{3},0\right)[/latex] and [latex]\left(-2,0\right)[/latex].
In the above example the quadratic was easily solved by factoring. However, there are many quadratics that cannot be factored. We can solve these quadratics by first rewriting them in standard form.
How To: Given a quadratic function, find the x-intercepts by rewriting in standard form.
- Substitute [latex]a[/latex] and [latex]b[/latex] into [latex]h=-\dfrac{b}{2a}[/latex].
- Substitute [latex]x=h[/latex] into the general form of the quadratic function to find [latex]k[/latex].
- Rewrite the quadratic in standard form using [latex]h[/latex] and [latex]k[/latex].
- Solve for when the output of the function will be zero to find the [latex]x[/latex]–intercepts.
Example: Finding the Roots of a Parabola
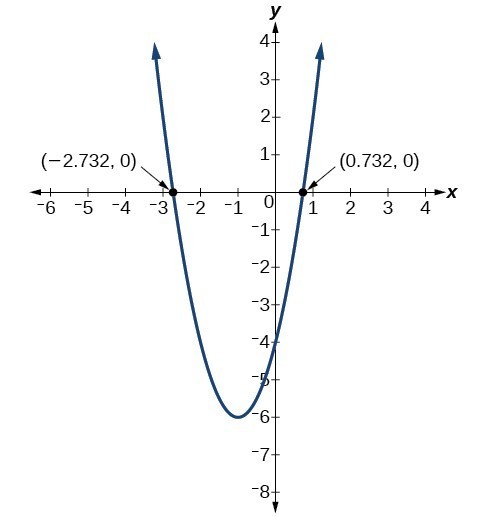
Find the [latex]x[/latex]-intercepts of the quadratic function [latex]f\left(x\right)=2{x}^{2}+4x - 4[/latex].
Show Solution
We begin by solving for when the output will be zero.
[latex]0=2{x}^{2}+4x - 4[/latex]
Because the quadratic is not easily factorable in this case, we solve for the intercepts by first rewriting the quadratic in standard form.
[latex]f\left(x\right)=a{\left(x-h\right)}^{2}+k[/latex]
We know that [latex]a=2[/latex]. Then we solve for [latex]h[/latex] and [latex]k[/latex].
[latex]\begin{align}&h=-\dfrac{b}{2a}=-\dfrac{4}{2\left(2\right)}=-1\\[1mm]&\end{align}[/latex]
[latex]\begin{align}k&=f\left(h\right)\\&=f\left(-1\right)\\&=2{\left(-1\right)}^{2}+4\left(-1\right)-4\\&=-6\end{align}[/latex]
So now we can rewrite in standard form.
[latex]f\left(x\right)=2{\left(x+1\right)}^{2}-6[/latex]
We can now solve for when the output will be zero.
[latex]\begin{align}&0=2{\left(x+1\right)}^{2}-6 \\ &6=2{\left(x+1\right)}^{2} \\ &3={\left(x+1\right)}^{2} \\ &x+1=\pm \sqrt{3} \\ &x=-1\pm \sqrt{3} \end{align}[/latex]
The graph has [latex]x[/latex]–intercepts at [latex]\left(-1-\sqrt{3},0\right)[/latex] and [latex]\left(-1+\sqrt{3},0\right)[/latex].
Analysis of the Solution
We can check our work by graphing the given function on a graphing utility and observing the roots.
Try It
Using an online graphing calculator, plot the function [latex]g\left(x\right)=-7+{x}^{2}-6x[/latex]. You can use this tool to find the [latex]x[/latex]-and [latex]y[/latex]-intercepts by clicking on the graph. Four points will appear. List each point, and what kind of point it is, we got you started with the vertex:
- Vertex = [latex](3,-16)[/latex]
Show Solution
[latex]y[/latex]-intercept at [latex](0, -7)[/latex]
[latex]x[/latex]-intercept at [latex](-1,0)[/latex]
[latex]x[/latex]-intercept at [latex](7,0)[/latex]
tip for success
When attempting to identify the roots of a quadratic function, first look to see if it can be factored when the function value is set equal to zero, and solved by applying the zero-product principle. If so, this is often the quickest method. But most quadratic functions cannot be factored. In this case, you can either write it in vertex form or use the quadratic formula.
more
1. The quadratic formula will reveal the x-intercepts of the graph of any quadratic equation.
[latex]x=\dfrac{-b \pm \sqrt{b^2-4ac}}{2a}[/latex]
2. The vertex formula will reveal the vertex of any parabola.
[latex]\left(\dfrac{-b}{2a}, f\left(\dfrac{-b}{2a}\right) \right)[/latex]
3. The y-intercept, often called the initial value, of the function can be found by setting the input variable to 0.
Evaluate the function at zero to find the y-intercept: [latex]f(0) = y[/latex]
These three pieces of information are of particular value when solving applications of quadratic functions.
Example: Solving a Quadratic Equation with the Quadratic Formula
Solve [latex]{x}^{2}+x+2=0[/latex].
Show Solution
Let’s begin by writing the quadratic formula: [latex]x=\dfrac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}[/latex].
When applying the quadratic formula, we identify the coefficients [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex]. For the equation [latex]{x}^{2}+x+2=0[/latex], we have [latex]a=1[/latex], [latex]b=1[/latex], and [latex]c=2[/latex]. Substituting these values into the formula we have:
[latex]\begin{align}x&=\dfrac{-b\pm \sqrt{{b}^{2}-4ac}}{2a} \\[1.5mm] &=\dfrac{-1\pm \sqrt{{1}^{2}-4\cdot 1\cdot \left(2\right)}}{2\cdot 1} \\[1.5mm] &=\dfrac{-1\pm \sqrt{1 - 8}}{2} \\[1.5mm] &=\dfrac{-1\pm \sqrt{-7}}{2} \\[1.5mm] &=\dfrac{-1\pm i\sqrt{7}}{2} \end{align}[/latex]
The solutions to the equation are [latex]x=\dfrac{-1+i\sqrt{7}}{2}[/latex] and [latex]x=\dfrac{-1-i\sqrt{7}}{2}[/latex] or [latex]x=-\dfrac{1}{2}+\dfrac{i\sqrt{7}}{2}[/latex] and [latex]x=-\dfrac{1}{2}-\dfrac{i\sqrt{7}}{2}[/latex].
Analysis of the Solution
This quadratic equation has only non-real solutions.
Example: Applying the Vertex and x-Intercepts of a Parabola
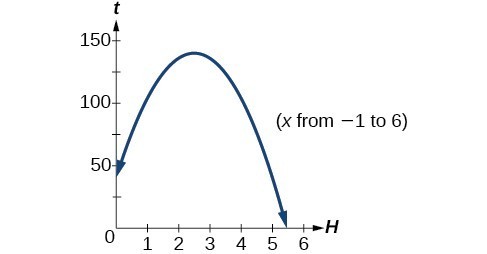
A ball is thrown upward from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+80t+40[/latex].
a. When does the ball reach the maximum height?
b. What is the maximum height of the ball?
c. When does the ball hit the ground?
Show Solution
a. The ball reaches the maximum height at the vertex of the parabola.
[latex]\begin{align}h&=-\dfrac{80}{2\left(-16\right)} \\[1mm]&=\dfrac{80}{32} \\[1mm] &=\dfrac{5}{2} \\[1mm] &=2.5 \end{align}[/latex]
The ball reaches a maximum height after 2.5 seconds.
b. To find the maximum height, find the [latex]y[/latex] coordinate of the vertex of the parabola.
[latex]\begin{align}k&=H\left(2.5\right) \\[1mm] &=-16{\left(2.5\right)}^{2}+80\left(2.5\right)+40 \\[1mm] &=140\hfill \end{align}[/latex]
The ball reaches a maximum height of 140 feet.
c. To find when the ball hits the ground, we need to determine when the height is zero, [latex]H\left(t\right)=0[/latex].
We use the quadratic formula.
[latex]\begin{align} t&=\dfrac{-80\pm \sqrt{{80}^{2}-4\left(-16\right)\left(40\right)}}{2\left(-16\right)} \\[1mm] &=\dfrac{-80\pm \sqrt{8960}}{-32} \end{align}[/latex]
Because the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions.
[latex]t=\dfrac{-80+\sqrt{8960}}{-32}\approx 5.458\hspace{3mm}[/latex] or [latex]\hspace{3mm}t=\dfrac{-80-\sqrt{8960}}{-32}\approx -0.458[/latex]
Since the domain starts at [latex]t=0[/latex] when the ball is thrown, the second answer is outside the reasonable domain of our model. The ball will hit the ground after about 5.46 seconds.
Try It
A rock is thrown upward from the top of a 112-foot high cliff overlooking the ocean at a speed of 96 feet per second. The rock’s height above ocean can be modeled by the equation [latex]H\left(t\right)=-16{t}^{2}+96t+112[/latex].
a. When does the rock reach the maximum height?
b. What is the maximum height of the rock?
c. When does the rock hit the ocean?
Show Solution
a. 3 seconds b. 256 feet c. 7 seconds