Learning Outcomes
- Define projectile motion
- Solve a polynomial function that represents projectile motion
- Interpret the solution to a polynomial function that represents projectile motion
Projectile motion happens when you throw a ball into the air and it comes back down because of gravity. A projectile will follow a curved path that behaves in a predictable way. This predictable motion has been studied for centuries, and in simple cases, an object’s height from the ground at a given time, [latex]t[/latex], can be modeled with a polynomial function of the form [latex]h(t)=at^2+bt+c[/latex], where [latex]h(t)[/latex] represents the height of an object at a given time, [latex]t[/latex]. Projectile motion is also called a parabolic trajectory because of the shape of the path of a projectile’s motion, as in the water in the image of the fountain below.

Parabolic water trajectory in a fountain.
Parabolic motion and its related functions allow us to launch satellites for telecommunications and rockets for space exploration. Recently, police departments have even begun using projectiles with GPS to track fleeing suspects in vehicles rather than pursuing them by high-speed chase [1].
In this section, we will use polynomial functions to answer questions about the parabolic motion of a projectile. The real mathematical model for the path of a rocket or a police GPS projectile may have different coefficients or more variables, but the concept remains the same. We will also learn to interpret the meaning of the variables in a polynomial function that models projectile motion.
Example
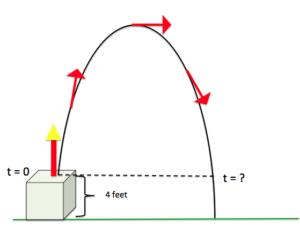
A small toy rocket is launched from a [latex]4[/latex]-foot pedestal. The height (h, in feet) of the rocket t seconds after taking off is given by the function [latex]h(t)=−2t^{2}+7t+4[/latex]. How long will it take the rocket to hit the ground?
In the next example, we will solve for the time that the rocket reaches a given height other than zero.
Example
Use the formula for the height of the rocket in the previous example to find the time when the rocket is [latex]4[/latex] feet from hitting the ground on its way back down. Refer to the image.
[latex]h(t)=−2t^{2}+7t+4[/latex]
In the following video, we show another example of how to find the time when a object following a parabolic trajectory hits the ground.
- "Cops' Latest Tool in High-speed Chases: GPS Projectiles." CBSNews. CBS Interactive, n.d. Web. [latex]14[/latex] June [latex]2016[/latex]. ↵
