Learning Outcomes
- Calculate slope for a linear function given two points
- Write the equation of a linear function given two points and a slope
Calculate and Interpret Slope
In the examples we have seen so far, we have had the slope provided for us. However, we often need to calculate the slope given input and output values. Given two values for the input, [latex]{x}_{1}[/latex] and [latex]{x}_{2}[/latex], and two corresponding values for the output, [latex]{y}_{1}[/latex] and [latex]{y}_{2}[/latex] which can be represented by a set of points, [latex]\left({x}_{1}\text{, }{y}_{1}\right)[/latex] and [latex]\left({x}_{2}\text{, }{y}_{2}\right)[/latex], we can calculate the slope [latex]m[/latex], as follows:
[latex]m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{\Delta y}{\Delta x}=\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex]
where [latex]\Delta y[/latex] is the change in output and [latex]\Delta x[/latex] is the change in input. In function notation, [latex]{y}_{1}=f\left({x}_{1}\right)[/latex] and [latex]{y}_{2}=f\left({x}_{2}\right)[/latex] so we could write:
[latex]m=\dfrac{f\left({x}_{2}\right)-f\left({x}_{1}\right)}{{x}_{2}-{x}_{1}}[/latex]
The graph below indicates how the slope of the line between the points, [latex]\left({x}_{1,}{y}_{1}\right)[/latex] and [latex]\left({x}_{2,}{y}_{2}\right)[/latex], is calculated. Recall that the slope measures steepness. The greater the absolute value of the slope, the steeper the line is.
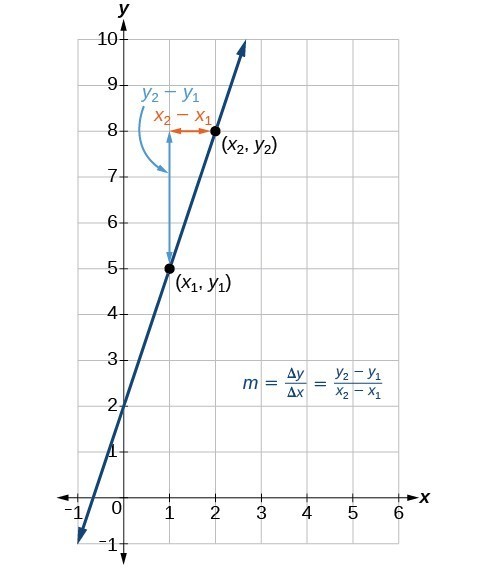
The slope of a function is calculated by the change in [latex]y[/latex] divided by the change in [latex]x[/latex]. It does not matter which coordinate is used as the [latex]\left({x}_{2,\text{ }}{y}_{2}\right)[/latex] and which is the [latex]\left({x}_{1},\text{ }{y}_{1}\right)[/latex], as long as each calculation is started with the elements from the same coordinate pair.
Q & A
Are the units for slope always [latex]\frac{\text{units for the output}}{\text{units for the input}}[/latex] ?
Yes. Think of the units as the change of output value for each unit of change in input value. An example of slope could be miles per hour or dollars per day. Notice the units appear as a ratio of units for the output per units for the input.
A General Note: CalculatING Slope
The slope, or rate of change, [latex]m[/latex], of a function can be calculated according to the following:
[latex]m=\dfrac{\text{change in output (rise)}}{\text{change in input (run)}}=\dfrac{\Delta y}{\Delta x}=\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}} \Rightarrow \dfrac{f(x_2)-f(x_1)}{x_2 - x_1}[/latex]
where [latex]{x_1}[/latex] and [latex]x_2[/latex] are input values and [latex]{f(x_1)}[/latex] and [latex]f(x_2)[/latex] are output values.
How To: Given two points from a linear function, calculate and interpret the slope.
- Determine the units for output and input values.
- Calculate the change of output values and change of input values.
- Interpret the slope as the change in output values per unit of the input value.
Example: Finding the Slope of a Linear Function
If [latex]f\left(x\right)[/latex] is a linear function and [latex]\left(3,-2\right)[/latex] and [latex]\left(8,1\right)[/latex] are points on the line, find the slope. Is this function increasing or decreasing?
Try It
If [latex]f\left(x\right)[/latex] is a linear function, and [latex]\left(2,3\right)[/latex] and [latex]\left(0,4\right)[/latex] are points on the line, find the slope. Is this function increasing or decreasing?
interpreting slope
When interpreting slope as an average rate of change, it is customary to express the calculation as change in output per unit of input.
Ex. A vehicle traveled from mile marker 57 to mile marker 180 between 4:15 pm and 6:21 pm. Can you use the formula for slope to find the vehicle’s average rate of change in distance as a function of the time it traveled?
Example: Finding the Population Change from a Linear Function
The population of a city increased from 23,400 to 27,800 between 2008 and 2012. Find the change in population per year if we assume the change was constant from 2008 to 2012.
Try It
The population of a small town increased from 1,442 to 1,868 between 2009 and 2012. Find the change in population per year if we assume the change was constant from 2009 to 2012.
recall equations of lines
The following methods of writing the equation of a line apply to writing the equation of a function. Just remember the translation: [latex]y = f(x)[/latex]. That is, graphs of functions behave exactly like lines. Wherever you see a y-coordinate, you can replace it with a function output.
Point-Slope Form
Up until now, we have been using the slope-intercept form of a linear equation to describe linear functions. Now we will learn another way to write a linear function called point-slope form which is given below:
[latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]
where [latex]m[/latex] is the slope of the linear function and [latex]({x}_{1},{y}_{1})[/latex] is any point which satisfies the linear function.
The point-slope form is derived from the slope formula.
[latex]\begin{array}{llll}{m}=\frac{y-{y}_{1}}{x-{x}_{1}}\hfill & \text{assuming }{ x }\ne {x}_{1}\hfill\\{ m }\left(x-{x}_{1}\right)=\frac{y-{y}_{1}}{x-{x}_{1}}\left(x-{x}_{1}\right)\hfill & \text{Multiply both sides by }\left(x-{x}_{1}\right)\hfill\\{ m }\left(x-{x}_{1}\right)=y-{y}_{1}\hfill & \text{Simplify}\hfill \\ y-{y}_{1}={ m }\left(x-{x}_{1}\right)\hfill &\text{Rearrange}\hfill \end{array}[/latex]
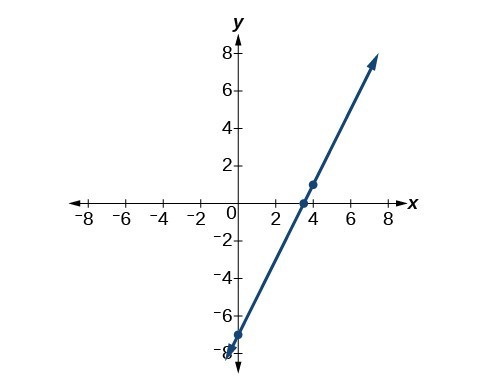
Keep in mind that slope-intercept form and point-slope form can be used to describe the same linear function. We can move from one form to another using basic algebra. For example, suppose we are given the equation [latex]y - 4=-\frac{1}{2}\left(x - 6\right)[/latex] which is in point-slope form. We can convert it to slope-intercept form as shown below.
[latex]\begin{array}{llll}y - 4=-\frac{1}{2}\left(x - 6\right)\hfill & \hfill \\ y - 4=-\frac{1}{2}x+3\hfill & \text{Distribute the }-\frac{1}{2}.\hfill \\ \text{}y=-\frac{1}{2}x+7\hfill & \text{Add 4 to each side}.\hfill \end{array}[/latex]
Therefore, the same line can be described in slope-intercept form as [latex]y=-\frac{1}{2}x+7[/latex].
A General Note: Point-Slope Form of a Linear Equation
Point-slope form of a linear equation takes the form
[latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]
where [latex]m[/latex] is the slope and [latex]{x}_{1 }\text{ and } {y}_{1}[/latex] are the [latex]x\text{ and }y[/latex] coordinates of a specific point through which the line passes.
Point-slope form is particularly useful if we know one point and the slope of a line. For example, suppose we are told that a line has a slope of 2 and passes through the point [latex]\left(4,1\right)[/latex]. We know that [latex]m=2[/latex] and that [latex]{x}_{1}=4[/latex] and [latex]{y}_{1}=1[/latex]. We can substitute these values into point-slope form.
[latex]\begin{array}{l}y-{y}_{1}=m\left(x-{x}_{1}\right)\\ y - 1=2\left(x - 4\right)\end{array}[/latex]
If we wanted to rewrite the equation in slope-intercept form, we apply algebraic techniques.
[latex]\begin{array}{llll} y - 1=2\left(x - 4\right)\hfill & \hfill \\ y - 1=2x - 8\hfill & \text{Distribute the }2.\hfill \\ \text{}y=2x - 7\hfill & \text{Add 1 to each side}.\hfill \end{array}[/latex]
Both equations [latex]y - 1=2\left(x - 4\right)[/latex] and [latex]y=2x - 7[/latex] describe the same line. The graph of the line can be seen below.
Example: Writing Linear Equations Using a Point and the Slope
Write the point-slope form of an equation of a line with a slope of 3 that passes through the point [latex]\left(6,-1\right)[/latex]. Then rewrite the equation in slope-intercept form.
Try It
Write the equation of a line in point-slope form with a slope of [latex]-2[/latex] that passes through the point [latex]\left(-2,\text{ }2\right)[/latex]. Then rewrite the equation in the slope-intercept form.
Writing the Equation of a Line Using Two Points
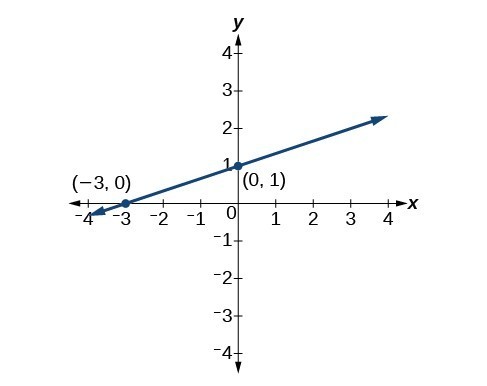
Point-slope form of an equation is also useful if we know any two points through which a line passes. Suppose, for example, we know that a line passes through the points [latex]\left(0,\text{ }1\right)[/latex] and [latex]\left(3,\text{ }2\right)[/latex]. We can use the coordinates of the two points to find the slope.
[latex]\begin{array}{l}{m}=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\\ \text{}{m}=\frac{2 - 1}{3 - 0}\hfill \\ \text{}{m}=\frac{1}{3}\hfill \end{array}[/latex]
Now we can use the slope we found and the coordinates of one of the points to find the equation for the line. Let’s use (0, 1) for our point.
[latex]\begin{array}{l}y-{y}_{1}=m\left(x-{x}_{1}\right)\\ y - 1=\frac{1}{3}\left(x - 0\right)\end{array}[/latex]
As before, we can use algebra to rewrite the equation in slope-intercept form.
[latex]\begin{array}{lll}y - 1=\frac{1}{3}\left(x - 0\right)\hfill & \hfill \\ y - 1=\frac{1}{3}x\hfill & \text{Distribute the }\frac{1}{3}.\hfill \\ \text{}y=\frac{1}{3}x+1\hfill & \text{Add 1 to each side}.\hfill \end{array}[/latex]
Both equations describe the line graphed below.
Example: Writing Linear Equations Using Two Points
Write the point-slope form of an equation of a line that passes through the points [latex]\left(5,\text{ }1\right)[/latex] and [latex]\left(8,\text{ }7\right)[/latex]. Then rewrite the equation in slope-intercept form.
Try It
Write the point-slope form of an equation of a line that passes through the points [latex]\left(-1,3\right)[/latex] and [latex]\left(0,0\right)[/latex]. Then rewrite the equation in slope-intercept form.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Question ID 113460, 76345. Authored by: Lumen Learning. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/9b08c294-057f-4201-9f48-5d6ad992740d@5.2
- Question ID 2100, 2102. Authored by: Morales,Lawrence. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
