Learning Outcomes
- Determine the number of objects being represented by pebbles placed on an Inca counting board.
- Determine the number represented by a quipu cord
- Identify uses other than counting for a quipu cord
The Need for Simple Counting
As societies and humankind evolved, simply having a sense of more or less, even or odd, etc., would prove to be insufficient to meet the needs of everyday living. As tribes and groups formed, it became important to be able to know how many members were in the group, and perhaps how many were in the enemy’s camp. Certainly it was important for them to know if the flock of sheep or other possessed animals were increasing or decreasing in size. “Just how many of them do we have, anyway?” is a question that we do not have a hard time imagining them asking themselves (or each other).
In order to count items such as animals, it is often conjectured that one of the earliest methods of doing so would be with “tally sticks.” These are objects used to track the numbers of items to be counted. With this method, each “stick” (or pebble, or whatever counting device being used) represents one animal or object. This method uses the idea of one to one correspondence. In a one to one correspondence, items that are being counted are uniquely linked with some counting tool.
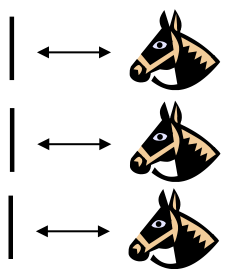
Figure 1.
In the picture to the right, you see each stick corresponding to one horse. By examining the collection of sticks in hand one knows how many animals should be present. You can imagine the usefulness of such a system, at least for smaller numbers of items to keep track of. If a herder wanted to “count off” his animals to make sure they were all present, he could mentally (or methodically) assign each stick to one animal and continue to do so until he was satisfied that all were accounted for.
Of course, in our modern system, we have replaced the sticks with more abstract objects. In particular, the top stick is replaced with our symbol “1,” the second stick gets replaced by a “2” and the third stick is represented by the symbol “3,” but we are getting ahead of ourselves here. These modern symbols took many centuries to emerge.
Another possible way of employing the “tally stick” counting method is by making marks or cutting notches into pieces of wood, or even tying knots in string (as we shall see later). In 1937, Karl Absolom discovered a wolf bone that goes back possibly 30,000 years. It is believed to be a counting device.[1] Another example of this kind of tool is the Ishango Bone, discovered in 1960 at Ishango, and shown below.[2] It is reported to be between six and nine thousand years old and shows what appear to be markings used to do counting of some sort.
The markings on rows (a) and (b) each add up to 60. Row (b) contains the prime numbers between 10 and 20. Row (c) seems to illustrate for the method of doubling and multiplication used by the Egyptians. It is believed that this may also represent a lunar phase counter.

Figure 2.
Spoken Words
As methods for counting developed, and as language progressed as well, it is natural to expect that spoken words for numbers would appear. Unfortunately, the developments of these words, especially those corresponding to the numbers from one through ten, are not easy to trace. Past ten, however, we do see some patterns:
- Eleven comes from “ein lifon,” meaning “one left over.”
- Twelve comes from “twe lif,” meaning “two left over.”
- Thirteen comes from “Three and ten” as do fourteen through nineteen.
- Twenty appears to come from “twe-tig” which means “two tens.”
- Hundred probably comes from a term meaning “ten times.”
Written Numbers
When we speak of “written” numbers, we have to be careful because this could mean a variety of things. It is important to keep in mind that modern paper is only a little more than 100 years old, so “writing” in times past often took on forms that might look quite unfamiliar to us today.
As we saw earlier, some might consider wooden sticks with notches carved in them as writing as these are means of recording information on a medium that can be “read” by others. Of course, the symbols used (simple notches) certainly did not leave a lot of flexibility for communicating a wide variety of ideas or information.
Other mediums on which “writing” may have taken place include carvings in stone or clay tablets, rag paper made by hand (twelfth century in Europe, but earlier in China), papyrus (invented by the Egyptians and used up until the Greeks), and parchments from animal skins. And these are just a few of the many possibilities.
These are just a few examples of early methods of counting and simple symbols for representing numbers. Extensive books, articles and research have been done on this topic and could provide enough information to fill this entire course if we allowed it to. The range and diversity of creative thought that has been used in the past to describe numbers and to count objects and people is staggering. Unfortunately, we don’t have time to examine them all, but it is fun and interesting to look at one system in more detail to see just how ingenious people have been.
The Number and Counting System of the Inca Civilization
Background
There is generally a lack of books and research material concerning the historical foundations of the Americas. Most of the “important” information available concentrates on the eastern hemisphere, with Europe as the central focus. The reasons for this may be twofold: first, it is thought that there was a lack of specialized mathematics in the American regions; second, many of the secrets of ancient mathematics in the Americas have been closely guarded.[3] The Peruvian system does not seem to be an exception here. Two researchers, Leland Locke and Erland Nordenskiold, have carried out research that has attempted to discover what mathematical knowledge was known by the Incas and how they used the Peruvian quipu, a counting system using cords and knots, in their mathematics. These researchers have come to certain beliefs about the quipu that we will summarize here.
Counting Boards
It should be noted that the Incas did not have a complicated system of computation. Where other peoples in the regions, such as the Mayans, were doing computations related to their rituals and calendars, the Incas seem to have been more concerned with the simpler task of record-keeping. To do this, they used what are called the “quipu” to record quantities of items. (We will describe them in more detail in a moment.) However, they first often needed to do computations whose results would be recorded on quipu. To do these computations, they would sometimes use a counting board constructed with a slab of stone. In the slab were cut rectangular and square compartments so that an octagonal (eight-sided) region was left in the middle. Two opposite corner rectangles were raised. Another two sections were mounted on the original surface of the slab so that there were actually three levels available. In the figure shown, the darkest shaded corner regions represent the highest, third level. The lighter shaded regions surrounding the corners are the second highest levels, while the clear white rectangles are the compartments cut into the stone slab.
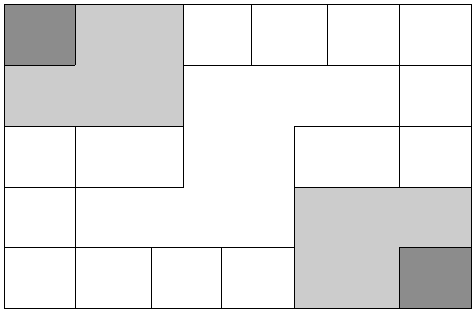
Figure 3.
Pebbles were used to keep accounts and their positions within the various levels and compartments gave totals. For example, a pebble in a smaller (white) compartment represented one unit. Note that there are 12 such squares around the outer edge of the figure. If a pebble was put into one of the two (white) larger, rectangular compartments, its value was doubled. When a pebble was put in the octagonal region in the middle of the slab, its value was tripled. If a pebble was placed on the second (shaded) level, its value was multiplied by six. And finally, if a pebble was found on one of the two highest corner levels, its value was multiplied by twelve. Different objects could be counted at the same time by representing different objects by different colored pebbles.
Example
Suppose you have the following counting board with two different kind of pebbles places as illustrated. Let the solid black pebble represent a dog and the striped pebble represent a cat. How many dogs are being represented?
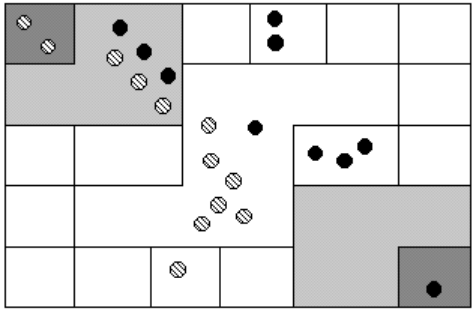
Try It
How many cats are represented on this board?

Watch this short video lesson about Inca counting boards. You will find that this is a review of concepts presented here about counting boards.
The Quipu
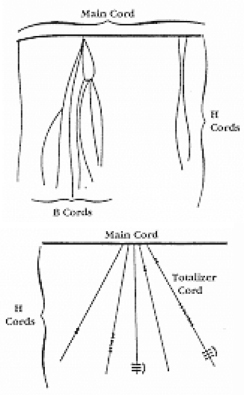
Figure 5.
This kind of board was good for doing quick computations, but it did not provide a good way to keep a permanent recording of quantities or computations. For this purpose, they used the quipu. The quipu is a collection of cords with knots in them. These cords and knots are carefully arranged so that the position and type of cord or knot gives specific information on how to decipher the cord.
A quipu is made up of a main cord which has other cords (branches) tied to it. See pictures to the right.[4]
Locke called the branches H cords. They are attached to the main cord. B cords, in turn, were attached to the H cords. Most of these cords would have knots on them. Rarely are knots found on the main cord, however, and tend to be mainly on the H and B cords. A quipu might also have a “totalizer” cord that summarizes all of the information on the cord group in one place.
Locke points out that there are three types of knots, each representing a different value, depending on the kind of knot used and its position on the cord. The Incas, like us, had a decimal (base-ten) system, so each kind of knot had a specific decimal value. The Single knot, pictured in the middle of figure 6[5] was used to denote tens, hundreds, thousands, and ten thousands. They would be on the upper levels of the H cords. The figure-eight knot on the end was used to denote the integer “one.” Every other integer from 2 to 9 was represented with a long knot, shown on the left of the figure. (Sometimes long knots were used to represents tens and hundreds.) Note that the long knot has several turns in it…the number of turns indicates which integer is being represented. The units (ones) were placed closest to the bottom of the cord, then tens right above them, then the hundreds, and so on.
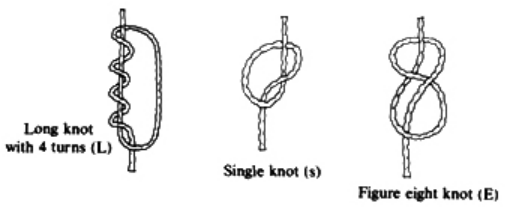
Figure 6
In order to make reading these pictures easier, we will adopt a convention that is consistent. For the long knot with turns in it (representing the numbers 2 through 9), we will use the following notation:
The four horizontal bars represent four turns and the curved arc on the right links the four turns together. This would represent the number 4.
We will represent the single knot with a large dot ( · ) and we will represent the figure eight knot with a sideways eight ( ∞ ).
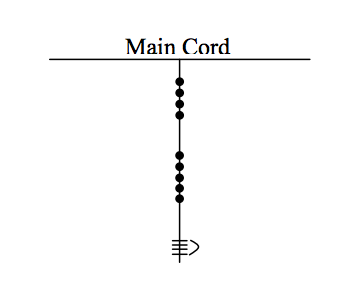
Example
What number is represented on the cord shown in figure 7?
Try It
What numbers are represented on each of the four cords hanging from the main cord?
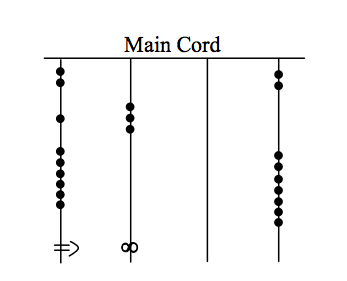
The colors of the cords had meaning and could distinguish one object from another. One color could represent llamas, while a different color might represent sheep, for example. When all the colors available were exhausted, they would have to be re-used. Because of this, the ability to read the quipu became a complicated task and specially trained individuals did this job. They were called Quipucamayoc, which means keeper of the quipus. They would build, guard, and decipher quipus.
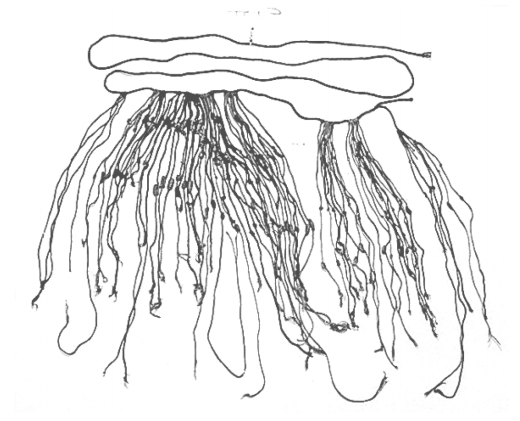
Figure 9.
As you can see from this photograph of an actual quipu (figure 9), they could get quite complex.
There were various purposes for the quipu. Some believe that they were used to keep an account of their traditions and history, using knots to record history rather than some other formal system of writing. One writer has even suggested that the quipu replaced writing as it formed a role in the Incan postal system.[6] Another proposed use of the quipu is as a translation tool. After the conquest of the Incas by the Spaniards and subsequent “conversion” to Catholicism, an Inca supposedly could use the quipu to confess their sins to a priest. Yet another proposed use of the quipu was to record numbers related to magic and astronomy, although this is not a widely accepted interpretation.
The following video presents another introduction to the Inca’s use of a quipu for record keeping.
The mysteries of the quipu have not been fully explored yet. Recently, Ascher and Ascher have published a book, The Code of the Quipu: A Study in Media, Mathematics, and Culture, which is “an extensive elaboration of the logical-numerical system of the quipu.”[7] For more information on the quipu, you may want to check out “Khipus: a unique Huarochiri legacy.”
We are so used to seeing the symbols 1, 2, 3, 4, etc. that it may be somewhat surprising to see such a creative and innovative way to compute and record numbers. Unfortunately, as we proceed through our mathematical education in grade and high school, we receive very little information about the wide range of number systems that have existed and which still exist all over the world. That’s not to say our own system is not important or efficient. The fact that it has survived for hundreds of years and shows no sign of going away any time soon suggests that we may have finally found a system that works well and may not need further improvement, but only time will tell that whether or not that conjecture is valid or not. We now turn to a brief historical look at how our current system developed over history.
- Bunt, Lucas; Jones, Phillip; Bedient, Jack; The Historical Roots of Elementary Mathematics, p. 2. ↵
- http://www.math.buffalo.edu/mad/Ancient-Africa/mad_zaire-uganda.html ↵
- Diana, Lind Mae; The Peruvian Quipu in Mathematics Teacher, Issue 60 (Oct., 1967), p. 623–28. ↵
- Diana, Lind Mae; The Peruvian Quipu in Mathematics Teacher, Issue 60 (Oct., 1967), p. 623–28. ↵
- http://wiscinfo.doit.wisc.edu/chaysimire/titulo2/khipus/what.htm ↵
- Diana, Lind Mae; The Peruvian Quipu in Mathematics Teacher, Issue 60 (Oct., 1967), p. 623–28. ↵
- http://www.cs.uidaho.edu/~casey931/seminar/quipu.html ↵
