Learning Objectives
- Become familiar with the evolution of the counting system we use every day
- Write numbers using Roman Numerals
- Convert between Hindu-Arabic and Roman Numerals
The Evolution of a System
Our own number system, composed of the ten symbols {0,1,2,3,4,5,6,7,8,9} is called the Hindu-Arabic system. This is a base-ten (decimal) system since place values increase by powers of ten. Furthermore, this system is positional, which means that the position of a symbol has bearing on the value of that symbol within the number. For example, the position of the symbol 3 in the number 435,681 gives it a value much greater than the value of the symbol 8 in that same number. We’ll explore base systems more thoroughly later. The development of these ten symbols and their use in a positional system comes to us primarily from India.[1]

Figure 10. Al-Biruni
It was not until the fifteenth century that the symbols that we are familiar with today first took form in Europe. However, the history of these numbers and their development goes back hundreds of years. One important source of information on this topic is the writer al-Biruni, whose picture is shown in figure 10.[2] Al-Biruni, who was born in modern day Uzbekistan, had visited India on several occasions and made comments on the Indian number system. When we look at the origins of the numbers that al-Biruni encountered, we have to go back to the third century BCE to explore their origins. It is then that the Brahmi numerals were being used.
The Brahmi numerals were more complicated than those used in our own modern system. They had separate symbols for the numbers 1 through 9, as well as distinct symbols for 10, 100, 1000,…, also for 20, 30, 40,…, and others for 200, 300, 400, …, 900. The Brahmi symbols for 1, 2, and 3 are shown below.[3]
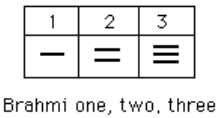
These numerals were used all the way up to the fourth century CE, with variations through time and geographic location. For example, in the first century CE, one particular set of Brahmi numerals took on the following form:[4]
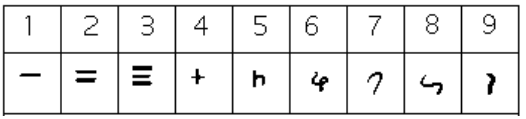
From the fourth century on, you can actually trace several different paths that the Brahmi numerals took to get to different points and incarnations. One of those paths led to our current numeral system, and went through what are called the Gupta numerals. The Gupta numerals were prominent during a time ruled by the Gupta dynasty and were spread throughout that empire as they conquered lands during the fourth through sixth centuries. They have the following form:[5]
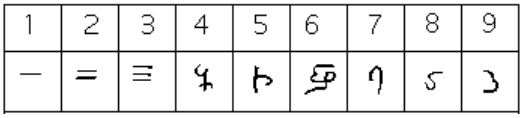
How the numbers got to their Gupta form is open to considerable debate. Many possible hypotheses have been offered, most of which boil down to two basic types.[6] The first type of hypothesis states that the numerals came from the initial letters of the names of the numbers. This is not uncommon . . . the Greek numerals developed in this manner. The second type of hypothesis states that they were derived from some earlier number system. However, there are other hypotheses that are offered, one of which is by the researcher Ifrah. His theory is that there were originally nine numerals, each represented by a corresponding number of vertical lines. One possibility is this:[7]
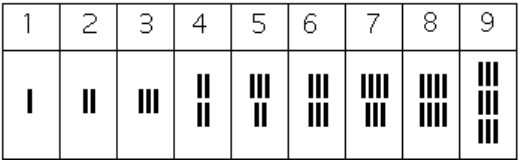
Because these symbols would have taken a lot of time to write, they eventually evolved into cursive symbols that could be written more quickly. If we compare these to the Gupta numerals above, we can try to see how that evolutionary process might have taken place, but our imagination would be just about all we would have to depend upon since we do not know exactly how the process unfolded.
The Gupta numerals eventually evolved into another form of numerals called the Nagari numerals, and these continued to evolve until the eleventh century, at which time they looked like this:[8]
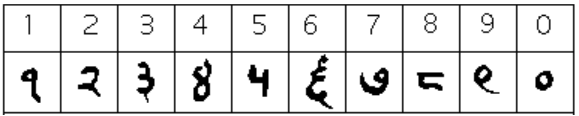
Note that by this time, the symbol for 0 has appeared! The Mayans in the Americas had a symbol for zero long before this, however, as we shall see later in the chapter.
These numerals were adopted by the Arabs, most likely in the eighth century during Islamic incursions into the northern part of India.[9] It is believed that the Arabs were instrumental in spreading them to other parts of the world, including Spain (see below).
Other examples of variations up to the eleventh century include:[10]

Figure 11. Devangari, eighth century

Figure 12. West Arab Gobar, tenth century
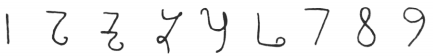
Figure 13. Spain, 976 BCE
Finally, figure 14[11] shows various forms of these numerals as they developed and eventually converged to the fifteenth century in Europe.
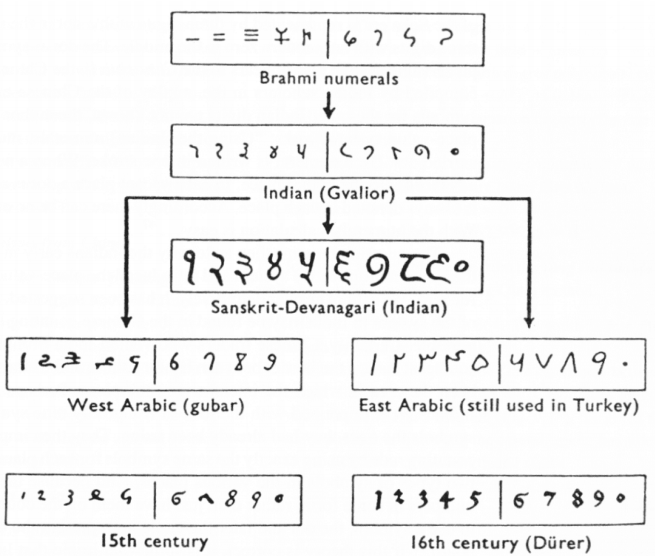
Figure 14.
Roman Numerals
The numeric system represented by Roman numerals originated in ancient Rome (753 BC–476 AD) and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages (generally comprising the 14th and 15th centuries (c. 1301–1500)). Numbers in this system are represented by combinations of letters from the Latin alphabet. Roman numerals, as used today, are based on seven symbols:
| Symbol | I | V | X | L | C | D | M |
| Value | 1 | 5 | 10 | 50 | 100 | 500 | 1,000 |
The use of Roman numerals continued long after the decline of the Roman Empire. From the 14th century on, Roman numerals began to be replaced in most contexts by the more convenient Hindu-Arabic numerals; however, this process was gradual, and the use of Roman numerals persists in some minor applications to this day.
The numbers 1 to 10 are usually expressed in Roman numerals as follows:
- I, II, III, IV, V, VI, VII, VIII, IX, X.
Numbers are formed by combining symbols and adding the values, so II is two (two ones) and XIII is thirteen (a ten and three ones). Because each numeral has a fixed value rather than representing multiples of ten, one hundred and so on, according to position, there is no need for “place keeping” zeros, as in numbers like 207 or 1066; those numbers are written as CCVII (two hundreds, a five and two ones) and MLXVI (a thousand, a fifty, a ten, a five and a one).
Symbols are placed from left to right in order of value, starting with the largest. However, in a few specific cases, to avoid four characters being repeated in succession (such as IIII or XXXX), subtractive notation is used: as in this table:
| Number | 4 | 9 | 40 | 90 | 400 | 900 |
| Roman Numeral | IV | IX | XL | XC | CD | CM |
In summary:
- I placed before V or X indicates one less, so four is IV (one less than five) and nine is IX (one less than ten)
- X placed before L or C indicates ten less, so forty is XL (ten less than fifty) and ninety is XC (ten less than a hundred)
- C placed before D or M indicates a hundred less, so four hundred is CD (a hundred less than five hundred) and nine hundred is CM (a hundred less than a thousand)
Example
Write the Hindu-Arabic numeral for MCMIV.
Try It
Modern use
By the 11th century, Hindu–Arabic numerals had been introduced into Europe from al-Andalus, by way of Arab traders and arithmetic treatises. Roman numerals, however, proved very persistent, remaining in common use in the West well into the 14th and 15th centuries, even in accounting and other business records (where the actual calculations would have been made using an abacus). Replacement by their more convenient “Arabic” equivalents was quite gradual, and Roman numerals are still used today in certain contexts. A few examples of their current use are:
- Names of monarchs and popes, e.g. Elizabeth II of the United Kingdom, Pope Benedict XVI. These are referred to as regnal numbers; e.g. II is pronounced “the second”. This tradition began in Europe sporadically in the Middle Ages, gaining widespread use in England only during the reign of Henry VIII. Previously, the monarch was not known by numeral but by an epithet such as Edward the Confessor. Some monarchs (e.g. Charles IV of Spain and Louis XIV of France) seem to have preferred the use of IIII instead of IV on their coinage (see illustration).
- Generational suffixes, particularly in the US, for people sharing the same name across generations, for example William Howard Taft IV.
- In the French Republican Calendar, initiated during the French Revolution, years were numbered by Roman numerals – from the year I (1792) when this calendar was introduced to the year XIV (1805) when it was abandoned.
- The year of production of films, television shows and other works of art within the work itself. It has been suggested – by BBC News, perhaps facetiously – that this was originally done “in an attempt to disguise the age of films or television programmes.”[23] Outside reference to the work will use regular Hindu–Arabic numerals.
- Hour marks on timepieces. In this context, 4 is usually written IIII.
- The year of construction on building faces and cornerstones.
- Page numbering of prefaces and introductions of books, and sometimes of annexes, too.
- Book volume and chapter numbers, as well as the several acts within a play (e.g. Act iii, Scene 2).
- Sequels of some movies, video games, and other works (as in Rocky II).
- Outlines that use numbers to show hierarchical relationships.
- Occurrences of a recurring grand event, for instance:
- The Summer and Winter Olympic Games (e.g. the XXI Olympic Winter Games; the Games of the XXX Olympiad)
- The Super Bowl, the annual championship game of the National Football League (e.g. Super Bowl XXXVII; Super Bowl 50 is a one-time exception[24])
- WrestleMania, the annual professional wrestling event for the WWE (e.g. WrestleMania XXX). This usage has also been inconsistent.
- http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html ↵
- http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/Al-Biruni.html ↵
- http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html ↵
- http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Indian_numerals.html ↵
- Ibid. ↵
- Ibid. ↵
- Ibid. ↵
- Ibid. ↵
- Katz, page 230 ↵
- Burton, David M., History of Mathematics, An Introduction, p. 254–255 ↵
- Katz, page 231. ↵

