Learning Outcomes
- Determine whether data or a scenario describe linear or geometric growth
- Identify growth rates, initial values, or point values expressed verbally, graphically, or numerically, and translate them into a format usable in calculation
- Calculate recursive and explicit equations for linear and geometric growth given sufficient information, and use those equations to make predictions
Predicting Growth
Marco is a collector of antique soda bottles. His collection currently contains 437 bottles. Every year, he budgets enough money to buy 32 new bottles. Can we determine how many bottles he will have in 5 years, and how long it will take for his collection to reach 1000 bottles?
While you could probably solve both of these questions without an equation or formal mathematics, we are going to formalize our approach to this problem to provide a means to answer more complicated questions.
Suppose that Pn represents the number, or population, of bottles Marco has after n years. So P0 would represent the number of bottles now, P1 would represent the number of bottles after 1 year, P2 would represent the number of bottles after 2 years, and so on. We could describe how Marco’s bottle collection is changing using:
P0 = 437
Pn = Pn-1 + 32
This is called a recursive relationship. A recursive relationship is a formula which relates the next value in a sequence to the previous values. Here, the number of bottles in year n can be found by adding 32 to the number of bottles in the previous year, Pn-1. Using this relationship, we could calculate:
P1 = P0 + 32 = 437 + 32 = 469
P2 = P1 + 32 = 469 + 32 = 501
P3 = P2 + 32 = 501 + 32 = 533
P4 = P3 + 32 = 533 + 32 = 565
P5 = P4 + 32 = 565 + 32 = 597
We have answered the question of how many bottles Marco will have in 5 years. 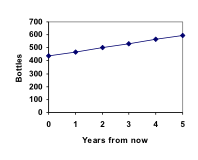
However, solving how long it will take for his collection to reach 1000 bottles would require a lot more calculations.
While recursive relationships are excellent for describing simply and cleanly how a quantity is changing, they are not convenient for making predictions or solving problems that stretch far into the future. For that, a closed or explicit form for the relationship is preferred. An explicit equation allows us to calculate Pn directly, without needing to know Pn-1. While you may already be able to guess the explicit equation, let us derive it from the recursive formula. We can do so by selectively not simplifying as we go:
P1 = 437 + 32 = 437 + 1(32)
P2 = P1 + 32 = 437 + 32 + 32 = 437 + 2(32)
P3 = P2 + 32 = (437 + 2(32)) + 32 = 437 + 3(32)
P4 = P3 + 32 = (437 + 3(32)) + 32 = 437 + 4(32)
You can probably see the pattern now, and generalize that
Pn = 437 + n(32) = 437 + 32n
Using this equation, we can calculate how many bottles he’ll have after 5 years:
P5 = 437 + 32(5) = 437 + 160 = 597
We can now also solve for when the collection will reach 1000 bottles by substituting in 1000 for Pn and solving for n
1000 = 437 + 32n
563 = 32n
n = 563/32 = 17.59
So Marco will reach 1000 bottles in 18 years.
The steps of determining the formula and solving the problem of Marco’s bottle collection are explained in detail in the following videos.
In this example, Marco’s collection grew by the same number of bottles every year. This constant change is the defining characteristic of linear growth. Plotting the values we calculated for Marco’s collection, we can see the values form a straight line, the shape of linear growth.
Linear Growth
If a quantity starts at size P0 and grows by d every time period, then the quantity after n time periods can be determined using either of these relations:
Recursive form
Pn = Pn-1 + d
Explicit form
Pn = P0 + d n
In this equation, d represents the common difference – the amount that the population changes each time n increases by 1.
Connection to Prior Learning: Slope and Intercept
You may recognize the common difference, d, in our linear equation as slope. In fact, the entire explicit equation should look familiar – it is the same linear equation you learned in algebra, probably stated as y = mx + b.
In the standard algebraic equation y = mx + b, b was the y-intercept, or the y value when x was zero. In the form of the equation we’re using, we are using P0 to represent that initial amount.
In the y = mx + b equation, recall that m was the slope. You might remember this as “rise over run,” or the change in y divided by the change in x. Either way, it represents the same thing as the common difference, d, we are using – the amount the output Pn changes when the input n increases by 1.
The equations y = mx + b and Pn = P0 + d n mean the same thing and can be used the same ways. We’re just writing it somewhat differently.
Examples
The population of elk in a national forest was measured to be 12,000 in 2003, and was measured again to be 15,000 in 2007. If the population continues to grow linearly at this rate, what will the elk population be in 2014?
View more about this example here.
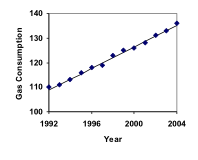
Gasoline consumption in the US has been increasing steadily. Consumption data from 1992 to 2004 is shown below.[1] Find a model for this data, and use it to predict consumption in 2016. If the trend continues, when will consumption reach 200 billion gallons?
| Year | ’92 | ’93 | ’94 | ’95 | ’96 | ’97 | ’98 | ’99 | ’00 | ’01 | ’02 | ’03 | ’04 |
| Consumption (billion of gallons) | 110 | 111 | 113 | 116 | 118 | 119 | 123 | 125 | 126 | 128 | 131 | 133 | 136 |
The steps for reaching this answer are detailed in the following video.
The cost, in dollars, of a gym membership for n months can be described by the explicit equation Pn = 70 + 30n. What does this equation tell us?
The explanation for this example is detailed below.
Try It
The number of stay-at-home fathers in Canada has been growing steadily[2]. While the trend is not perfectly linear, it is fairly linear. Use the data from 1976 and 2010 to find an explicit formula for the number of stay-at-home fathers, then use it to predict the number in 2020.
| Year | 1976 | 1984 | 1991 | 2000 | 2010 |
| # of Stay -at-home fathers | 20610 | 28725 | 43530 | 47665 | 53555 |
When Good Models Go Bad
When using mathematical models to predict future behavior, it is important to keep in mind that very few trends will continue indefinitely.
Example
Suppose a four year old boy is currently 39 inches tall, and you are told to expect him to grow 2.5 inches a year.
We can set up a growth model, with n = 0 corresponding to 4 years old.
Recursive form
P0 = 39
Pn = Pn-1 + 2.5
Explicit form
Pn = 39 + 2.5n
So at 6 years old, we would expect him to be
P2 = 39 + 2.5(2) = 44 inches tall
Any mathematical model will break down eventually. Certainly, we shouldn’t expect this boy to continue to grow at the same rate all his life. If he did, at age 50 he would be
P46 = 39 + 2.5(46) = 154 inches tall = 12.8 feet tall!
When using any mathematical model, we have to consider which inputs are reasonable to use. Whenever we extrapolate, or make predictions into the future, we are assuming the model will continue to be valid.
View a video explanation of this breakdown of the linear growth model here.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Linear (Algebraic) Growth. Authored by: David Lippman. Located at: http://www.opentextbookstore.com/mathinsociety/. Project: Math in Society. License: CC BY-SA: Attribution-ShareAlike
- Feira Tom Jobim - BH. Authored by: Antonio Thomas Koenigkam Oliveira. Located at: https://flic.kr/p/p8ZqqF. License: CC BY: Attribution
- Linear Growth Part 1. Authored by: OCLPhase2's channel. Located at: https://youtu.be/SJcAjN-HL_I. License: CC BY: Attribution
- Linear Growth Part 2. Authored by: OCLPhase2's channel. Located at: https://youtu.be/4Two_oduhrA. License: CC BY: Attribution
- Linear Growth Part 3. Authored by: OCLPhase2's channel. Located at: https://youtu.be/pZ4u3j8Vmzo. License: CC BY: Attribution
- Linear Growth - Elk. Authored by: OCLPhase2's channel. Located at: https://youtu.be/J1XqqlKzYGs. License: CC BY: Attribution
- Finding linear model for gas consumption. Authored by: OCLPhase2's channel. Located at: https://youtu.be/ApFxDWd6IbE. License: CC BY: Attribution
- Interpreting a linear model. Authored by: OCLPhase2's channel. Located at: https://youtu.be/0Uwz5dmLTtk. License: CC BY: Attribution
- Linear model breakdown. Authored by: OCLPhase2's channel. Located at: https://youtu.be/6zfXCsmcDzI. License: CC BY: Attribution
- Question ID 6594. Authored by: Lippman,David. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL