Solving Multi-Step Equations

Learning outcome

Solve multi-step equations with variables on both sides

In the examples up to this point, we have been able to isolate the variable with just one operation. Many of the equations we encounter in real life will take more steps to solve. Often, we will need to simplify one or both sides of an equation before using the Subtraction or Addition Properties of Equality. You should always simplify as much as possible before trying to isolate the variable — this is called combining like-terms.

Example

Solve:

[latex]3x - 7 - 2x - 4=1[/latex]

Solution:
The left side of the equation has an expression that we should simplify before trying to isolate the variable.

	[latex]3x-7-2x-4=1[/latex]
Rearrange the terms, using the Commutative Property of Addition.	[latex]3x-2x-7-4=1[/latex]
Combine like terms.	[latex]x-11=1[/latex]
Add [latex]11[/latex] to both sides to isolate [latex]x[/latex] .	[latex]x-11\color{red}{+11}=1\color{red}{+11}[/latex]
Simplify.	[latex]x=12[/latex]
Check. Substitute [latex]x=12[/latex] into the original equation. [latex]3x-7-2x-4=1[/latex] [latex]3(\color{red}{12})-7-2(\color{red}{12})-4=1[/latex] [latex]36-7-24-4=1[/latex] [latex]29-24-4=1[/latex] [latex]5-4=1[/latex] [latex]1=1\quad\checkmark[/latex] The solution checks.

Now you can try solving a couple equations where you should simplify first.

TRY IT

The goal has been to familiarize you with the many ways to apply the addition, subtraction, multiplication, and division properties that are used to solve equations algebraically. Let’s work through an example that will employ all the techniques you’ve learned.

Example

Solve: [latex]8x+9x - 5x=-3+15[/latex]

Solution:

First, we need to simplify both sides of the equation as much as possible

Start by combining like terms to simplify each side.

	[latex]8x+9x-5x=-3+15[/latex]
Combine like terms.	[latex]12x=12[/latex]
Divide both sides by 12 to isolate x.	[latex]\Large\frac{12x}{\color{red}{12}}\normalsize =\Large\frac{12}{\color{red}{12}}[/latex]
Simplify.	[latex]x=1[/latex]
Check your answer. Let [latex]x=1[/latex]
[latex]8x+9x-5x=-3+15[/latex]
[latex]8\cdot\color{red}{1}+9\cdot\color{red}{1}-5\cdot\color{red}{1}\stackrel{\text{?}}{=}-3+15[/latex]
[latex]8+9-5\stackrel{\text{?}}{=}-3+15[/latex]
[latex]12=12\quad\checkmark[/latex]

Here is a similar problem for you to try.

Try it

In the following video we present another example of how to solve an equation that requires simplifying before using the addition and subtraction properties.

You may not always have the variables on the left side of the equation, so we will show an example with variables on the right side. You will see that the properties used to solve this equation are exactly the same as the previous example.

example

Solve: [latex]11 - 20=17y - 8y - 6y[/latex]

Show Answer

Notice that the variable ended up on the right side of the equal sign when we solved the equation. You may prefer to take one more step to write the solution with the variable on the left side of the equal sign.

Now you can try solving a similar problem.

try it

In our next example, we have an equation that contains a set of parentheses. We will use the distributive property of multiplication over addition first, simplify, then use the division property to finally solve.

Let’s review how the Distributive Property works.

Distributive Property

If [latex]a,b,c[/latex] are real numbers, then

[latex]a\left(b+c\right)=ab+ac[/latex]

example

Simplify: [latex]3\left(x+4\right)[/latex]

Solution:

[latex]3\left(x+4\right)[/latex]
Distribute.	[latex]3\cdot x+3\cdot 4[/latex]
Multiply.	[latex]3x+12[/latex]

Some students find it helpful to draw in arrows to remind them how to use the Distributive Property. Then the first step in the previous example would look like this:

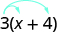
The image shows the expression x plus 4 in parentheses with the number 3 outside the parentheses on the left. There are two arrows pointing from the top of the three. One arrow points to the top of the x. The other arrow points to the top of the 4.

[latex]3\cdot x+3\cdot 4[/latex]

Now you give it a try.

try it

Apply your understanding of the Distributive Property to an equation that needs to be solved.

example

Solve: [latex]-3\left(n - 2\right)-6=21[/latex]

Remember—always simplify each side first.

Show Answer

Now you can try a similar problem.

try it

In the following video you will see another example of using the division property of equality to solve an equation as well as another example of how to solve a multi-step equation that includes a set of parentheses.

You may have noticed that in all the equations we have solved so far, we had variables on only one side of the equation. This does not happen all the time—so now we’ll see how to solve equations where there are variable terms on both sides of the equation. We will start like we did above—choosing a variable side and a constant side, and then use the Subtraction and Addition Properties of Equality to collect all variables on one side and all constants on the other side. Remember, what you do to the left side of the equation, you must do to the right side as well.

In the next example, the variable, [latex]x[/latex], is on both sides, but the constants appear only on the right side, so we’ll make the right side the “constant” side. Then the left side will be the “variable” side.

ExampleS

Solve: [latex]5x=4x+7[/latex]

Show Answer

Solve: [latex]7x=-x+24[/latex].

Show Answer

Now you can try solving an equation with variables on both sides where it is beneficial to move the variable term to the left side.

try it

In our last examples, we moved the variable term to the left side of the equation. In the next example, you will see that it is beneficial to move the variable term to the right side of the equation. There is no “correct” side to move the variable term, but the choice can help you avoid working with negative signs.

example

Solve: [latex]5y - 8=7y[/latex]

Show Answer

Now you can try solving an equation where it is beneficial to move the variable term to the right side.

try it

Solve Equations with Variables and Constants on Both Sides

The next example will be the first to have variables and constants on both sides of the equation. As we did before, we’ll collect the variable terms to one side and the constants to the other side. You will see that as the number of variable and constant terms increases, so do the number of steps it takes to solve the equation.

Examples

Solve: [latex]7x+5=6x+2[/latex]

Show Answer

Solve: [latex]6n - 2=-3n+7[/latex]

Show Answer

In the following video we show an example of how to solve a multi-step equation by moving the variable terms to one side and the constants to the other side. You will see that it doesn’t matter which side you choose to be the variable side; you can get the correct answer either way.

In the next example, we move the variable terms to the right side to keep a positive coefficient on the variable.

EXAMPLE

Solve: [latex]2a - 7=5a+8[/latex]

Show Answer

The following video shows another example of solving a multi-step equation by moving the variable terms to one side and the constants to the other side.

Try these problems to see how well you understand how to solve linear equations with variables and constants on both sides of the equal sign.

try it

Here is a much more complex multi-step equation.

EXAMPLE

Solve: [latex]\Large{\frac{x+22}{3}}=2x+4[/latex]

	[latex]\frac{x+22}{3}=2x+4[/latex]
Multiply both sides of the equation by 3	[latex]\color{red}{3}\cdot\frac{x+22}{3}=(2x+4)\color{red}{3}[/latex]
Eliminate the [latex]\frac{3}{3} = 1[/latex] on the left and Distribute on the right	[latex]x+22=\color{red}{3}(2x)+\color{red}{3}(4)[/latex]
Multiply	[latex]x+22=6x+12[/latex]
Subtract [latex]x[/latex] from both sides (keeps variable term positive)	[latex]22=5x+12[/latex]
Subtract [latex]12[/latex] from both sides (isolates the variable term)	[latex]10=5x[/latex]
Divide both sides by [latex]5[/latex] (isolates the variable)	[latex]2=x[/latex]
Rewrite solution with variable on the right	[latex]x=2[/latex]

The solution is [latex]x=2[/latex]
Check:	[latex]\frac{x+22}{3}=2x+4[/latex]
Let [latex]x=-11[/latex].	[latex]\frac{\color{red}{2}+22}{3}=2(\color{red}{2})+4[/latex]
	[latex]\frac{24}{3}\stackrel{\text{?}}{=}4+4[/latex]
	[latex]8=8\quad\checkmark[/latex]

We just showed a lot of examples of different kinds of linear equations you may encounter. There are some good habits to develop that will help you solve all kinds of linear equations. We’ll summarize the steps we took so you can easily refer to them.

Solve an equation with variables and constants on both sides

Choose one side to be the variable side and then the other will be the constant side.
Collect the variable terms to the variable side, using the Addition or Subtraction Property of Equality.
Collect the constants to the other side, using the Addition or Subtraction Property of Equality.
Make the coefficient of the variable [latex]1[/latex], using the Multiplication or Division Property of Equality.
Check the solution by substituting it into the original equation.

Contribute!

Did you have an idea for improving this content? We’d love your input.

Improve this page Learn More

	[latex]11-20=17y-8y-6y[/latex]
Simplify each side.	[latex]-9=3y[/latex]
Divide both sides by 3 to isolate y.	[latex]\Large\frac{-9}{\color{red}{3}}\normalsize =\Large\frac{3y}{\color{red}{3}}[/latex]
Simplify.	[latex]-3=y[/latex]
Check your answer. Let [latex]y=-3[/latex]
[latex]11-20=17y-8y-6y[/latex]
[latex]11-20\stackrel{\text{?}}{=}17( \color{red}{-3})-8(\color{red}{-3})-6(\color{red}{-3})[/latex]
[latex]11-20\stackrel{\text{?}}{=}-51+24+18[/latex]
[latex]-9=-9\quad\checkmark[/latex]

	[latex]-3(n-2)-6=21[/latex]
Distribute.	[latex]-3n+6-6=21[/latex]
Simplify.	[latex]-3n=21[/latex]
Divide both sides by -3 to isolate n.	[latex]\Large\frac{-3n}{\color{red}{-3}}\normalsize =\Large\frac{21}{\color{red}{-3}}[/latex] [latex]n=-7[/latex]
Check your answer. Let [latex]n=-7[/latex] .
[latex]-3(n-2)-6=21[/latex]
[latex]-3(\color{red}{-7}-2)-6\stackrel{\text{?}}{=}21[/latex]
[latex]-3(-9)-6\stackrel{\text{?}}{=}21[/latex]
[latex]27-6\stackrel{\text{?}}{=}21[/latex]
[latex]21=21\quad\checkmark[/latex]

[latex]5x[/latex] is the side containing only a variable. [latex]4x+7[/latex] is the side containing a constant.
We don’t want any variables on the right, so subtract the [latex]4x[/latex] .		[latex]5x\color{red}{-4x}=4x\color{red}{-4x}+7[/latex]
Simplify.		[latex]x=7[/latex]
We have all the variables on one side and the constants on the other. We have solved the equation.
Check:		[latex]5x=4x+7[/latex]
Substitute [latex]7[/latex] for [latex]x[/latex] .		[latex]5(\color{red}{7})\stackrel{\text{?}}{=}4(\color{red}{7})+7[/latex]
		[latex]35\stackrel{\text{?}}{=}28+7[/latex]
		[latex]35=35\quad\checkmark[/latex]

[latex]7x[/latex] is the side containing only a variable. [latex]-x+24[/latex] is the side containing a constant.
Remove the [latex]-x[/latex] from the right side by adding [latex]x[/latex] to both sides.	[latex]7x\color{red}{+x}=-x\color{red}{+x}+24[/latex]
Simplify.	[latex]8x=24[/latex]
All the variables are on the left and the constants are on the right. Divide both sides by [latex]8[/latex].	[latex]\Large\frac{8x}{\color{red}{8}}\normalsize =\Large\frac{24}{\color{red}{8}}[/latex]
Simplify.	[latex]x=3[/latex]
Check:	[latex]7x=-x+24[/latex]
Substitute [latex]x=3[/latex].	[latex]7(\color{red}{3})\stackrel{\text{?}}{=}-(\color{red}{3})+24[/latex]
	[latex]21=21\quad\checkmark[/latex]

[latex]5y-8[/latex] is the side containing a constant. [latex]7y[/latex] is the side containing only a variable.
Subtract [latex]5y[/latex] from both sides.	[latex]5y\color{red}{-5y}-8=7y\color{red}{-5y}[/latex]
Simplify.	[latex]-8=2y[/latex]
We have the variables on the right and the constants on the left. Divide both sides by [latex]2[/latex].	[latex]\Large\frac{-8}{\color{red}{2}}\normalsize =\Large\frac{2y}{\color{red}{2}}[/latex]
Simplify.	[latex]-4=y[/latex]
Rewrite with the variable on the left.	[latex]y=-4[/latex]
Check:	[latex]5y-8=7y[/latex]
Let [latex]y=-4[/latex].	[latex]5(\color{red}{-4})-8\stackrel{\text{?}}{=}7(\color{red}{-4})[/latex]
	[latex]-20-8\stackrel{\text{?}}{=}-28[/latex]
	[latex]-28=-28\quad\checkmark[/latex]

	[latex]7x+5=6x+2[/latex]
Collect the variable terms to the left side by subtracting [latex]6x[/latex] from both sides.	[latex]7x\color{red}{-6x}+5=6x\color{red}{-6x}+2[/latex]
Simplify.	[latex]x+5=2[/latex]
Now, collect the constants to the right side by subtracting [latex]5[/latex] from both sides.	[latex]x+5\color{red}{-5}=2\color{red}{-5}[/latex]
Simplify.	[latex]x=-3[/latex]
The solution is [latex]x=-3[/latex] .
Check:	[latex]7x+5=6x+2[/latex]
Let [latex]x=-3[/latex].	[latex]7(\color{red}{-3})+5\stackrel{\text{?}}{=}6(\color{red}{-3})+2[/latex]
	[latex]-21+5\stackrel{\text{?}}{=}-18+2[/latex]
	[latex]16=16\quad\checkmark[/latex]

	[latex]6n-2=-3n+7[/latex]
We don’t want variables on the right side—add [latex]3n[/latex] to both sides to leave only constants on the right.	[latex]6n\color{red}{+3n}-2=-3n\color{red}{+3n}+7[/latex]
Combine like terms.	[latex]9n-2=7[/latex]
We don’t want any constants on the left side, so add [latex]2[/latex] to both sides.	[latex]9n-2\color{red}{+2}=7\color{red}{+2}[/latex]
Simplify.	[latex]9n=9[/latex]
The variable term is on the left and the constant term is on the right. To get the coefficient of [latex]n[/latex] to be one, divide both sides by [latex]9[/latex].	[latex]\Large\frac{9n}{\color{red}{9}}\normalsize =\Large\frac{9}{\color{red}{9}}[/latex]
Simplify.	[latex]n=1[/latex]
Check:	[latex]6n-2=-3n+7[/latex]
Substitute [latex]1[/latex] for [latex]n[/latex].	[latex]6(\color{red}{1})-2\stackrel{\text{?}}{=}-3(\color{red}{1})+7[/latex]
	[latex]4=4\quad\checkmark[/latex]

	[latex]2a-7=5a+8[/latex]
Subtract [latex]2a[/latex] from both sides to remove the variable term from the left.	[latex]2a\color{red}{-2a}-7=5a\color{red}{-2a}+8[/latex]
Combine like terms.	[latex]-7=3a+8[/latex]
Subtract [latex]8[/latex] from both sides to remove the constant from the right.	[latex]-7\color{red}{-8}=3a+8\color{red}{-8}[/latex]
Simplify.	[latex]-15=3a[/latex]
Divide both sides by [latex]3[/latex] to make [latex]1[/latex] the coefficient of [latex]a[/latex] .	[latex]\Large\frac{-15}{\color{red}{3}}\normalsize =\Large\frac{3a}{\color{red}{3}}[/latex]
Simplify.	[latex]-5=a[/latex]
Check:	[latex]2a-7=5a+8[/latex]
Let [latex]a=-5[/latex]	[latex]2(\color{red}{-5})-7\stackrel{\text{?}}{=}5(\color{red}{-5})+8[/latex]
	[latex]-10-7\stackrel{\text{?}}{=}-25+8[/latex]
	[latex]-17=-17\quad\checkmark[/latex]

Module 2: Calculations and Solving Equations

Learning outcome

Example

TRY IT

Example

Try it

example

try it

Distributive Property

example

try it

example

try it

ExampleS

try it

example

try it

Solve Equations with Variables and Constants on Both Sides

Examples

EXAMPLE

try it

EXAMPLE

Solve an equation with variables and constants on both sides

Contribute!