There are multiple methods of solving systems of linear equations. For a system of linear equations in two variables, we can determine both the type of system and the solution by graphing the system of equations on the same set of axes.
We will practice graphing two equations on the same set of axes, and then we will explore the different considerations you need to make when graphing two linear inequalities on the same set of axes. The same techniques are used to graph a system of linear equations as you have used to graph single linear equations. We can use tables of values, slope and [latex]y[/latex]-intercept, or [latex]x[/latex]– and [latex]y[/latex]-intercepts to graph both lines on the same set of axes.
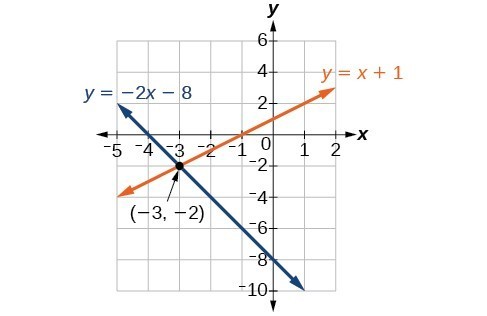
Example
Solve the following system of equations by graphing. Identify the type of system.
Graph both equations on the same set of axes as seen below.
The lines appear to intersect at the point [latex]\left(-3,-2\right)[/latex]. We can check to make sure that this is the solution to the system by substituting the ordered pair into both equations
The solution to the system is the ordered pair [latex]\left(-3,-2\right)[/latex], so the system is independent.
You can watch the video below for another example of how to solve a system of equations by first graphing the lines and then identifying the solution the system has.
Try It
In the following example, you will be given a system to graph that consists of two parallel lines.
Example
Graph the system [latex]\begin{array}{c}y=2x+1\\y=2x-3\end{array}[/latex] using the slopes and [latex]y[/latex]-intercepts of the lines.
Show Solution
First, graph [latex]y=2x+1[/latex] using the slope [latex]m = 2[/latex] and the [latex]y[/latex]-intercept [latex](0,1)[/latex]
Next, add [latex]y=2x-3[/latex] using the slope [latex]m = 2[/latex], and the [latex]y[/latex]-intercept [latex](0,-3)[/latex]
Notice how these are parallel lines, and they don’t cross. In the previous section, we discussed how there are no solutions to a system of equations that are parallel lines. We classified this type of system as an inconsistent system.
In the next example, you will be given a system whose equations look different, but after graphing, turn out to be the same line.
Example
Graph the system [latex]\begin{array}{c}y=\frac{1}{2}x+2\\2y-x=4\end{array}[/latex] using the x – and y-intercepts.
Show Solution
First, find the [latex]x[/latex]– and [latex]y[/latex]– intercepts of [latex]y=\frac{1}{2}x+2[/latex]
The [latex]x[/latex]-intercept will have a value of [latex]0[/latex] for [latex]y[/latex], so substitute [latex]y=0[/latex] into the equation, and isolate the variable [latex]x[/latex].
The [latex]x[/latex]-intercept of [latex]y=\frac{1}{2}x+2[/latex] is [latex]\left(-4,0\right)[/latex].
The [latex]y[/latex]-intercept is easier to find since this equation is in slope-intercept form. The [latex]y[/latex]-intercept is [latex](2,0)[/latex].
Now we can plot [latex]y=\frac{1}{2}x+2[/latex] using the intercepts
Now find the intercepts of [latex]2y-x=4[/latex]
Substitute [latex]y = 0[/latex] in to the equation to find the [latex]x[/latex]-intercept.
The [latex]y[/latex]-intercept of [latex]2y-x=4[/latex] is [latex]\left(0,2\right)[/latex].
WAIT, these are the same intercepts as [latex]y=\frac{1}{2}x+2[/latex]! In fact, [latex]y=\frac{1}{2}x+2[/latex] and [latex]2y-x=4[/latex] are really the same equation, expressed in different ways. If you were to write them both in slope-intercept form you would see that they are the same equation.
When you graph them, they are the same line. In the previous section, we learned that systems with two of the same equations in them have an infinite number of solutions and are classified as a dependent system.
As demonstrated by the examples above, graphing can be used if the system is inconsistent or dependent. In both cases, we can still graph the system to determine the type of system and solution. If the two lines are parallel, the system has no solution and is inconsistent. If the two lines are identical, the system has infinite solutions and is a dependent system.
The video below provides more examples of how to graph systems of linear equations.
Graphing a system of linear equations consists of choosing which graphing method you want to use and drawing the graphs of both equations on the same set of axes.
Contribute!
Did you have an idea for improving this content? We’d love your input.
Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: . License: CC BY: Attribution
Ex 1: Graph a System of Linear Inequalities Mathispower4u Mathispower4u. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/ACTxJv1h2_c. License: CC BY: Attribution
