Learning Outcomes
- Classify solutions for systems
Some linear systems may not have a solution and others may have an infinite number of solutions. In order for a linear system to have a unique solution, there must be at least as many equations as there are variables. Even so, this does not guarantee a unique solution.
Use a graph to classify solutions to systems
Recall that a linear equation graphs as a line, which indicates that all of the points on the line are solutions to that linear equation. There are an infinite number of solutions. As we saw in the last section, if you have a system of linear equations that intersect at one point, this point is a solution to the system. What happens if the lines never cross, as in the case of parallel lines? How would you describe the solutions to that kind of system? In this section, we will explore the three possible outcomes for solutions to a system of linear equations.
Three possible outcomes for solutions to systems of equations
Recall that the solution for a system of equations is the value or values that are true for all equations in the system. There are three possible outcomes for solutions to systems of linear equations. The graphs of equations within a system can tell you how many solutions exist for that system. Look at the images below. Each shows two lines that make up a system of equations.
| One Solution | No Solutions | Infinite Solutions |
|---|---|---|
 |
 |
 |
| If the graphs of the equations intersect, then there is one solution that is true for both equations. | If the graphs of the equations do not intersect (for example, if they are parallel), then there are no solutions that are true for both equations. | If the graphs of the equations are the same, then there are an infinite number of solutions that are true for both equations. |
- One Solution: When a system of equations intersects at an ordered pair, the system has one solution.
- Infinite Solutions: Sometimes the two equations will graph as the same line, in which case we have an infinite number of solutions.
- No Solution: When the lines that make up a system are parallel, there are no solutions because the two lines share no points in common.
Example
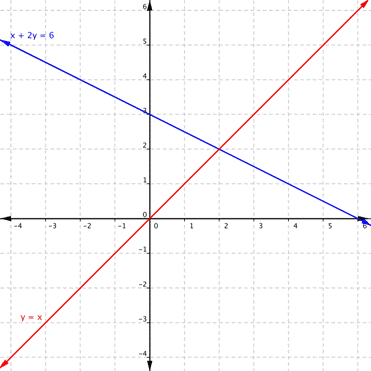
Using the graph of [latex]\begin{array}{r}y=x\\x+2y=6\end{array}[/latex], shown below, determine how many solutions the system has.
Example (Advanced)
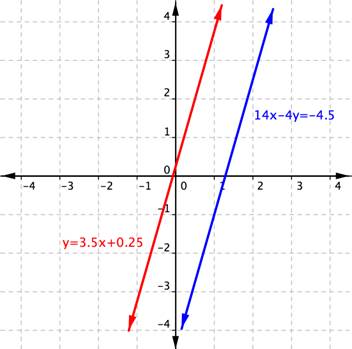
Using the graph of [latex]\begin{array}{r}y=3.5x+0.25\\14x–4y=-4.5\end{array}[/latex], shown below, determine how many solutions the system has.
Example
How many solutions does the system [latex]\begin{array}{r}y=2x+1\\−4x+2y=2\end{array}[/latex] have?
Because the number of solutions that a system of equations has is so important, we actually have special categories of systems of linear equations based upon the number of solutions a system has. A consistent system of equations has at least one solution. A consistent system is considered to be an independent system if it has a single solution like the first example we explored. The two lines have different slopes and intersect at one point in the plane. A consistent system is considered to be a dependent system if there are an infinite number of solutions, like in the third example we explored. A system of equations is dependent if the equations have the same slope and the same y-intercepts. In other words, the lines coincide, so the equations represent the same line and every point on the line represents a coordinate pair that satisfies the system.
Another type of system of linear equations is an inconsistent system, which is when there are no points common to both lines and, hence, there is no solution to the system, like in the second example we explored. In an inconsistent system, the equations represent two parallel lines that have the same slope and different y-intercepts.
A General Note: Types of Linear Systems
There are three types of systems of linear equations in two variables and three types of solutions.
- An independent system has exactly one solution pair [latex]\left(x,y\right)[/latex]. The point where the two lines intersect is the only solution.
- An inconsistent system has no solution.The two lines are parallel and will never intersect.
- A dependent system has infinitely many solutions. The lines are coincident. They are the same line, so every coordinate pair on the line is a solution to both equations.
Below are graphical representations of each type of system.
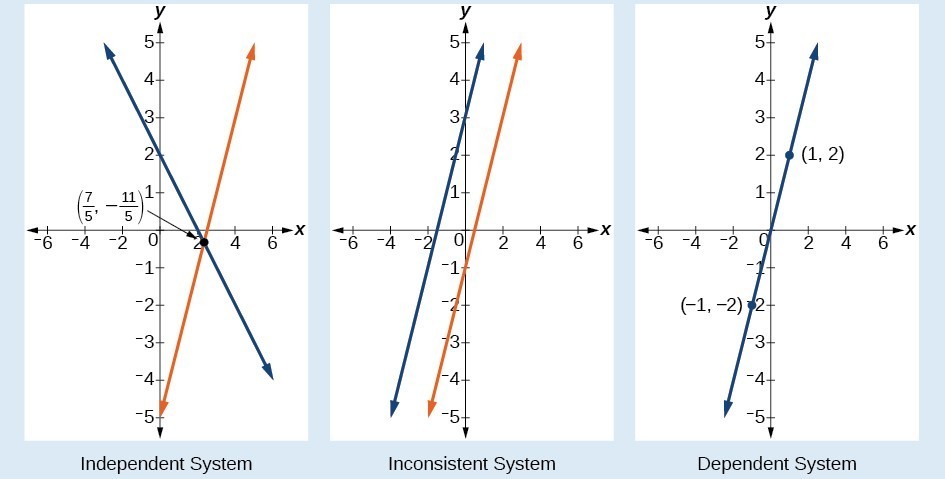
The independent and dependent systems are also consistent because they both have at least one solution.
