Learning Outcomes
- Evaluate ordered pairs as solutions to systems
A system of linear equations consists of two or more linear equations made up of two or more variables such that all equations in the system are considered simultaneously. To find the unique solution to a system of linear equations, we must find a numerical value for each variable in the system that will satisfy all equations in the system at the same time.
Determine whether an ordered pair is a solution for a system of linear equations
In this section, we will look at systems of linear equations in two variables which consist of two equations that each contain two different variables. For example, consider the following system of linear equations in two variables.
The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. In this example, the ordered pair [latex](4, 7)[/latex] is the solution to the system of linear equations. We can verify the solution by substituting the values into each equation to see if the ordered pair satisfies both equations. Shortly, we will investigate methods of finding such a solution if it exists.
How To: Given a system of linear equations and an ordered pair, determine whether the ordered pair is a solution
- Substitute the ordered pair into each equation in the system.
- Determine whether true statements result from the substitution in both equations; if so, the ordered pair is a solution.
The lines in the graph above are defined as
[latex]\begin{array}{r}2x-y=-4\\ x-y=-1\end{array}[/latex].
They cross at what appears to be [latex]\left(-3,-2\right)[/latex].
Using algebra, we can verify that this shared point is actually [latex]\left(-3,-2\right)[/latex] and not [latex]\left(-2.999,-1.999\right)[/latex]. By substituting the [latex]x[/latex]– and [latex]y[/latex]-values of the ordered pair into the equation of each line, you can test whether the point is on both lines. If the substitution results in a true statement, then you have found a solution to the system of equations!
Since the solution of the system must be a solution to all the equations in the system, you will need to check the point in each equation. In the following example, we will substitute [latex]-3[/latex] for [latex]x[/latex] and [latex]-2[/latex] for [latex]y[/latex] in each equation to test whether it is actually the solution.
Example
Is [latex]\left(-3,-2\right)[/latex] a solution of the system
[latex]\begin{array}{r}2x-y=-4\\ x-y=-1\end{array}[/latex]
Example
Is [latex](3, 9)[/latex] a solution of the system
[latex]\begin{array}{r}y=3x\\2x–y=6\end{array}[/latex]
Example
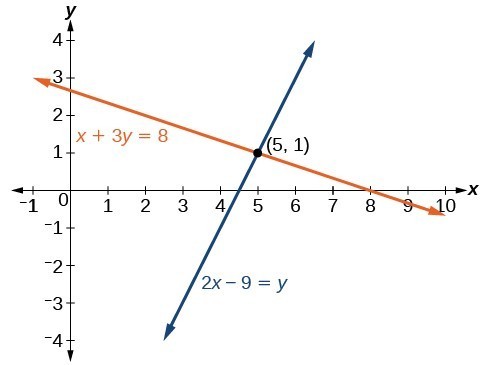
Determine whether the ordered pair [latex]\left(5,1\right)[/latex] is a solution to the given system of equations.
Think About It
Is [latex](−2,4)[/latex] a solution for the system
[latex]\begin{array}{r}y=2x\\3x+2y=1\end{array}[/latex]
Before you do any calculations, look at the point given and the first equation in the system. Can you predict the answer to the question without doing any algebra?
In the following video, we will show another example of how to verify whether an ordered pair is a solution to a system of equations.
Remember that in order to be a solution to the system of equations, the values of the point must be a solution for both equations. Once you find one equation for which the point is false, you have determined that it is not a solution for the system.
