Learning Outcomes
- Recognize a quadratic equation
- Use the zero product principle to solve a quadratic equation that can be factored
When a polynomial is set equal to a value (whether an integer or another polynomial), the result is an equation. An equation that can be written in the form [latex]ax^{2}+bx+c=0[/latex] is called a quadratic equation. When solving polynomials where the highest degree is degree 2, we want to confirm that the equation is written in standard form, [latex]a{x}^{2}+bx+c=0[/latex], where a, b, and c are real numbers and [latex]a\ne 0[/latex]. The equation [latex]{x}^{2}+x - 6=0[/latex] is in standard form.
Quadratic Equation
A quadratic equation is an equation containing a second-degree polynomial; for example,
where a, b, and c are real numbers, and if [latex]a\ne 0[/latex], it is in standard form.
Often the easiest method of solving a quadratic equation is by factoring. Factoring means finding expressions that can be multiplied together to give the expression on one side of the equation. Note that we will not spend a lot of time explaining how to factor in this section. We cover factoring in an earlier module of this course and you can sharpen your skills there.
Solving by factoring depends on the Principle of Zero Products. What if we told you that we multiplied two numbers together and got an answer of zero? What could you say about the two numbers? Could they be [latex]2[/latex] and [latex]5[/latex]? Could they be [latex]9[/latex] and [latex]1[/latex]? No! When the result (answer) from multiplying two numbers is zero, that means that one of them had to be zero. This idea is called the zero product principle, and it is useful for solving polynomial equations that can be factored. You can further review the Principle of Zero Products here.
Principle of Zero Products
The Principle of Zero Products states that if the product of two numbers is [latex]0[/latex], then at least one of the factors is [latex]0[/latex]. If [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both a and b are [latex]0[/latex].
In this section, we will show several examples of solving quadratic equations using factoring. For each example, we will be using the same general technique:
How to solve a quadratic equation using factoring
- Make sure your quadratic equation is written in standard form, that is, [latex]a{x}^{2}+bx+c=0[/latex] where a, b, and c are real numbers, and [latex]a\ne 0[/latex].
- Factor the quadratic expression on the left-hand side of the equation.
- Solve using the zero-product property by setting each factor equal to zero and solving for the variable.
Let us start with a simple example. We will factor a GCF from a binomial and apply the principle of zero products to solve a polynomial equation. (You can review how to factor out a greatest common factor here)
Example
Solve:
[latex]-t^2+t=0[/latex]
In the following video, we show two more examples of using both factoring and the principle of zero products to solve a polynomial equation.
In our next example, we will solve a quadratic equation that has a leading coefficient of 1. In the quadratic equation [latex]{x}^{2}+x - 6=0[/latex], the leading coefficient, or the coefficient of [latex]{x}^{2}[/latex], is [latex]1[/latex]. Notice that if we compare this equation to the standard form of a quadratic equation, then [latex]a=1[/latex], [latex]b=1[/latex], and [latex]c=-b[/latex]. For a review on how to factor a quadratic polynomial with a leading coefficient of 1, you can visit this page.
Example
Factor and solve the equation: [latex]{x}^{2}+x - 6=0[/latex].
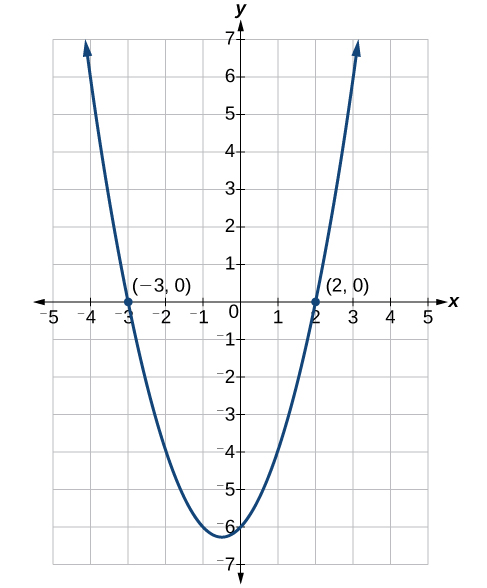
If we graph the equation [latex]y={x}^{2}+x - 6[/latex], we will get the parabola in the figure below (NOTE: we will learn how to graph quadratic equations in greater detail when we learn about functions). The solutions to the equation [latex]{x}^{2}+x - 6=0[/latex] are the x-intercepts of [latex]y={x}^{2}+x - 6[/latex]. Recall that x-intercepts are where the y values are zero, therefore the points [latex](-3,0)[/latex] and [latex](2,0)[/latex] represent the places where the parabola crosses the x-axis. This matches up with our solution to the equation [latex]{x}^{2}+x - 6=0[/latex] because it shows that when [latex]x=2[/latex] and [latex]x=-3[/latex], our equation equals [latex]0[/latex]
In the following video, we provide more examples of factoring to solve quadratic equations where the leading coefficient is equal to 1.
Try It
We all know that it is rare to be given an equation to solve that has zero on one side, so let us try an example where we first have to move all the terms of the equation to the left-hand side.
Example
Solve: [latex]s^2-4s=5[/latex]
In our next example, we solve a quadratic equation with a leading coefficient that is not equal to 1. Recall that when the leading coefficient is not [latex]1[/latex], we factor a quadratic equation using a method called grouping, which requires four terms. You can review how to factor by grouping here.
Example
Solve the quadratic equation: [latex]4{x}^{2}+15x+9=0[/latex].
The example below shows a quadratic equation where neither side is originally equal to zero. Remember, we cannot solve quadratic equations unless one side is equal to zero because this allows us to use the Zero Product Principle. (Note that the factoring sequence has been shortened.)
Example
Solve [latex]5b^{2}+4=−12b[/latex] for b.
We will work through one more example that is similar to the one above, except this example has fractions, yay!
Example
Solve [latex]y^2-5=-\frac{7}{2}y+\frac{5}{2}[/latex]
In our last video, we show how to solve another quadratic equation that contains fractions.
The following video contains another example of solving a quadratic equation using factoring with grouping.
It is useful to remember that, if you factor out a constant, the constant will never equal [latex]0[/latex]. So it can essentially be ignored when solving. See the following example.
Example
Solve for k: [latex]-2k^2+90=-8k[/latex]
We can use the zero-product property to solve quadratic equations in which we first have to factor out the greatest common factor (GCF) and for equations that have special factoring formulas as well, such as the difference of squares, which we will see later in this section.
In our next example, we will solve a quadratic equation that is written as a difference of squares. For a review of difference of squares and other special cases, you can visit this page.
Example
Solve the difference of squares equation using the zero-product property: [latex]{x}^{2}-9=0[/latex].
Sometimes, we may be given an equation that does not look like a quadratic at first glance. In our next examples we will solve a cubic polynomial equation where the GCF of each term is x and can be factored. The result is a quadratic equation that we can solve.
Example
Solve the equation by factoring: [latex]-3{x}^{3}-5{x}^{2}-2x=0[/latex].
In this last video example, we solve a quadratic equation with a leading coefficient of -1 using a shortcut method of factoring and the zero product principle.
Summary
You can find the solutions, or roots, of quadratic equations by setting one side equal to zero, factoring the polynomial, and then applying the Zero Product Property. The Principle of Zero Products states that if [latex]ab=0[/latex], then either [latex]a=0[/latex] or [latex]b=0[/latex], or both a and b are [latex]0[/latex]. Once the polynomial is factored, set each factor equal to zero and solve them separately. The answers will be the set of solutions for the original equation.
Candela Citations
- Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
- Ex 2: Quadratic Equation App - Find the Dimensions of a Rectangle Given Area (Factoring). Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/PvXsWZp588o. License: CC BY: Attribution
- Ex: Solve a Quadratic Equation Using Factor By Grouping. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/04zEXaOiO4U. License: CC BY: Attribution
- Ex: Factor and Solve Quadratic Equation - Trinomial a = -1. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/nZYfgHygXis. License: CC BY: Attribution
- Unit 12: Factoring, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution