Quadratic equations can be solved using many methods. You may already be familiar with factoring to solve some quadratic equations. However, not all quadratic equations can be factored. In this section, you will use square roots to learn another way to solve quadratic equations—and this method will work with all quadratic equations.

Solve a Quadratic Equation by the Square Root Property

One way to solve the quadratic equation [latex]x^{2}=9[/latex] is to subtract [latex]9[/latex] from both sides to get one side equal to 0: [latex]x^{2}-9=0[/latex]. The expression on the left can be factored; it is a difference of squares: [latex]\left(x+3\right)\left(x–3\right)=0[/latex]. Using the zero factor property, you know this means [latex]x+3=0[/latex] or [latex]x–3=0[/latex], so [latex]x=−3[/latex] or [latex]3[/latex].

Another property that would let you solve this equation more easily is called the square root property.

A shortcut way to write “[latex] \sqrt{a}[/latex]” or “[latex] -\sqrt{a}[/latex]” is [latex] \pm \sqrt{a}[/latex]. The symbol [latex]\pm[/latex] is often read “positive or negative.” If it is used as an operation (addition or subtraction), it is read “plus or minus.”

Notice that there is a difference here in solving [latex]x^{2}=9[/latex] and finding [latex] \sqrt{9}[/latex]. For [latex]x^{2}=9[/latex], you are looking for all numbers whose square is [latex]9[/latex]. For [latex] \sqrt{9}[/latex], you only want the principal (nonnegative) square root. The negative of the principal square root is [latex] -\sqrt{9}[/latex]; both would be [latex] \pm \sqrt{9}[/latex]. Unless there is a symbol in front of the radical sign, only the nonnegative value is wanted!

In the example above, you can take the square root of both sides easily because there is only one term on each side. In some equations, you may need to do some work to get the equation in this form. You will find that this involves isolating [latex]x^{2}[/latex].

In our first video, we will show more examples of using the square root property to solve a quadratic equation.

Sometimes more than just the [latex]x[/latex] is being squared:

In the next video, you will see more examples of using square roots to solve quadratic equations.

Solve a Quadratic Equation by Completing the Square

Not all quadratic equations can be factored or solved in their original form using the square root property. In these cases, we may use a method for solving a quadratic equation known as completing the square. Using this method, we add or subtract terms to both sides of the equation until we have a perfect square trinomial on one side of the equal sign. We then apply the square root property.

Some of the above examples have squared binomials: [latex]\left(1+r\right)^{2}[/latex] and [latex]\left(x–2\right)^{2}[/latex] are squared binomials. If you expand these, you get a perfect square trinomial.

Perfect square trinomials have the form [latex]x^{2}+2xs+s^{2}[/latex] and can be factored as [latex]\left(x+s\right)^{2}[/latex], or they have the form [latex]x^{2}–2xs+s^{2}[/latex] and can be factored as [latex]\left(x–s\right)^{2}[/latex]. Let’s factor a perfect square trinomial into a squared binomial.

If this were an equation, we could solve using either the square root property or the zero product property.

You can use the same procedure in this next example to help you solve equations where you identify perfect square trinomials, even if the equation is not set equal to [latex]0[/latex].

One way to solve quadratic equations is by completing the square. When you don’t have a perfect square trinomial, you can create one by adding a constant term that is a perfect square to both sides of the equation. Let’s see how to find that constant term.

“Completing the square” does exactly what it says—it takes something that is not a square and makes it one. This idea can be illustrated using an area model of the binomial [latex]x^{2}+bx[/latex].

In this example, the area of the overall rectangle is given by [latex]x\left(x+b\right)[/latex].

Now let’s make this rectangle into a square. First, divide the red rectangle with area bx into two equal rectangles each with area [latex] \frac{b}{2}x[/latex]. Then rotate and reposition one of them. You haven’t changed the size of the red area—it still adds up to [latex]bx[/latex].

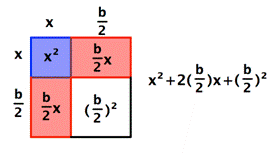The red rectangles now make up two sides of a square, shown in white. The area of that square is the length of the red rectangles squared, or [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex].

Here comes the cool part—do you see that when the white square is added to the blue and red regions, the whole shape is also now a square? In other words, you’ve “completed the square!” By adding the quantity [latex]\left(\frac{b}{2}\right)^{2}[/latex] to the original binomial, you’ve made a square, a square with sides of [latex]x+\frac{b}{2}[/latex].

Notice that the area of this square can be written as a squared binomial: [latex]\left(x+\frac{b}{2}\right)^{2}[/latex].

Notice that [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex] is always positive, since it is the square of a number. When you complete the square, you are always adding a positive value.

In the following video, we show more examples of how to find a constant term that will make a trinomial a perfect square.

You can use completing the square to help you solve a quadratic equation that cannot be solved by factoring (and it will still work even when you can factor!).

Let’s start by seeing what happens when you complete the square in an equation. In the example below, notice that completing the square will result in adding a number to both sides of the equation—you have to do this in order to keep both sides equal!

Can you see that completing the square in an equation is very similar to completing the square in an expression? The main difference is that you have to add the new number ([latex]+9[/latex] in this case) to both sides of the equation to maintain equality.

Now let’s look at an example where you are using completing the square to actually solve an equation, finding a value for the variable.

Notice that, to complete the square, the leading coefficient, a, must equal 1. If it does not, then divide the entire equation by a. Then, we can use the following procedures to solve a quadratic equation by completing the square.

In the next video, you will see more examples of how to use completing the square to solve a quadratic equation.

You may have noticed that because you have to use both square roots, all the examples have two solutions. Here is another example that is slightly different.

Take a closer look at this problem and you may see something familiar. Instead of completing the square, try adding [latex]47[/latex] to both sides in the equation. The equation [latex]x^{2}+16x+17=−47[/latex] becomes [latex]x^{2}+16x+64=0[/latex]. Can you factor this equation using grouping? (Think of two numbers whose product is 64 and whose sum is [latex]16[/latex]).

It can be factored as [latex](x+8)(x+8)=0[/latex], of course! Knowing how to complete the square is very helpful, but it is not always the only way to solve an equation.

In our last video, we show an example of how to use completing the square to solve a quadratic equation whose solutions are irrational.

Summary

Completing the square is used to change a binomial of the form [latex]x^{2}+bx[/latex] into a perfect square trinomial [latex] {{x}^{2}}+bx+{{\left( \frac{b}{2} \right)}^{2}}[/latex] which can be factored to [latex] {{\left( x+\frac{b}{2} \right)}^{2}}[/latex]. When solving quadratic equations by completing the square, be careful to add [latex] {{\left( \frac{b}{2} \right)}^{2}}[/latex] to both sides of the equation to maintain equality. The Square Root Property can then be used to solve for [latex]x[/latex]. With the Square Root Property, be careful to include both the principal square root and its opposite. Be sure to simplify as needed.

Contribute!

Improve this pageLearn More