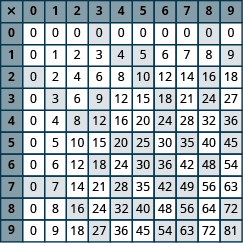
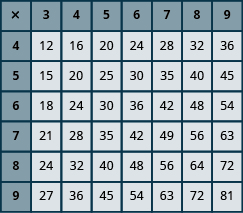
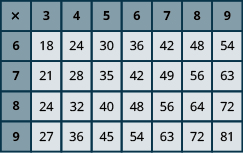
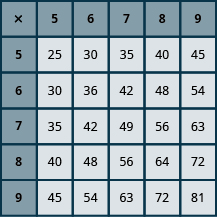
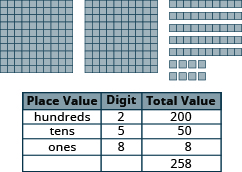
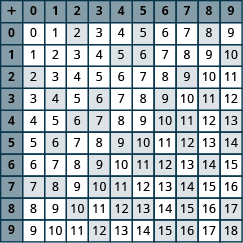
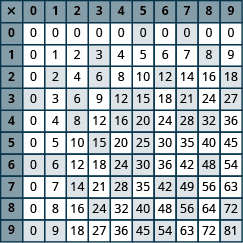
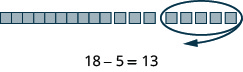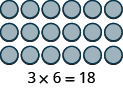Introduction to Whole Number Basics
Identify Counting Numbers and Whole Numbers
In the following exercises, determine which of the following numbers are a) counting numbers and b) whole numbers.
- [latex]0,\frac{2}{3},5,8.1,125[/latex]
Show Solution
- [latex]0,\frac{7}{10},3,20.5,300[/latex]
- [latex]0,\frac{4}{9},3.9,50,221[/latex]
Show Solution
- [latex]0,\frac{3}{5},10,303,422.6[/latex]
Model Whole Numbers
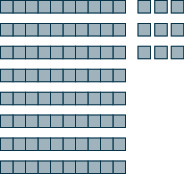
In the following exercises, use place value notation to find the value of the number modeled by the [latex]\text{base -10}[/latex] blocks.
Exercise 1
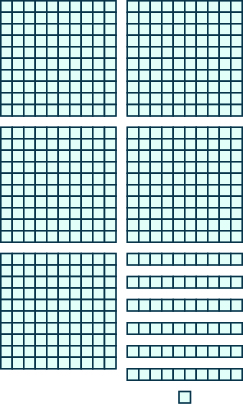
Exercise 2
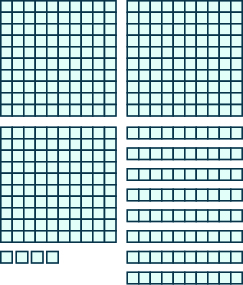
Exercise 3
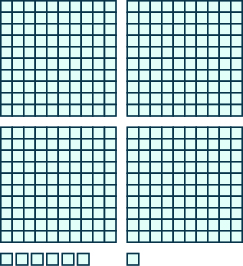
Exercises 4

Identify the Place Value of a Digit
In the following exercises, find the place value of the given digits.
Exercise 1
[latex]579,601[/latex]
- 9
- 6
- 0
- 7
- 5
Exercise 2
[latex]398,127[/latex]
- 9
- 3
- 2
- 8
- 7
Exercise 3
[latex]56,804,379[/latex]
- 8
- 6
- 4
- 7
- 0
Exercise 4
[latex]78,320,465[/latex]
- 8
- 4
- 2
- 6
- 7
Use Place Value to Name Whole Numbers
In the following exercises, name each number in words.
Exercise 1
- [latex]1,078[/latex]
Show Solution
- [latex]5,902[/latex]
- [latex]364,510[/latex]
Show Solution
- [latex]146,023[/latex]
- [latex]5,846,103[/latex]
Show Solution
- [latex]1,458,398[/latex]
- [latex]37,889,005[/latex]
Show Solution
- [latex]62,008,465[/latex]
Exercise 2
- The height of Mount Ranier is [latex]14,410[/latex] feet.
Show Solution
- The height of Mount Adams is [latex]12,276[/latex] feet.
- Seventy years is [latex]613,200[/latex] hours.
Show Solution
- One year is [latex]525,600[/latex] minutes.
- The U.S. Census estimate of the population of Miami-Dade county was [latex]2,617,176[/latex].
Show Solution
- The population of Chicago was [latex]2,718,782[/latex].
- There are projected to be [latex]23,867,000[/latex] college and university students in the US in five years.
Show Solution
- About twelve years ago there were [latex]20,665,415[/latex] registered automobiles in California.
- The population of China is expected to reach [latex]1,377,583,156[/latex] in [latex]2016[/latex].
Show Solution
- The population of India is estimated at [latex]1,267,401,849[/latex] as of July [latex]1,2014[/latex].
Use Place Value to Write Whole Numbers
In the following exercises, write each number as a whole number using digits.
- four hundred twelve
Show Solution
- two hundred fifty-three
- thirty-five thousand, nine hundred seventy-five
Show Solution
- sixty-one thousand, four hundred fifteen
- eleven million, forty-four thousand, one hundred sixty-seven
Show Solution
- eighteen million, one hundred two thousand, seven hundred eighty-three
- three billion, two hundred twenty-six million, five hundred twelve thousand, seventeen
Show Solution
- eleven billion, four hundred seventy-one million, thirty-six thousand, one hundred six
- The population of the world was estimated to be seven billion, one hundred seventy-three million people.
Show Solution
- The age of the solar system is estimated to be four billion, five hundred sixty-eight million years.
- Lake Tahoe has a capacity of thirty-nine trillion gallons of water.
Show Solution
- The federal government budget was three trillion, five hundred billion dollars.
Round Whole Numbers
In the following exercises, round to the indicated place value.
Round to the nearest ten:
- [latex]386[/latex]
Show Solution
- [latex]2,931[/latex]
Show Solution
Round to the nearest ten:
- [latex]792[/latex]
Show Solution
- [latex]5,647[/latex]
Show Solution
Round to the nearest hundred:
- [latex]13,748[/latex]
Show Solution
- [latex]391,794[/latex]
Show Solution
Round to the nearest hundred:
- [latex]28,166[/latex]
Show Solution
- [latex]481,628[/latex]
Show Solution
Round to the nearest ten:
- [latex]1,492[/latex]
Show Solution
- [latex]1,497[/latex]
Show Solution
Round to the nearest thousand:
- [latex]2,391[/latex]
Show Solution
- [latex]2,795[/latex]
Show Solution
Round to the nearest hundred:
- [latex]63,994[/latex]
Show Solution
- [latex]63,949[/latex]
Show Solution
Round to the nearest thousand:
- [latex]163,584[/latex]
Show Solution
- [latex]163,246[/latex]
Show Solution
Everyday Math
Writing a Check
Jorge bought a car for [latex]\$24,493[/latex]. He paid for the car with a check. Write the purchase price in words.
Writing a Check
Marissa’s kitchen remodeling cost [latex]\$18,549[/latex]. She wrote a check to the contractor. Write the amount paid in words.
Buying a Car
Jorge bought a car for [latex]\$24,493[/latex]. Round the price to the nearest:
- ten dollars
- hundred dollars
- thousand dollars
- ten-thousand dollars
Remodeling a Kitchen
Marissa’s kitchen remodeling cost [latex]\$18,549[/latex]. Round the cost to the nearest:
- ten dollars
- hundred dollars
- thousand dollars
- ten-thousand dollars
Population
The population of China was [latex]1,355,692,544[/latex] in 2014. Round the population to the nearest:
- billion people
- hundred-million people
- million people
Astronomy
The average distance between Earth and the sun is [latex]149,597,888[/latex] kilometers. Round the distance to the nearest:
- hundred-million kilometers
- ten-million kilometers
- million kilometers
Writing Exercises
In your own words, explain the difference between the counting numbers and the whole numbers.
Give an example from your everyday life where it helps to round numbers.
Adding Whole Numbers
Use Addition Notation
In the following exercises, translate the following from math expressions to words.
- [latex]5+2[/latex]
Show Solution
- [latex]6+3[/latex]
- [latex]13+18[/latex]
Show Solution
- [latex]15+16[/latex]
- [latex]214+642[/latex]
Show Solution
- [latex]438+113[/latex]
Model Addition of Whole Numbers
In the following exercises, model the addition.
- [latex]2+4[/latex]
Show Solution
- [latex]5+3[/latex]
- [latex]8+4[/latex]
Show Solution
- [latex]5+9[/latex]
- [latex]14+75[/latex]
Show Solution
- [latex]15+63[/latex]
- [latex]16+25[/latex]
Show Solution
- [latex]14+27[/latex]
Add Whole Numbers
In the following exercises, fill in the missing values in each chart.
Exercise 1
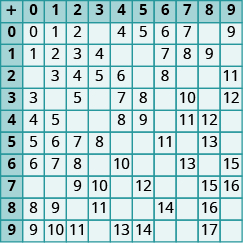
Exercise 2
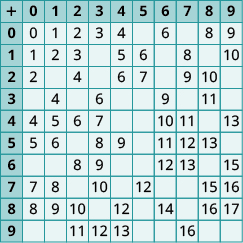
Exercises 3
Exercise 4
Exercise 5
Exercise 6
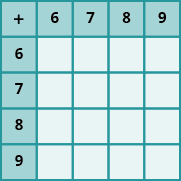
Add Whole Numbers
In the following exercises, add.
- [latex]0+13[/latex]
Show Solution
- [latex]13+0[/latex]
Show Solution
- [latex]0+5,280[/latex]
- [latex]5,280+0[/latex]
- [latex]8+3[/latex]
Show Solution
- [latex]3+8[/latex]
Show Solution
- [latex]7+5[/latex]
- [latex]5+7[/latex]
- [latex]45+33[/latex]
Show Solution
- [latex]37+22[/latex]
- [latex]71+28[/latex]
Show Solution
- [latex]43+53[/latex]
- [latex]26+59[/latex]
Show Solution
- [latex]38+17[/latex]
- [latex]64+78[/latex]
Show Solution
- [latex]92+39[/latex]
- [latex]168+325[/latex]
Show Solution
- [latex]247+149[/latex]
- [latex]584+277[/latex]
Show Solution
- [latex]175+648[/latex]
- [latex]832+199[/latex]
Show Solution
- [latex]775+369[/latex]
- [latex]6,358+492[/latex]
Show Solution
- [latex]9,184+578[/latex]
- [latex]3,740+18,593[/latex]
Show Solution
- [latex]6,118+15,990[/latex]
- [latex]485,012+619,848[/latex]
Show Solution
- [latex]368,911+857,289[/latex]
- [latex]24,731+592+3,868[/latex]
Show Solution
- [latex]28,925+817+4,593[/latex]
- [latex]8,015+76,946+16,570[/latex]
Show Solution
- [latex]6,291+54,107+28,635[/latex]
Translate Word Phrases to Math Notation
In the following exercises, translate each phrase into math notation and then simplify.
- the sum of [latex]13[/latex] and [latex]18[/latex]
Show Solution
- the sum of [latex]12[/latex] and [latex]19[/latex]
- the sum of [latex]90[/latex] and [latex]65[/latex]
Show Solution
- the sum of [latex]70[/latex] and [latex]38[/latex]
- [latex]33[/latex] increased by [latex]49[/latex]
Show Solution
- [latex]68[/latex] increased by [latex]25[/latex]
- [latex]250[/latex] more than [latex]599[/latex]
Show Solution
- [latex]115[/latex] more than [latex]286[/latex]
- the total of [latex]628[/latex] and [latex]77[/latex]
Show Solution
- the total of [latex]593[/latex] and [latex]79[/latex]
- [latex]1,482[/latex] added to [latex]915[/latex]
Show Solution
- [latex]2,719[/latex] added to [latex]682[/latex]
Add Whole Numbers in Applications
In the following exercises, solve the problem.
Home remodeling
Sophia remodeled her kitchen and bought a new range, microwave, and dishwasher. The range cost [latex]\$1,100[/latex], the microwave cost [latex]\$250[/latex], and the dishwasher cost [latex]\$525[/latex]. What was the total cost of these three appliances?
Sports equipment
Aiden bought a baseball bat, helmet, and glove. The bat cost [latex]\$299[/latex], the helmet cost [latex]\$35[/latex], and the glove cost [latex]\$68[/latex]. What was the total cost of Aiden’s sports equipment?
Bike riding
Ethan rode his bike [latex]14[/latex] miles on Monday, [latex]19[/latex] miles on Tuesday, [latex]12[/latex] miles on Wednesday, [latex]25[/latex] miles on Friday, and [latex]68[/latex] miles on Saturday. What was the total number of miles Ethan rode?
Business
Chloe has a flower shop. Last week she made [latex]19[/latex] floral arrangements on Monday, [latex]12[/latex] on Tuesday, [latex]23[/latex] on Wednesday, [latex]29[/latex] on Thursday, and [latex]44[/latex] on Friday. What was the total number of floral arrangements Chloe made?
Apartment size
Jackson lives in a 7 room apartment. The number of square feet in each room is [latex]238,120,156,196,100,132[/latex], and [latex]225[/latex]. What is the total number of square feet in all [latex]7[/latex] rooms?
Weight
Seven men rented a fishing boat. The weights of the men were [latex]175,192,148,169,205,181[/latex], and [latex]\text{225}[/latex] pounds. What was the total weight of the seven men?
Salary
Last year Natalie’s salary was [latex]\$82,572[/latex]. Two years ago, her salary was [latex]\$79,316[/latex], and three years ago it was [latex]\$75,298[/latex]. What is the total amount of Natalie’s salary for the past three years?
Home sales
Emma is a realtor. Last month, she sold three houses. The selling prices of the houses were [latex]\$292,540,\$505,875[/latex], and [latex]\$423,699[/latex]. What was the total of the three selling prices?
Finding Perimeter
In the following exercises, find the perimeter of each figure.
Exercise 1
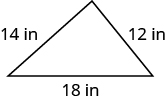
Exercise 2
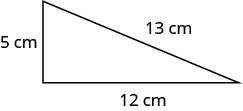
Exercise 3
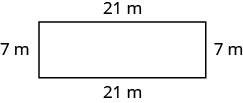
Exercise 4
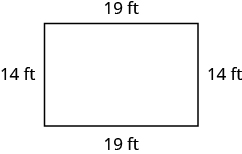
Exercise 5
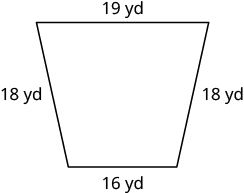
Exercise 6
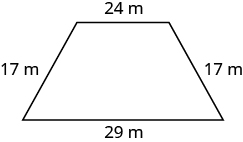
Exercise 7
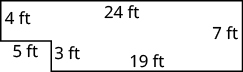
Exercise 8
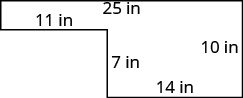
Everyday Math
Calories
Paulette had a grilled chicken salad, ranch dressing, and a [latex]\text{16-ounce}[/latex] drink for lunch. On the restaurant’s nutrition chart, she saw that each item had the following number of calories:
- Grilled chicken salad – [latex]320[/latex] calories
- Ranch dressing – [latex]170[/latex] calories
- [latex]\text{16-ounce}[/latex] drink – [latex]150[/latex] calories
What was the total number of calories of Paulette’s lunch?
Calories
Fred had a grilled chicken sandwich, a small order of fries, and a [latex]\text{12-oz}[/latex] chocolate shake for dinner. The restaurant’s nutrition chart lists the following calories for each item:
- Grilled chicken sandwich – [latex]420[/latex] calories
- Small fries – [latex]230[/latex] calories
- [latex]\text{12-oz}[/latex] chocolate shake – [latex]580[/latex] calories
What was the total number of calories of Fred’s dinner?
Test scores
A students needs a total of [latex]400[/latex] points on five tests to pass a course. The student scored [latex]82,91,75,88,\text{and}70[/latex]. Did the student pass the course?
Elevators
The maximum weight capacity of an elevator is [latex]1150[/latex] pounds. Six men are in the elevator. Their weights are 210, 145, 183, 230, 159, and 164 pounds. Is the total weight below the elevators’ maximum capacity?
Writing Exercises
How confident do you feel about your knowledge of the addition facts? If you are not fully confident, what will you do to improve your skills?
How have you used models to help you learn the addition facts?
Subtracting Whole Numbers
Use Subtraction Notation
In the following exercises, translate from math notation to words.
- [latex]15 - 9[/latex]
Show Solution
- [latex]18 - 16[/latex]
- [latex]42 - 35[/latex]
Show Solution
- [latex]83 - 64[/latex]
- [latex]675 - 350[/latex]
Show Solution
- [latex]790 - 525[/latex]
Model Subtraction of Whole Numbers
In the following exercises, model the subtraction.
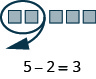
- [latex]5 - 2[/latex]
Show Solution
- [latex]8 - 4[/latex]
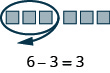
- [latex]6 - 3[/latex]
Show Solution
- [latex]7 - 5[/latex]
- [latex]18 - 5[/latex]
Show Solution
- [latex]19 - 8[/latex]
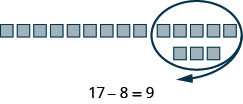
- [latex]17 - 8[/latex]
Show Solution
- [latex]17 - 9[/latex]
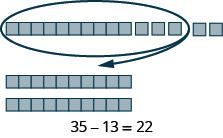
- [latex]35 - 13[/latex]
Show Solution
- [latex]32 - 11[/latex]
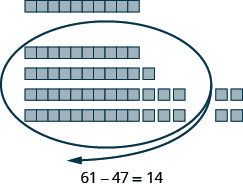
- [latex]61 - 47[/latex]
Show Solution
- [latex]55 - 36[/latex]
Subtract Whole Numbers
In the following exercises, subtract and then check by adding.
- [latex]9 - 4[/latex]
Show Solution
- [latex]9 - 3[/latex]
- [latex]8 - 0[/latex]
Show Solution
- [latex]2 - 0[/latex]
- [latex]38 - 16[/latex]
Show Solution
- [latex]45 - 21[/latex]
- [latex]85 - 52[/latex]
Show Solution
- [latex]99 - 47[/latex]
- [latex]493 - 370[/latex]
Show Solution
- [latex]268 - 106[/latex]
- [latex]5,946 - 4,625[/latex]
Show Solution
- [latex]7,775 - 3,251[/latex]
- [latex]75 - 47[/latex]
Show Solution
- [latex]63 - 59[/latex]
- [latex]461 - 239[/latex]
Show Solution
- [latex]486 - 257[/latex]
- [latex]525 - 179[/latex]
Show Solution
- [latex]542 - 288[/latex]
- [latex]6,318 - 2,799[/latex]
Show Solution
- [latex]8,153 - 3,978[/latex]
- [latex]2,150 - 964[/latex]
Show Solution
- [latex]4,245 - 899[/latex]
- [latex]43,650 - 8,982[/latex]
Show Solution
- [latex]35,162 - 7,885[/latex]
Translate Word Phrases to Algebraic Expressions
In the following exercises, translate and simplify.
- The difference of [latex]10[/latex] and [latex]3[/latex]
Show Solution
- The difference of [latex]12[/latex] and [latex]8[/latex]
- The difference of [latex]15[/latex] and [latex]4[/latex]
Show Solution
- The difference of [latex]18[/latex] and [latex]7[/latex]
- Subtract [latex]6[/latex] from [latex]9[/latex]
Show Solution
- Subtract [latex]8[/latex] from [latex]9[/latex]
- Subtract [latex]28[/latex] from [latex]75[/latex]
Show Solution
- Subtract [latex]59[/latex] from [latex]81[/latex]
- [latex]45[/latex] decreased by [latex]20[/latex]
Show Solution
- [latex]37[/latex] decreased by [latex]24[/latex]
- [latex]92[/latex] decreased by [latex]67[/latex]
Show Solution
- [latex]75[/latex] decreased by [latex]49[/latex]
- [latex]12[/latex] less than [latex]16[/latex]
Show Solution
- [latex]15[/latex] less than [latex]19[/latex]
- [latex]38[/latex] less than [latex]61[/latex]
Show Solution
- [latex]47[/latex] less than [latex]62[/latex]
Mixed Practice
In the following exercises, simplify.
- [latex]76 - 47[/latex]
Show Solution
- [latex]91 - 53[/latex]
- [latex]256 - 184[/latex]
Show Solution
- [latex]305 - 262[/latex]
- [latex]719+341[/latex]
Show Solution
- [latex]647+528[/latex]
- [latex]2,015 - 1,993[/latex]
Show Solution
- [latex]2,020 - 1,984[/latex]
In the following exercises, translate and simplify.
- Seventy more than thirty-five
Show Solution
- Sixty more than ninety-three
- [latex]13[/latex] less than [latex]41[/latex]
Show Solution
- [latex]28[/latex] less than [latex]36[/latex]
- The difference of [latex]100[/latex] and [latex]76[/latex]
Show Solution
- The difference of [latex]1,000[/latex] and [latex]945[/latex]
Subtract Whole Numbers in Applications
In the following exercises, solve.
Temperature
The high temperature on June 2 in Las Vegas was 80 degrees and the low temperature was 63 degrees. What was the difference between the high and low temperatures?
Temperature
The high temperature on June 1 in Phoenix was 97 degrees and the low was 73 degrees. What was the difference between the high and low temperatures?
Class size
Olivia’s third grade class has [latex]35[/latex] children. Last year, her second grade class had [latex]22[/latex] children. What is the difference between the number of children in Olivia’s third grade class and her second grade class?
Class size
There are [latex]82[/latex] students in the school band and [latex]46[/latex] in the school orchestra. What is the difference between the number of students in the band and the orchestra?
Shopping
A mountain bike is on sale for [latex]\$399[/latex]. Its regular price is [latex]\$650[/latex]. What is the difference between the regular price and the sale price?
Shopping
A mattress set is on sale for [latex]\$755[/latex]. Its regular price is [latex]\$1,600[/latex]. What is the difference between the regular price and the sale price?
Savings
John wants to buy a laptop that costs [latex]\$840[/latex]. He has [latex]\$685[/latex] in his savings account. How much more does he need to save in order to buy the laptop?
Banking
Mason had [latex]\$1,125[/latex] in his checking account. He spent [latex]\$892[/latex]. How much money does he have left?
Everyday Math
Road trip
Noah was driving from Philadelphia to Cincinnati, a distance of [latex]502[/latex] miles. He drove [latex]115[/latex] miles, stopped for gas, and then drove another [latex]230[/latex] miles before lunch. How many more miles did he have to travel?
Test Scores
Sara needs [latex]350[/latex] points to pass her course. She scored [latex]75,50,70,\text{and}80[/latex] on her first four tests. How many more points does Sara need to pass the course?
Writing Exercises
Explain how subtraction and addition are related.
How does knowing addition facts help you to subtract numbers?
Multiplying Whole Numbers
Use Multiplication Notation
In the following exercises, translate from math notation to words.
- [latex]4\times 7[/latex]
Show Solution
- [latex]8\times 6[/latex]
- [latex]5\cdot 12[/latex]
Show Solution
- [latex]3\cdot 9[/latex]
- [latex]\left(10\right)\left(25\right)[/latex]
Show Solution
- [latex]\left(20\right)\left(15\right)[/latex]
- [latex]42\left(33\right)[/latex]
Show Solution
- [latex]39\left(64\right)[/latex]
Model Multiplication of Whole Numbers
In the following exercises, model the multiplication.
- [latex]3\times 6[/latex]
Show Solution
- [latex]4\times 5[/latex]
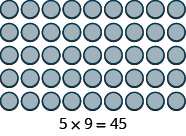
- [latex]5\times 9[/latex]
Show Solution
- [latex]3\times 9[/latex]
Multiply Whole Numbers
In the following exercises, fill in the missing values in each chart.
Exercise 1
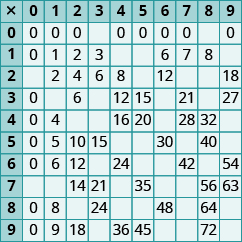
Exercise 2
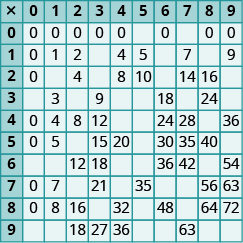
Exercise 3
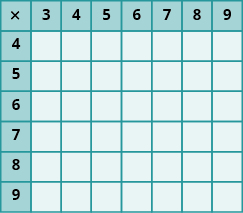
Exercise 4
Exercise 5
Exercise 6
Exercise 7
Exercise 8
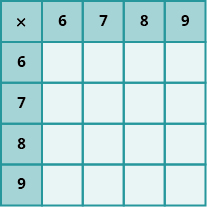
Multiply Whole Numbers
In the following exercises, multiply.
- [latex]0\cdot 15[/latex]
Show Solution
- [latex]0\cdot 41[/latex]
- [latex]\left(99\right)0[/latex]
Show Solution
- [latex]\left(77\right)0[/latex]
- [latex]1\cdot 43[/latex]
Show Solution
- [latex]1\cdot 34[/latex]
- [latex]\left(28\right)1[/latex]
Show Solution
- [latex]\left(65\right)1[/latex]
- [latex]1\left(240,055\right)[/latex]
Show Solution
- [latex]1\left(189,206\right)[/latex]
- [latex]7\cdot 6[/latex]
Show Solution
- [latex]6\cdot 7[/latex]
Show Solution
- [latex]8\times 9[/latex]
- [latex]9\times 8[/latex]
- [latex]\left(79\right)\left(5\right)[/latex]
Show Solution
- [latex]\left(58\right)\left(4\right)[/latex]
- [latex]275\cdot 6[/latex]
Show Solution
- [latex]638\cdot 5[/latex]
- [latex]3,421\times 7[/latex]
Show Solution
- [latex]9,143\times 3[/latex]
- [latex]52\left(38\right)[/latex]
Show Solution
- [latex]37\left(45\right)[/latex]
- [latex]96\cdot 73[/latex]
Show Solution
- [latex]89\cdot 56[/latex]
- [latex]27\times 85[/latex]
Show Solution
- [latex]53\times 98[/latex]
- [latex]23\cdot 10[/latex]
Show Solution
- [latex]19\cdot 10[/latex]
- [latex]\left(100\right)\left(36\right)[/latex]
Show Solution
- [latex]\left(100\right)\left(25\right)[/latex]
- [latex]1,000\left(88\right)[/latex]
Show Solution
- [latex]1,000\left(46\right)[/latex]
- [latex]50\times 1,000,000[/latex]
Show Solution
- [latex]30\times 1,000,000[/latex]
- [latex]247\times 139[/latex]
Show Solution
- [latex]156\times 328[/latex]
- [latex]586\left(721\right)[/latex]
Show Solution
- [latex]472\left(855\right)[/latex]
- [latex]915\cdot 879[/latex]
Show Solution
- [latex]968\cdot 926[/latex]
- [latex]\left(104\right)\left(256\right)[/latex]
Show Solution
- [latex]\left(103\right)\left(497\right)[/latex]
- [latex]348\left(705\right)[/latex]
Show Solution
- [latex]485\left(602\right)[/latex]
- [latex]2,719\times 543[/latex]
Show Solution
- [latex]3,581\times 724[/latex]
Translate Word Phrases to Math Notation
In the following exercises, translate and simplify.
- the product of [latex]18[/latex] and [latex]33[/latex]
Show Solution
- the product of [latex]15[/latex] and [latex]22[/latex]
- fifty-one times sixty-seven
Show Solution
- forty-eight times seventy-one
- twice [latex]249[/latex]
Show Solution
- twice [latex]589[/latex]
- ten times three hundred seventy-five
Show Solution
- ten times two hundred fifty-five
Mixed Practice, Part I
In the following exercises, simplify.
- [latex]38\times 37[/latex]
Show Solution
- [latex]86\times 29[/latex]
- [latex]415 - 267[/latex]
Show Solution
- [latex]341 - 285[/latex]
- [latex]6,251+4,749[/latex]
Show Solution
- [latex]3,816+8,184[/latex]
- [latex]\left(56\right)\left(204\right)[/latex]
Show Solution
- [latex]\left(77\right)\left(801\right)[/latex]
- [latex]947\cdot 0[/latex]
Show Solution
- [latex]947+0[/latex]
- [latex]15,382+1[/latex]
Show Solution
- [latex]15,382\cdot 1[/latex]
Mixed Practice, Part II
In the following exercises, translate and simplify.
- the difference of 50 and 18
Show Solution
- the difference of 90 and 66
- twice 35
Show Solution
- twice 140
- 20 more than 980
Show Solution
- 65 more than 325
- the product of 12 and 875
Show Solution
- the product of 15 and 905
- subtract 74 from 89
Show Solution
- subtract 45 from 99
- the sum of 3,075 and 95
Show Solution
- the sum of 6,308 and 724
- 366 less than 814
Show Solution
- 388 less than 925
Multiply Whole Numbers in Applications
In the following exercises, solve.
Party supplies
Tim brought 9 six-packs of soda to a club party. How many cans of soda did Tim bring?
Sewing
Kanisha is making a quilt. She bought 6 cards of buttons. Each card had four buttons on it. How many buttons did Kanisha buy?
Field trip
Seven school busses let off their students in front of a museum in Washington, DC. Each school bus had 44 students. How many students were there?
Gardening
Kathryn bought 8 flats of impatiens for her flower bed. Each flat has 24 flowers. How many flowers did Kathryn buy?
Charity
Rey donated 15 twelve-packs of t-shirts to a homeless shelter. How many t-shirts did he donate?
School
There are 28 classrooms at Anna C. Scott elementary school. Each classroom has 26 student desks. What is the total number of student desks?
Recipe
Stephanie is making punch for a party. The recipe calls for twice as much fruit juice as club soda. If she uses 10 cups of club soda, how much fruit juice should she use?
Gardening
Hiroko is putting in a vegetable garden. He wants to have twice as many lettuce plants as tomato plants. If he buys 12 tomato plants, how many lettuce plants should he get?
Government
The United States Senate has twice as many senators as there are states in the United States. There are 50 states. How many senators are there in the United States Senate?
Recipe
Andrea is making potato salad for a buffet luncheon. The recipe says the number of servings of potato salad will be twice the number of pounds of potatoes. If she buys 30 pounds of potatoes, how many servings of potato salad will there be?
Painting
Jane is painting one wall of her living room. The wall is rectangular, 13 feet wide by 9 feet high. What is the area of the wall?
Home décor
Shawnte bought a rug for the hall of her apartment. The rug is 3 feet wide by 18 feet long. What is the area of the rug?
Room size
The meeting room in a senior center is rectangular, with length 42 feet and width 34 feet. What is the area of the meeting room?
Gardening
June has a vegetable garden in her yard. The garden is rectangular, with length 23 feet and width 28 feet. What is the area of the garden?
NCAA basketball
According to NCAA regulations, the dimensions of a rectangular basketball court must be 94 feet by 50 feet. What is the area of the basketball court?
NCAA football
According to NCAA regulations, the dimensions of a rectangular football field must be 360 feet by 160 feet. What is the area of the football field?
Everyday Math
Stock market
Javier owns 300 shares of stock in one company. On Tuesday, the stock price rose [latex]\$12[/latex] per share. How much money did Javier’s portfolio gain?
Salary
Carlton got a [latex]\$200[/latex] raise in each paycheck. He gets paid 24 times a year. How much higher is his new annual salary?
Writing Exercises
How confident do you feel about your knowledge of the multiplication facts? If you are not fully confident, what will you do to improve your skills?
How have you used models to help you learn the multiplication facts?
Dividing Whole Numbers
Use Division Notation
In the following exercises, translate from math notation to words.
- [latex]54\div 9[/latex]
Show Solution
- [latex]\frac{56}{7}[/latex]
- [latex]\frac{32}{8}[/latex]
Show Solution
- [latex]6\overline{)42}[/latex]
- [latex]48\div 6[/latex]
Show Solution
- [latex]\frac{63}{9}[/latex]
- [latex]7\overline{)63}[/latex]
Show Solution
- [latex]72\div 8[/latex]
Model Division of Whole Numbers
In the following exercises, model the division.
- [latex]15\div 5[/latex]
Show Solution
- [latex]10\div 5[/latex]
- [latex]\frac{14}{7}[/latex]
Show Solution
- [latex]\frac{18}{6}[/latex]
- [latex]4\overline{)20}[/latex]
Show Solution
- [latex]3\overline{)15}[/latex]
- [latex]24\div 6[/latex]
Show Solution
- [latex]16\div 4[/latex]
Divide Whole Numbers
In the following exercises, divide. Then check by multiplying.
- [latex]18\div 2[/latex]
Show Solution
- [latex]14\div 2[/latex]
- [latex]\frac{27}{3}[/latex]
Show Solution
- [latex]\frac{30}{3}[/latex]
- [latex]4\overline{)28}[/latex]
Show Solution
- [latex]4\overline{)36}[/latex]
- [latex]\frac{45}{5}[/latex]
Show Solution
- [latex]\frac{35}{5}[/latex]
- [latex]72/8[/latex]
Show Solution
- [latex]8\overline{)64}[/latex]
- [latex]\frac{35}{7}[/latex]
Show Solution
- [latex]42\div 7[/latex]
- [latex]15\overline{)15}[/latex]
Show Solution
- [latex]12\overline{)12}[/latex]
- [latex]43\div 43[/latex]
Show Solution
- [latex]37\div 37[/latex]
- [latex]\frac{23}{1}[/latex]
Show Solution
- [latex]\frac{29}{1}[/latex]
- [latex]19\div 1[/latex]
Show Solution
- [latex]17\div 1[/latex]
- [latex]0\div 4[/latex]
Show Solution
- [latex]0\div 8[/latex]
- [latex]\frac{5}{0}[/latex]
Show Solution
- [latex]\frac{9}{0}[/latex]
- [latex]\frac{26}{0}[/latex]
Show Solution
- [latex]\frac{32}{0}[/latex]
- [latex]12\overline{)0}[/latex]
Show Solution
- [latex]16\overline{)0}[/latex]
- [latex]72\div 3[/latex]
Show Solution
- [latex]57\div 3[/latex]
- [latex]\frac{96}{8}[/latex]
Show Solution
- [latex]\frac{78}{6}[/latex]
- [latex]5\overline{)465}[/latex]
Show Solution
- [latex]4\overline{)528}[/latex]
- [latex]924\div 7[/latex]
Show Solution
- [latex]861\div 7[/latex]
- [latex]\frac{5,226}{6}[/latex]
Show Solution
- [latex]\frac{3,776}{8}[/latex]
- [latex]4\overline{)31,324}[/latex]
Show Solution
- [latex]5\overline{)46,855}[/latex]
- [latex]7,209\div 3[/latex]
Show Solution
- [latex]4,806\div 3[/latex]
- [latex]5,406\div 6[/latex]
Show Solution
- [latex]3,208\div 4[/latex]
- [latex]4\overline{)2,816}[/latex]
Show Solution
- [latex]6\overline{)3,624}[/latex]
- [latex]\frac{91,881}{9}[/latex]
Show Solution
- [latex]\frac{83,256}{8}[/latex]
- [latex]2,470\div 7[/latex]
Show Solution
- [latex]3,741\div 7[/latex]
- [latex]8\overline{)55,305}[/latex]
Show Solution
- [latex]9\overline{)51,492}[/latex]
- [latex]\frac{431,174}{5}[/latex]
Show Solution
- [latex]\frac{297,277}{4}[/latex]
- [latex]130,016\div 3[/latex]
Show Solution
- [latex]105,609\div 2[/latex]
- [latex]15\overline{)5,735}[/latex]
Show Solution
- [latex]\frac{4,933}{21}[/latex]
- [latex]56,883\div 67[/latex]
Show Solution
- [latex]43,725/75[/latex]
- [latex]\frac{30,144}{314}[/latex]
Show Solution
- [latex]26,145\div 415[/latex]
- [latex]273\overline{)542,195}[/latex]
Show Solution
- [latex]816,243\div 462[/latex]
Mixed Practice
In the following exercises, simplify.
- [latex]15\left(204\right)[/latex]
Show Solution
- [latex]74\cdot 391[/latex]
- [latex]256 - 184[/latex]
Show Solution
- [latex]305 - 262[/latex]
- [latex]719+341[/latex]
Show Solution
- [latex]647+528[/latex]
- [latex]25\overline{)875}[/latex]
Show Solution
- [latex]1104\div 23[/latex]
Translate Word Phrases to Algebraic Expressions
In the following exercises, translate and simplify.
- the quotient of [latex]45[/latex] and [latex]15[/latex]
Show Solution
- the quotient of [latex]64[/latex] and [latex]16[/latex]
- the quotient of [latex]288[/latex] and [latex]24[/latex]
Show Solution
- the quotient of [latex]256[/latex] and [latex]32[/latex]
Divide Whole Numbers in Applications
In the following exercises, solve.
Trail mix
Ric bought [latex]64[/latex] ounces of trail mix. He wants to divide it into small bags, with [latex]2[/latex] ounces of trail mix in each bag. How many bags can Ric fill?
Crackers
Evie bought a [latex]42[/latex] ounce box of crackers. She wants to divide it into bags with [latex]3[/latex] ounces of crackers in each bag. How many bags can Evie fill?
Astronomy class
There are [latex]125[/latex] students in an astronomy class. The professor assigns them into groups of [latex]5[/latex]. How many groups of students are there?
Flower shop
Melissa’s flower shop got a shipment of [latex]152[/latex] roses. She wants to make bouquets of [latex]8[/latex] roses each. How many bouquets can Melissa make?
Baking
One roll of plastic wrap is [latex]48[/latex] feet long. Marta uses [latex]3[/latex] feet of plastic wrap to wrap each cake she bakes. How many cakes can she wrap from one roll?
Dental floss
One package of dental floss is [latex]54[/latex] feet long. Brian uses [latex]2[/latex] feet of dental floss every day. How many days will one package of dental floss last Brian?
Everyday Math
Contact lenses
Jenna puts in a new pair of contact lenses every [latex]14[/latex] days. How many pairs of contact lenses does she need for [latex]365[/latex] days?
Cat food
One bag of cat food feeds Lara’s cat for [latex]25[/latex] days. How many bags of cat food does Lara need for [latex]365[/latex] days?
Writing Exercises
Explain how you use the multiplication facts to help with division.
Oswaldo divided [latex]300[/latex] by [latex]8[/latex] and said his answer was [latex]37[/latex] with a remainder of [latex]4[/latex]. How can you check to make sure he is correct?
Mixed Practice (Applications)
In the following exercises, solve.
Miles per gallon
Susana’s hybrid car gets [latex]45[/latex] miles per gallon. Her son’s truck gets [latex]17[/latex] miles per gallon. What is the difference in miles per gallon between Susana’s car and her son’s truck?
Distance
Mayra lives [latex]53[/latex] miles from her mother’s house and [latex]71[/latex] miles from her mother-in-law’s house. How much farther is Mayra from her mother-in-law’s house than from her mother’s house?
Field trip
The [latex]45[/latex] students in a Geology class will go on a field trip, using the college’s vans. Each van can hold [latex]9[/latex] students. How many vans will they need for the field trip?
Potting soil
Aki bought a [latex]128[/latex] ounce bag of potting soil. How many [latex]4[/latex] ounce pots can he fill from the bag?
Hiking
Bill hiked [latex]8[/latex] miles on the first day of his backpacking trip, [latex]14[/latex] miles the second day, [latex]11[/latex] miles the third day, and [latex]17[/latex] miles the fourth day. What is the total number of miles Bill hiked?
Reading
Last night Emily read [latex]6[/latex] pages in her Business textbook, [latex]26[/latex] pages in her History text, [latex]15[/latex] pages in her Psychology text, and [latex]9[/latex] pages in her math text. What is the total number of pages Emily read?
Patients
LaVonne treats [latex]12[/latex] patients each day in her dental office. Last week she worked [latex]4[/latex] days. How many patients did she treat last week?
Scouts
There are [latex]14[/latex] boys in Dave’s scout troop. At summer camp, each boy earned [latex]5[/latex] merit badges. What was the total number of merit badges earned by Dave’s scout troop at summer camp?
Chapter Review Exercises
Introduction to Whole Numbers
Identify Counting Numbers and Whole Numbers
In the following exercises, determine which of the following are (a) counting numbers (b) whole numbers.
- [latex]0,2,99[/latex]
Show Solution
- [latex]0,3,25[/latex]
- [latex]0,4,90[/latex]
Show Solution
- [latex]0,1,75[/latex]
Model Whole Numbers
In the following exercises, model each number using [latex]\text{base - 10}[/latex] blocks and then show its value using place value notation.
- 258
Show Solution
- 104
Identify the Place Value of a Digit
In the following exercises, find the place value of the given digits.
[latex]472,981[/latex]
- [latex]8[/latex]
- [latex]4[/latex]
- [latex]1[/latex]
- [latex]7[/latex]
- [latex]2[/latex]
[latex]12,403,295[/latex]
- [latex]4[/latex]
- [latex]0[/latex]
- [latex]1[/latex]
- [latex]9[/latex]
- [latex]3[/latex]
Use Place Value to Name Whole Numbers
In the following exercises, name each number in words.
- [latex]5,280[/latex]
Show Solution
- [latex]204,614[/latex]
- [latex]5,012,582[/latex]
Show Solution
- [latex]31,640,976[/latex]
Use Place Value to Write Whole Numbers
In the following exercises, write as a whole number using digits.
- six hundred two
- fifteen thousand, two hundred fifty-three
Show Solution
- three hundred forty million, nine hundred twelve thousand, sixty-one
Show Solution
- two billion, four hundred ninety-two million, seven hundred eleven thousand, two
Round Whole Numbers
In the following exercises, round to the nearest ten.
- [latex]412[/latex]
Show Solution
- [latex]648[/latex]
- [latex]3,556[/latex]
Show Solution
- [latex]2,734[/latex]
In the following exercises, round to the nearest hundred.
- [latex]38,975[/latex]
Show Solution
- [latex]26,849[/latex]
- [latex]81,486[/latex]
Show Solution
- [latex]75,992[/latex]
Add Whole Numbers
Use Addition Notation
In the following exercises, translate the following from math notation to words.
- [latex]4+3[/latex]
Show Solution
- [latex]25+18[/latex]
- [latex]571+629[/latex]
Show Solution
- [latex]10,085+3,492[/latex]
Model Addition of Whole Numbers
In the following exercises, model the addition.
- [latex]6+7[/latex]
Show Solution
- [latex]38+14[/latex]
Add Whole Numbers
In the following exercises, fill in the missing values in each chart.
Exercise 1
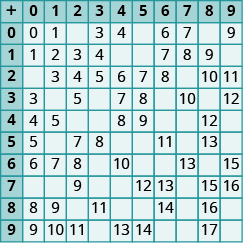
Exercise 2
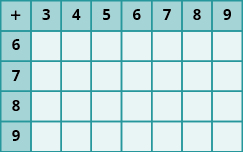
In the following exercises, add.
- [latex]0+19[/latex]
Show Solution
- [latex]19+0[/latex]
Show Solution
- [latex]0+480[/latex]
- [latex]480+0[/latex]
- [latex]7+6[/latex]
Show Solution
- [latex]6+7[/latex]
Show Solution
- [latex]23+18[/latex]
- [latex]18+23[/latex]
- [latex]44+35[/latex]
Show Solution
- [latex]63+29[/latex]
- [latex]96+58[/latex]
Show Solution
- [latex]375+591[/latex]
- [latex]7,281+12,546[/latex]
Show Solution
- [latex]5,280+16,324+9,731[/latex]
Translate Word Phrases to Math Notation
In the following exercises, translate each phrase into math notation and then simplify.
- the sum of [latex]30[/latex] and [latex]12[/latex]
Show Solution
- [latex]11[/latex] increased by [latex]8[/latex]
- [latex]25[/latex] more than [latex]39[/latex]
Show Solution
- total of [latex]15[/latex] and [latex]50[/latex]
Add Whole Numbers in Applications
In the following exercises, solve.
Shopping for an interview
Nathan bought a new shirt, tie, and slacks to wear to a job interview. The shirt cost [latex]\$24[/latex], the tie cost [latex]\$14[/latex], and the slacks cost [latex]\$38[/latex]. What was Nathan’s total cost?
Running
Jackson ran [latex]4[/latex] miles on Monday, [latex]12[/latex] miles on Tuesday, [latex]1[/latex] mile on Wednesday, [latex]8[/latex] miles on Thursday, and [latex]5[/latex] miles on Friday. What was the total number of miles Jackson ran?
Add Whole Numbers in Applications
In the following exercises, find the perimeter of each figure.
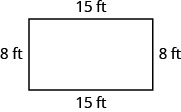
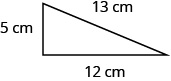
Subtract Whole Numbers
Use Subtraction Notation
In the following exercises, translate the following from math notation to words.
- [latex]14 - 5[/latex]
Show Solution
- [latex]40 - 15[/latex]
- [latex]351 - 249[/latex]
Show Solution
- [latex]5,724 - 2,918[/latex]
Model Subtraction of Whole Numbers
In the following exercises, model the subtraction.
- [latex]18 - 4[/latex]
Show Solution
- [latex]41 - 29[/latex]
Subtract Whole Numbers
In the following exercises, subtract and then check by adding.
- [latex]8 - 5[/latex]
Show Solution
- [latex]12 - 7[/latex]
- [latex]23 - 9[/latex]
Show Solution
- [latex]46 - 21[/latex]
- [latex]82 - 59[/latex]
Show Solution
- [latex]110 - 87[/latex]
- [latex]539 - 217[/latex]
Show Solution
- [latex]415 - 296[/latex]
- [latex]1,020 - 640[/latex]
Show Solution
- [latex]8,355 - 3,947[/latex]
- [latex]10,000 - 15[/latex]
Show Solution
- [latex]54,925 - 35,647[/latex]
Translate Word Phrases to Math Notation
In the following exercises, translate and simplify.
- the difference of nineteen and thirteen
Show Solution
- subtract sixty-five from one hundred
- seventy-four decreased by eight
Show Solution
- twenty-three less than forty-one
Subtract Whole Numbers in Applications
In the following exercises, solve.
Temperature
The high temperature in Peoria one day was [latex]86[/latex] degrees Fahrenheit and the low temperature was [latex]28[/latex] degrees Fahrenheit. What was the difference between the high and low temperatures?
Savings
Lynn wants to go on a cruise that costs [latex]\$2,485[/latex]. She has [latex]\$948[/latex] in her vacation savings account. How much more does she need to save in order to pay for the cruise?
Multiply Whole Numbers
Use Multiplication Notation
In the following exercises, translate from math notation to words.
- [latex]8\times 5[/latex]
Show Solution
- [latex]6\cdot 14[/latex]
- [latex]\left(10\right)\left(95\right)[/latex]
Show Solution
- [latex]54\left(72\right)[/latex]
Model Multiplication of Whole Numbers
In the following exercises, model the multiplication.
- [latex]2\times 4[/latex]
Show Solution
- [latex]3\times 8[/latex]
Multiply Whole Numbers
In the following exercises, fill in the missing values in each chart.
Exercises 1
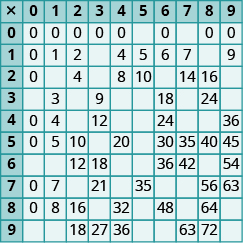
Exercises 2
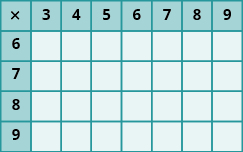
Multiply Whole Numbers
In the following exercises, multiply.
- [latex]0\cdot 14[/latex]
Show Solution
- [latex]\left(256\right)0[/latex]
- [latex]1\cdot 99[/latex]
Show Solution
- [latex]\left(4,789\right)1[/latex]
- [latex]7\cdot 4[/latex]
Show Solution
- [latex]4\cdot 7[/latex]
Show Solution
- [latex]\left(25\right)\left(6\right)[/latex]
- [latex]9,261\times 3[/latex]
Show Solution
- [latex]48\cdot 76[/latex]
- [latex]64\cdot 10[/latex]
Show Solution
- [latex]1,000\left(22\right)[/latex]
- [latex]162\times 493[/latex]
Show Solution
- [latex]\left(601\right)\left(943\right)[/latex]
- [latex]3,624\times 517[/latex]
Show Solution
- [latex]10,538\cdot 22[/latex]
Translate Word Phrases to Math Notation
In the following exercises, translate and simplify.
- the product of [latex]15[/latex] and [latex]28[/latex]
Show Solution
- ninety-four times thirty-three
- twice [latex]575[/latex]
Show Solution
- ten times two hundred sixty-four
Multiply Whole Numbers in Applications
In the following exercises, solve.
Gardening
Geniece bought [latex]8[/latex] packs of marigolds to plant in her yard. Each pack has [latex]6[/latex] flowers. How many marigolds did Geniece buy?
Cooking
Ratika is making rice for a dinner party. The number of cups of water is twice the number of cups of rice. If Ratika plans to use [latex]4[/latex] cups of rice, how many cups of water does she need?
Multiplex
There are twelve theaters at the multiplex and each theater has [latex]150[/latex] seats. What is the total number of seats at the multiplex?
Roofing
Lewis needs to put new shingles on his roof. The roof is a rectangle, [latex]30[/latex] feet by [latex]24[/latex] feet. What is the area of the roof?
Divide Whole Numbers
Use Division Notation
Translate from math notation to words.
- [latex]54\div 9[/latex]
Show Solution
- [latex]42/7[/latex]
- [latex]\frac{72}{8}[/latex]
Show Solution
- [latex]6\overline{)48}[/latex]
Model Division of Whole Numbers
In the following exercises, model.
- [latex]8\div 2[/latex]
Show Solution
- [latex]3\overline{)12}[/latex]
Divide Whole Numbers
In the following exercises, divide. Then check by multiplying.
- [latex]14\div 2[/latex]
Show Solution
- [latex]\frac{32}{8}[/latex]
- [latex]52\div 4[/latex]
Show Solution
- [latex]26\overline{)26}[/latex]
- [latex]\frac{97}{1}[/latex]
Show Solution
- [latex]0\div 52[/latex]
- [latex]100\div 0[/latex]
Show Solution
- [latex]\frac{355}{5}[/latex]
- [latex]3828\div 6[/latex]
Show Solution
- [latex]31\overline{)1,519}[/latex]
- [latex]\frac{7505}{25}[/latex]
Show Solution
- [latex]5,166\div 42[/latex]
Translate Word Phrases to Math Notation
In the following exercises, translate and simplify.
- the quotient of [latex]64[/latex] and [latex]16[/latex]
Show Solution
- the quotient of [latex]572[/latex] and [latex]52[/latex]
Divide Whole Numbers in Applications
In the following exercises, solve.
Ribbon
One spool of ribbon is [latex]27[/latex] feet. Lizbeth uses [latex]3[/latex] feet of ribbon for each gift basket that she wraps. How many gift baskets can Lizbeth wrap from one spool of ribbon?
Juice
One carton of fruit juice is [latex]128[/latex] ounces. How many [latex]4[/latex] ounce cups can Shayla fill from one carton of juice?
Chapter Practice Test
Determine which of the following numbers are a) counting numbers and b) whole numbers.
- [latex]0,4,87[/latex]
Show Solution
Find the place value of the given digits in the number [latex]549,362[/latex].
- [latex]9[/latex]
- [latex]6[/latex]
- [latex]2[/latex]
- [latex]5[/latex]
Write each number as a whole number using digits.
- six hundred thirteen
Show Solution
- fifty-five thousand two hundred eight
Show Solution
Round [latex]25,849[/latex] to the nearest hundred.
Simplify.
- [latex]45+23[/latex]
Show Solution
- [latex]65 - 42[/latex]
- [latex]85\div 5[/latex]
Show Solution
- [latex]1,000\times 8[/latex]
- [latex]90 - 58[/latex]
Show Solution
- [latex]73+89[/latex]
- [latex]\left(0\right)\left(12,675\right)[/latex]
Show Solution
- [latex]634+255[/latex]
- [latex]\frac{0}{9}[/latex]
Show Solution
- [latex]8\overline{)128}[/latex]
- [latex]145 - 79[/latex]
Show Solution
- [latex]299+836[/latex]
- [latex]7\cdot 475[/latex]
Show Solution
- [latex]8,528+704[/latex]
- [latex]35\left(14\right)[/latex]
Show Solution
- [latex]\frac{26}{0}[/latex]
- [latex]733 - 291[/latex]
Show Solution
- [latex]4,916 - 1,538[/latex]
- [latex]495\div 45[/latex]
Show Solution
- [latex]52\times 983[/latex]
Translate each phrase to math notation and then simplify.
- The sum of [latex]16[/latex] and [latex]58[/latex]
Show Solution
- The product of [latex]9[/latex] and [latex]15[/latex]
- The difference of [latex]32[/latex] and [latex]18[/latex]
Show Solution
- The quotient of [latex]63[/latex] and [latex]21[/latex]
- Twice [latex]524[/latex]
Show Solution
- [latex]29[/latex] more than [latex]32[/latex]
- [latex]50[/latex] less than [latex]300[/latex]
Show Solution
In the following exercises, solve.
- LaVelle buys a jumbo bag of [latex]84[/latex] candies to make favor bags for her son’s party. If she wants to make [latex]12[/latex] bags, how many candies should she put in each bag?
- Last month, Stan’s take-home pay was [latex]\$3,816[/latex] and his expenses were [latex]\$3,472[/latex]. How much of his take-home pay did Stan have left after he paid his expenses?
Show Solution
- Each class at Greenville School has [latex]22[/latex] children enrolled. The school has [latex]24[/latex] classes. How many children are enrolled at Greenville School?
- Clayton walked [latex]12[/latex] blocks to his mother’s house, [latex]6[/latex] blocks to the gym, and [latex]9[/latex] blocks to the grocery store before walking the last [latex]3[/latex] blocks home. What was the total number of blocks that Clayton walked?
Show Solution
Candela Citations
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757