Applications of Systems of Linear Inequalities

Learning Outcomes

Interpret graphs and solutions to systems of linear inequalities

In our first example we will show how to write and graph a system of linear inequalities that models the amount of sales needed to obtain a specific amount of money.

Example

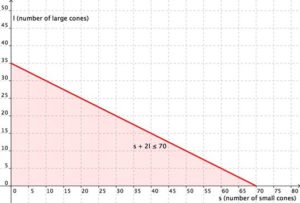
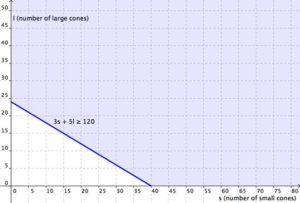
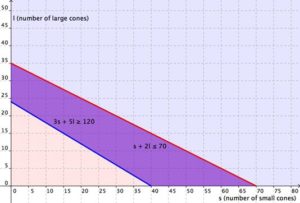
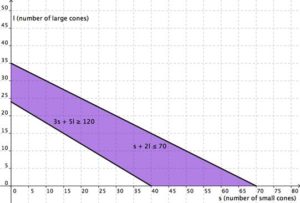
Cathy is selling ice cream cones at a school fundraiser. She is selling two sizes: small (which has [latex]1[/latex] scoop) and large (which has [latex]2[/latex] scoops). She knows that she can get a maximum of [latex]70[/latex] scoops of ice cream out of her supply. She charges [latex]$3[/latex] for a small cone and [latex]$5[/latex] for a large cone.

Cathy wants to earn at least [latex]$120[/latex] to give back to the school. Write and graph a system of inequalities that models this situation.

Show Solution

In a previous example for finding a solution to a system of linear equations, we introduced a manufacturer’s cost and revenue equations:

Cost: [latex]y=0.85x+35,000[/latex]

Revenue: [latex]y=1.55x[/latex]

[latex]x\ge0,y\ge0[/latex]

The cost equation is shown in blue in the graph below, and the revenue equation is graphed in orange. The point at which the two lines intersect is called the break-even point. We learned that this is the solution to the system of linear equations that cause the cost and revenue equations to equal each other. Note how the lines shown only represent where [latex]x\ge0, y\ge0[/latex]. It is easy to forget to include this part in the graph.

The shaded region to the right of the break-even point represents quantities where the company makes a profit. The region to the left represents quantities where the company suffers a loss.

In the next example, you will see how the information you learned about systems of linear inequalities can be applied to answering questions about cost and revenue.

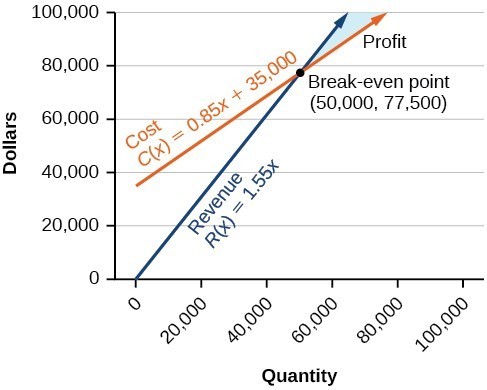
A graph showing money in dollars on the y axis and quantity on the x axis. A line representing cost and a line representing revenue cross at the break-even point of fifty thousand, seventy-seven thousand five hundred. The cost line's equation is C(x)=0.85x+35,000. The revenue line's equation is R(x)=1.55x. The shaded space between the two lines to the right of the break-even point is labeled profit.

Note how the blue shaded region between the cost and revenue equations is labeled profit. This is the “sweet spot” that the company wants to achieve where they produce enough bike frames at a minimal enough cost to make money. They do not want more money going out than coming in!

Example

Define the profit region for the bike manufacturing business using inequalities, given the system of linear equations:

Cost: [latex]y=0.85x+35,000[/latex]

Revenue: [latex]y=1.55x[/latex]

[latex]x\ge0, y\ge0[/latex]

Show Solution

Read and Understand: We know that, graphically, solutions to linear inequalities are entire regions, and we learned how to graph systems of linear inequalities earlier in this module. Based on the graph below and the equations that define cost and revenue, we can use inequalities to define the region where the skateboard manufacturer will make a profit. Again, note how only the region for [latex]x\ge0, y\ge0[/latex] is included.

A graph of the functions y equals 1.55 x and y equals 0.45 x plus 35000. The x and y axes span from 0 to 10. The graphs intersect at the labeled point (50000, 77500), and the area between the graphs to the right of the point of intersection is shaded blue.

Start with the revenue equation. We know that the break-even point is at [latex](50,000, 77,500)[/latex], and the profit region is the blue area. If we choose a point in the region and test it like we did for finding solution regions for inequalities, we will know which kind of inequality sign to use.

Test the point [latex]\left(65000,100000\right)[/latex] in both equations to determine which inequality sign to use.

Cost:

[latex]\begin{array}{l}y=0.85x+{35,000}\\{100,000}\text{ ? }0.85\left(65,000\right)+35,000\\100,000\text{ ? }90,250\end{array}[/latex]

We need to use > because [latex]100,000[/latex] is greater than [latex]90,250[/latex]

The cost inequality that will ensure the company makes profit, not just break-even, is [latex]y>0.85x+35,000[/latex]

Now test the point in the revenue equation:

Revenue:

[latex]\begin{array}{l}y=1.55x\\100,000\text{ ? }1.55\left(65,000\right)\\100,000\text{ ? }100,750\end{array}[/latex]

We need to use < because [latex]100,000[/latex] is less than [latex]100,750[/latex]

The revenue inequality that will ensure the company makes profit, not just break-even, is [latex]y<1.55x[/latex]

The system of inequalities that defines the profit region for the bike manufacturer is:

[latex]\begin{array}{l}y>0.85x+35,000\\y<1.55x\end{array}[/latex]

Answer

The cost to produce [latex]50,000[/latex] units is [latex]$77,500[/latex], and the revenue from the sales of [latex]50,000[/latex] units is also [latex]$77,500[/latex]. To make a profit, the business must produce and sell more than [latex]50,000[/latex] units. The system of linear inequalities that represents the number of units that the company must produce in order to earn a profit is:

[latex]\begin{array}{l}y>0.85x+35,000\\y<1.55x\end{array}[/latex]

In the following video, you will see an example of how to find the break-even point for a small sno-cone business.

Below is one more video example about solving an application using a system of linear inequalities.

We have seen that systems of linear equations and inequalities can help to define market behaviors that are very helpful to businesses. The intersection of cost and revenue equations gives the break-even point and also helps define the region where a company will make a profit.

Contribute!

Did you have an idea for improving this content? We’d love your input.

Improve this page Learn More

Module 16: Linear Systems