Graphing Solutions to Systems of Linear Inequalities
Learning Outcomes
Graph systems of linear inequalities
Graph a System of Two Inequalities
Remember from the module on graphing that the graph of a single linear inequality splits the coordinate plane into two regions. On one side lie all the solutions to the inequality. On the other side, there are no solutions. Consider the graph of the inequality [latex]y<2x+5[/latex].
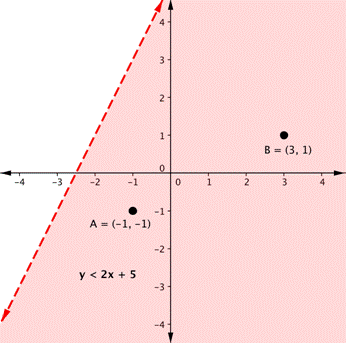
The dashed line is [latex]y=2x+5[/latex]. Every ordered pair in the shaded area below the line is a solution to [latex]y<2x+5[/latex], as all of the points below the line will make the inequality true. If you doubt that, try substituting the x and y coordinates of Points A and B into the inequality; you will see that they work. So, the shaded area shows all of the solutions for this inequality.
The boundary line divides the coordinate plane in half. In this case, it is shown as a dashed line as the points on the line do not satisfy the inequality. If the inequality had been [latex]y\leq2x+5[/latex], then the boundary line would have been solid.
Now graph another inequality: [latex]y>−x[/latex]. You can check a couple of points to determine which side of the boundary line to shade. Checking points M and N yield true statements. So, we shade the area above the line. The line is dashed as points on the line are not true.
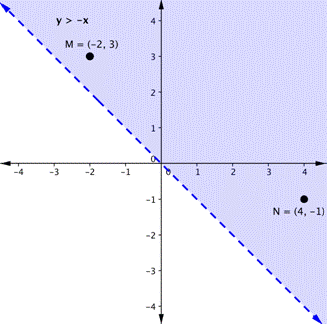
To create a system of inequalities, you need to graph two or more inequalities together. Let us use [latex]y<2x+5[/latex] and [latex]y>−x[/latex] since we have already graphed each of them.
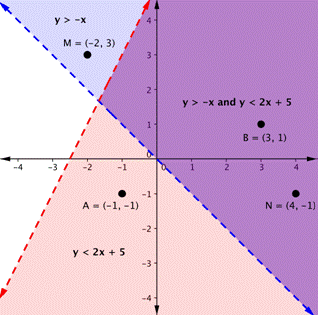
The purple area shows where the solutions of the two inequalities overlap. This area is the solution to the system of inequalities. Any point within this purple region will be true for both [latex]y>−x[/latex] and [latex]y<2x+5[/latex].
As shown above, finding the solutions of a system of inequalities can be done by graphing each inequality and identifying the region they share. The general steps are outlined below:
Graph each inequality as a line and determine whether it will be solid or dashed
Determine which side of each boundary line represents solutions to the inequality by testing a point on each side
Shade the region that represents solutions for both inequalities
We will continue to practice graphing the solution region for systems of linear inequalities. We will also graph the solutions to a system that includes a compound inequality.
Example
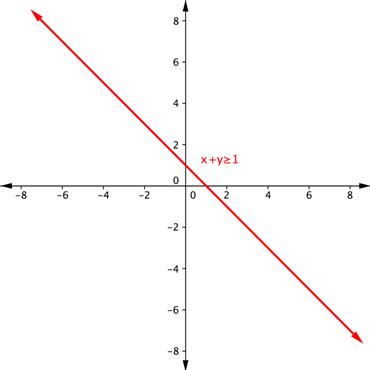
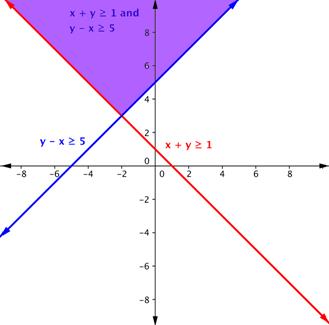
Shade the region of the graph that represents solutions for both inequalities. [latex]x+y\geq1[/latex] and [latex]y–x\geq5[/latex].
Show Solution
Graph one inequality. First graph the boundary line using a table of values, intercepts, or any other method you prefer. The boundary line for [latex]x+y\geq1[/latex] is [latex]x+y=1[/latex], or [latex]y=−x+1[/latex]. Since the equal sign is included with the greater than sign, the boundary line is solid.
Find an ordered pair on either side of the boundary line. Insert the x and y-values into the inequality [latex]x+y\geq1[/latex] and see which ordered pair results in a true statement.
Since [latex](4, 1)[/latex] results in a true statement, the region that includes [latex](4, 1)[/latex] should be shaded.
Do the same with the second inequality. Graph the boundary line, then test points to find which region is the solution to the inequality. In this case, the boundary line is [latex]y–x=5\left(\text{or }y=x+5\right)[/latex] and is solid. Test point [latex](−3, 0)[/latex] is not a solution of [latex]y–x\geq5[/latex] and test point [latex](0, 6)[/latex] is a solution.
The purple region in this graph shows the set of all solutions of the system.
The videos that follow show more examples of graphing the solution set of a system of linear inequalities.
The system in our next example includes a compound inequality. We will see that you can treat a compound inequality like two lines when you are graphing them.
Example
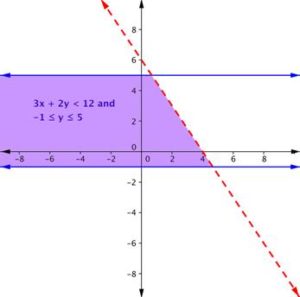
Find the solution to the system [latex] 3x + 2y < 12 [/latex] and [latex] -1 ≤ y ≤ 5 [/latex].
Show Solution
Graph one inequality. First graph the boundary line, then test points.
Remember, because the inequality [latex] 3x + 2y < 12 [/latex] does not include the equal sign, draw a dashed border line.
Testing a point like [latex](0, 0)[/latex] will show that the area below the line is the solution to this inequality.
The inequality [latex] -1 ≤ y ≤ 5[/latex] is actually two inequalities: [latex]−1 ≤ y[/latex], and [latex]y ≤ 5[/latex]. Another way to think of this is y must be between [latex]−1[/latex] and [latex]5[/latex]. The border lines for both are horizontal. The region between those two lines contains the solutions of [latex] -1 ≤ y ≤ 5[/latex]. We make the lines solid because we also want to include [latex]y = −1 [/latex] and [latex] y = 5[/latex].
Graph this region on the same axes as the other inequality.
The purple region shows the set of all solutions of the system.
In the video that follows, we show how to solve another system of inequalities that contains a compound inequality.
Try It
Systems with No Solutions
In the next example, we will show the solution to a system of two inequalities whose boundary lines are parallel to each other. When the graphs of a system of two linear equations are parallel to each other, we found that there was no solution to the system. We will get a similar result for the following system of linear inequalities.
Examples
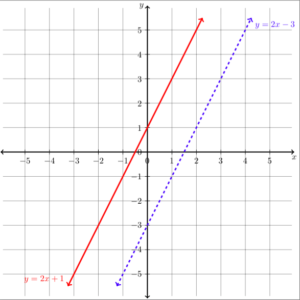
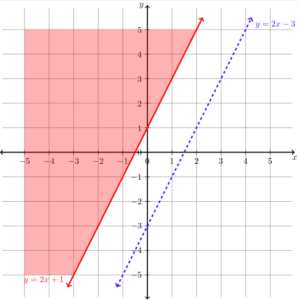
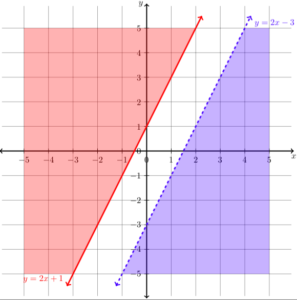
Graph the system [latex]\begin{array}{c}y\ge2x+1\\y\lt2x-3\end{array}[/latex]
Show Solution
The boundary lines for this system are parallel to each other. Note how they have the same slopes.
Plotting the boundary lines will give the graph below. Note that the inequality [latex]y\lt2x-3[/latex] requires that we draw a dashed line, while the inequality [latex]y\ge2x+1[/latex] requires a solid line.
Now we need to shade the regions that represent the inequalities. For the inequality [latex]y\ge2x+1[/latex], we can test a point on either side of the line to see which region to shade. Test [latex]\left(0,0\right)[/latex] to make it easy.
Substitute [latex]\left(0,0\right)[/latex] into [latex]y\ge2x+1[/latex]
This is not true, so we know that we need to shade the other side of the boundary line for the inequality [latex]y\ge2x+1[/latex]. The graph will now look like this:
Now shade the region that shows the solutions to the inequality [latex]y\lt2x-3[/latex]. Again, we can pick [latex]\left(0,0\right)[/latex] to test, because it makes easy algebra.
Substitute [latex]\left(0,0\right)[/latex] into [latex]y\lt2x-3[/latex]
This is not true, so we know that we need to shade the other side of the boundary line for the inequality [latex]y\lt2x-3[/latex]. The graph will now look like this:
This system of inequalities has no points in common so has no solution.
What would the graph look like if the system had looked like this?
Testing the point [latex]\left(0,0\right)[/latex] would return a positive result for the inequality [latex]y\gt2x-3[/latex], and the graph would then look like this:
The pink region is the region of overlap for both inequalities.
Contribute!
Did you have an idea for improving this content? We’d love your input.
Unit 14: Systems of Equations and Inequalities, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/dm-opentext. License: CC BY: Attribution
