Learning Outcomes
- Identify solutions to systems of linear inequalities
Previously, we learned how we can plug an ordered pair into a system of equations to determine whether it is a solution to the system. We can use this same method to determine whether a point is a solution to a system of linear inequalities.
Determine whether an ordered pair is a solution to a system of linear inequalities
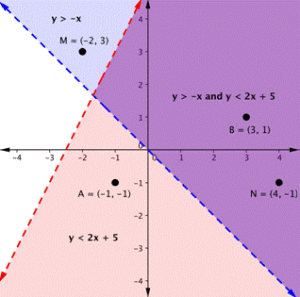
On the graph above, you can see that the points B and N are solutions for the system because their coordinates will make both inequalities true statements.
In contrast, points M and A both lie outside the solution region (purple). While point M is a solution for the inequality [latex]y>−x[/latex] and point A is a solution for the inequality [latex]y<2x+5[/latex], neither point is a solution for the system. The following example shows how to test a point to see whether it is a solution to a system of inequalities.
Example
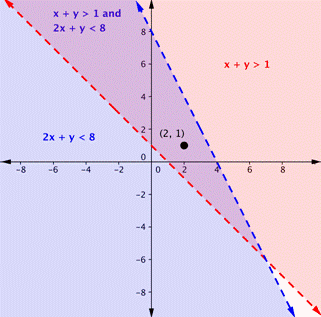
Is the point [latex](2, 1)[/latex] a solution of the system [latex]x+y>1[/latex] and [latex]2x+y<8[/latex]?
Here is a graph of the system in the example above. Notice that [latex](2, 1)[/latex] lies in the purple area, which is the overlapping area for the two inequalities.
Example
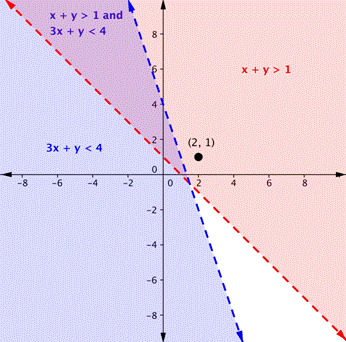
Is the point [latex](2, 1)[/latex] a solution of the system [latex]x+y>1[/latex] and [latex]3x+y<4[/latex]?
Here is a graph of this system. Notice that [latex](2, 1)[/latex] is not in the purple area, which is the overlapping area; it is a solution for one inequality (the red region), but it is not a solution for the second inequality (the blue region).
You can watch the video below for another example of how to verify whether an ordered pair is a solution to a system of linear inequalities.
Summary
- Solutions to systems of linear inequalities are entire regions of points.
- You can verify whether a point is a solution to a system of linear inequalities in the same way you verify whether a point is a solution to a system of equations.
