Learning Outcomes
- Define piecewise function
- Evaluate a piecewise function
- Write a piecewise function given an application
A piecewise function is a function where more than one formula is used to define the output over different pieces of the domain.
We use piecewise functions to describe situations where a rule or relationship changes as the input value crosses certain “boundaries.” Piecewise function are useful in many real-world situations. For example, we often encounter situations in business where the cost per piece of a certain item is discounted once the number ordered exceeds a certain value. Tax brackets are another real-world example of piecewise functions. For example, consider a simple tax system where incomes up to [latex]$10,000[/latex] are taxed at [latex]10\%[/latex] and any additional income is taxed at [latex]20\%[/latex]. The tax on a total income, S, would be [latex]0.1[/latex]S if [latex]S\le[/latex] [latex]$10,000[/latex] and [latex]1000 + 0.2 (S - $10,000)[/latex] if S > [latex]$10,000[/latex].
Piecewise Function
A piecewise function is a function where more than one formula is used to define the output. Each formula has its own domain, and the domain of the function is the union of all of these smaller domains. We notate this idea like this:
[latex] f\left(x\right)=\begin{cases}\text{formula 1 if x is in domain 1}\\ \text{formula 2 if x is in domain 2}\\ \text{formula 3 if x is in domain 3}\end{cases} [/latex]
In piecewise notation, the absolute value function is
Evaluate a Piecewise-Defined Function
In the first example, we will show how to evaluate a piecewise defined function. Note how it is important to pay attention to the domain to determine which expression to use to evaluate the input.
Example
Given the function [latex]f(x)=\begin{cases}7x+3\text{ if }x<0\\7x+6\text{ if }x\ge{0}\end{cases}[/latex], evaluate:
- [latex]f (-1)[/latex]
- [latex]f (0)[/latex]
- [latex]f (2)[/latex]
In the following video, we show how to evaluate several values given a piecewise-defined function.
In the next example, we show how to evaluate a function that models the cost of data transfer for a phone company.
Example
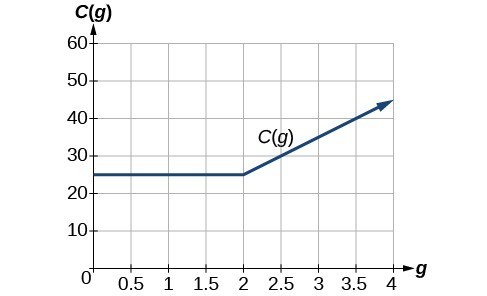
A cell phone company uses the function below to determine the cost, [latex]C[/latex], in dollars for [latex]g[/latex] gigabytes of data transfer.
Find the cost of using [latex]1.5[/latex] gigabytes of data and the cost of using [latex]4[/latex] gigabytes of data.
The function from the previous example is represented in the graph below. We can see where the function changes from a constant to a line with a positive slope at [latex]g=2[/latex]. We plot the graphs for the different formulas on a common set of axes, making sure each formula is applied on its proper domain.
Write a Piecewise-Defined Function
In the last example, we will show how to write a piecewise-defined function that models the price of a guided museum tour.
Example
A museum charges [latex]$5[/latex] per person for a guided tour for a group of [latex]1[/latex] to [latex]9[/latex] people or a fixed $50 fee for a group of [latex]10[/latex] or more people. Write a function relating the number of people, [latex]n[/latex], to the cost, [latex]C[/latex].
A graph of the function for the previous example is shown below. The graph is a diagonal line from [latex]n=0[/latex] to [latex]n=10[/latex] and a constant after that. In this example, the two formulas agree at the meeting point where [latex]n=10[/latex], but not all piecewise functions have this property.

In the following video, we show an example of how to write a piecewise-defined function given a scenario.
How To: Given a piecewise function, write the formula and identify the domain for each interval
- Identify the intervals where different rules apply.
- Determine formulas for the rules that describe how to calculate an output from an input in each interval.
- Use a bracket and “if” statements to write the function.
Summary
- A piecewise function is a function where more than one formula is used to define the output over different pieces of the domain.
- Evaluating a piecewise function means you need to pay close attention to the correct expression used for the given input.
