Learning Outcomes
- Classify solutions and graphs as equations or inequalities
- Identify whether an ordered pair is in the solution set of a linear inequality
Identify the difference between the graph of a linear equation and linear inequality
Recall that solutions to linear inequalities are whole sets of numbers, rather than just one number, like you find with solutions to equalities (equations).
Here is an example from the section on solving linear inequalities:
Solve for p. [latex]4p+5<29[/latex]
[latex]\displaystyle \begin{array}{l}4p+5<\,\,\,29\\\underline{\,\,\,\,\,\,\,\,\,-5\,\,\,\,\,\,\,-5}\\\underline{4p}\,\,\,\,\,\,\,\,<\,\,\underline{24}\,\,\\4\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4\\\,\,\,\,\,\,\,\,\,\,\,p<6\end{array}[/latex]
You can interpret the solution as p can be any number less than six. Now recall that we can graph equations of lines by defining the outputs, [latex]y[/latex], and the inputs, [latex]x[/latex], and writing an equation.
Previously, we showed how to graph the line described by th equation [latex]y=2x+3[/latex] and found that we can construct a never-ending table of values that make points on the line—these are some of the solutions to the equation [latex]y=2x+3[/latex].
| x values | [latex]2x+3[/latex] | y values |
|---|---|---|
| [latex]0[/latex] | [latex]2(0)+3[/latex] | [latex]3[/latex] |
| [latex]1[/latex] | [latex]2(1)+3[/latex] | [latex]5[/latex] |
| [latex]2[/latex] | [latex]2(2)+3[/latex] | [latex]7[/latex] |
| [latex]3[/latex] | [latex]2(3)+3[/latex] | [latex]9[/latex] |
Additionally, we learned how to graph the line that represents all the points that make [latex]y=2x+3[/latex] a true statement.

What if we combined these two ideas—linear inequalities and graphs of lines? First translate the line, [latex]y=2x+3[/latex], into words:
You get y by multiplying [latex]x[/latex] by two and adding three. [latex]y=2x+3[/latex]
How would you translate this inequality into words? [latex]y<2x+3[/latex] For what values of [latex]x[/latex] will you get an output, [latex]y[/latex], that is less than [latex]2[/latex] times [latex]x[/latex] plus three? WOW, that may seem confusing, but keep reading, we’ll help you figure it out. Linear inequalities are different than linear equations, although you can apply what you know about equations to help you understand inequalities. Inequalities and equations are both math statements that compare two values. Equations use the symbol = ; recall that inequalities are represented by the symbols < , ≤ , > , and ≥. One way to visualize two-variable inequalities is to plot them on a coordinate plane. Here is what the inequality [latex]x>y[/latex] looks like. The solution is a region, which is shaded. This region is made up of lots and lots of ordered pairs that all make the statement [latex]x>y[/latex] true.
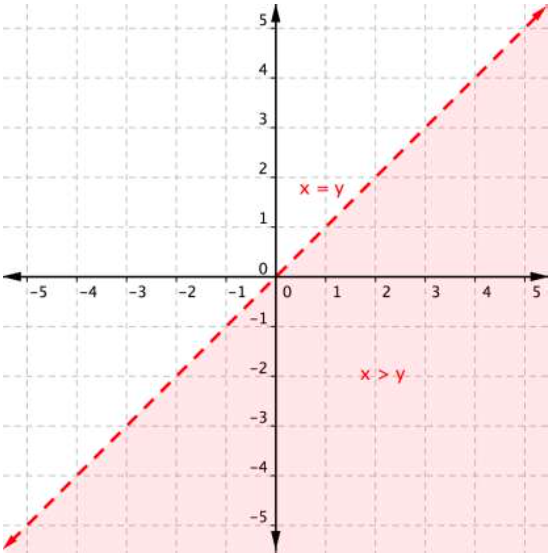
There are a few things to notice here. First, look at the dashed red boundary line: this is the graph of the related linear equation [latex]x=y[/latex]. Next, look at the light red region that is to the right of the line. This region (excluding the line [latex]x=y[/latex]) represents the entire set of solutions for the inequality [latex]x>y[/latex]. Remember how all points on a line are solutions to the linear equation of the line? Well, all points in a region are solutions to the linear inequality representing that region.
Let’s think about it for a moment—if [latex]x>y[/latex], then a graph of [latex]x>y[/latex] will show all ordered pairs [latex](x,y)[/latex] for which the x-coordinate is greater than the y-coordinate.
Identify ordered pairs that are the solution set of a linear inequality
The graph below shows the region [latex]x>y[/latex] as well as some ordered pairs on the coordinate plane. Look at each ordered pair. Is the x-coordinate greater than the y-coordinate? Does the ordered pair sit inside or outside of the shaded region?
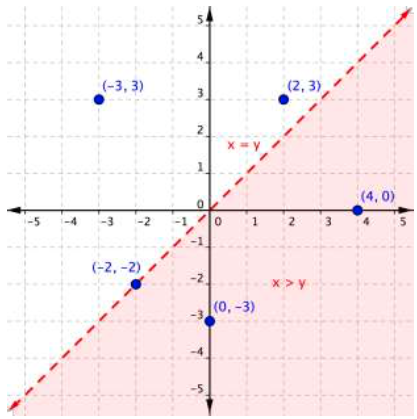
The ordered pairs [latex](4,0)[/latex] and [latex](0,−3)[/latex] lie inside the shaded region. In these ordered pairs, the x-coordinate is larger than the y-coordinate. These ordered pairs are in the solution set of the equation [latex]x>y[/latex].
The ordered pairs [latex](−3,3)[/latex] and [latex](2,3)[/latex] are outside of the shaded area. In these ordered pairs, the x-coordinate is smaller than the y-coordinate, so they are not included in the set of solutions for the inequality.
The ordered pair [latex](−2,−2)[/latex] is on the boundary line. It is not a solution as [latex]−2[/latex] is not greater than [latex]−2[/latex]. However, had the inequality been [latex]x\geq y[/latex] (read as “x is greater than or equal to y”), then [latex](−2,−2)[/latex] would have been included (and the line would have been represented by a solid line, not a dashed line).
Watch the video below for another explanation of the difference between a linear equation and a linear inequality.
Let’s take a look at one more example: the inequality [latex]3x+2y\leq6[/latex]. The graph below shows the region of values that makes this inequality true (shaded red), the boundary line [latex]3x+2y=6[/latex], as well as a handful of ordered pairs. The boundary line is solid this time, because points on the boundary line [latex]3x+2y=6[/latex] will make the inequality [latex]3x+2y\leq6[/latex] true.
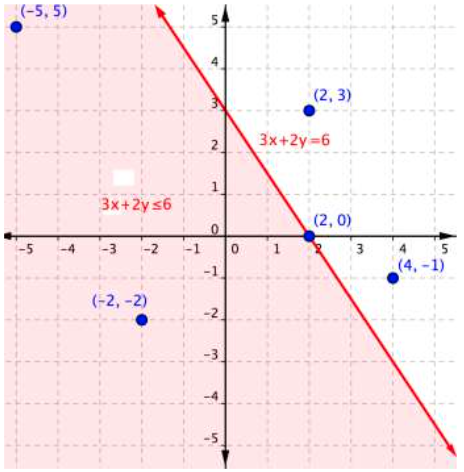
As you did with the previous example, you can substitute the [latex]x[/latex]– and [latex]y[/latex]-values in each of the [latex](x,y)[/latex] ordered pairs into the inequality to find solutions. While you may have been able to do this in your head for the inequality [latex]x>y[/latex], sometimes making a table of values makes sense for more complicated inequalities.
| Ordered Pair | Makes the inequality
[latex]3x+2y\leq6[/latex] a true statement |
Makes the inequality
[latex]3x+2y\leq6[/latex] a false statement |
|---|---|---|
| [latex](−5, 5)[/latex] | [latex]\begin{array}{r}3\left(−5\right)+2\left(5\right)\leq6\\−15+10\leq6\\−5\leq6\end{array}[/latex] | |
| [latex](−2,−2)[/latex] | [latex]\begin{array}{r}3\left(−2\right)+2\left(–2\right)\leq6\\−6+\left(−4\right)\leq6\\–10\leq6\end{array}[/latex] | |
| [latex](2,3)[/latex] | [latex]\begin{array}{r}3\left(2\right)+2\left(3\right)\leq6\\6+6\leq6\\12\leq6\end{array}[/latex] | |
| [latex](2,0)[/latex] | [latex]\begin{array}{r}3\left(2\right)+2\left(0\right)\leq6\\6+0\leq6\\6\leq6\end{array}[/latex] | |
| [latex](4,−1)[/latex] | [latex]\begin{array}{r}3\left(4\right)+2\left(−1\right)\leq6\\12+\left(−2\right)\leq6\\10\leq6\end{array}[/latex] |
If substituting [latex](x,y)[/latex] into the inequality yields a true statement, then the ordered pair is a solution to the inequality, and the point will be plotted within the shaded region or the point will be part of a solid boundary line. A false statement means that the ordered pair is not a solution, and the point will graph outside the shaded region, or the point will be part of a dotted boundary line.
You can watch the following video to see more examples of how to determine whether an ordered pair satisfies a linear inequality.
Example
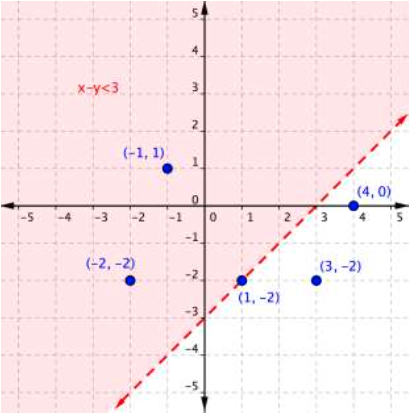
Use the graph to determine which ordered pairs plotted below are solutions of the inequality [latex]x–y<3[/latex].
Watch the video below to see an example of how to use a graph to determine whether an ordered pair is a solutions of a linear inequality in two variables
Example
Is [latex](2,−3)[/latex] a solution of the inequality [latex]y<−3x+1[/latex]?
Try It
Candela Citations
- The Difference Between a Linear Equation and Linear Inequality (Two Variables). Authored by: Mathispower4u. Located at: https://youtu.be/EcrLbRJ2zV0. License: CC BY: Attribution
- Use a Graph Determine Ordered Pair Solutions of a Linear Inequalty in Two Variable. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/GQVdDRVq5_o. License: CC BY: Attribution
- Ex: Determine if Ordered Pairs Satisfy a Linear Inequality. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/-x-zt_yM0RM. License: CC BY: Attribution
- Provided by: Monterey Institute of Technology. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
