Point-Slope Form

We previously learned how to find the equation of a line given the slope of the line and a point on the line.  We did this by substituting the slope and point values into the equation [latex]y=mx+b[/latex] and then solving the equation for b.

We will now show you how you can use either use the slope and a point or just two points to define the equation of the line using point-slope form:

[latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]

This is an important formula, as it will be used in other algebra courses and often in calculus to find the equation of a tangent line. We need only one point and the slope of the line to use the formula. After substituting the slope and the coordinates of one point into the formula, we can simplify it and then write the equation in slope-intercept form.

Now that we know both the slope-intercept form and the point-slope for linear equations, when we are asked to find an equation for a linear function, we can choose which method to use based on the information we are given and our personal preferences. The information provided may be in the form of a graph, a point and a slope, two points, and so on. Let’s look at the graph of the function f below and determine its equation.

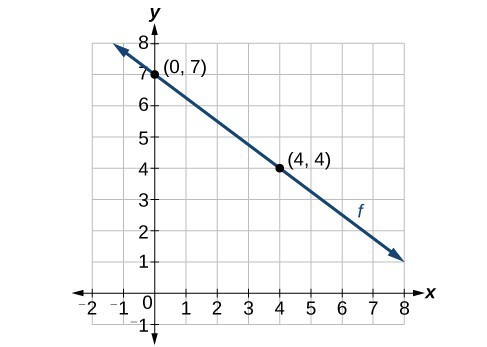
We are not given the slope of the line, but we can choose any two points on the line to find the slope. Choose [latex](0, 7)[/latex] and [latex](4, 4)[/latex]. We can use these points to calculate the slope.

Now we can substitute the slope and the coordinates of one of the points into point-slope form.

If we want to rewrite the equation in slope-intercept form, we would do the following:

If we had wanted to find the equation of the line in slope-intercept form without first using point-slope form, we could have recognized that the line crosses the y-axis when the output value is [latex]7[/latex]. Therefore, b = [latex]7[/latex]. We now have the initial value b and the slope m so we can substitute m and b into slope-intercept form of a line.

The function is [latex]f\left(x\right)=-\dfrac{3}{4}x+7[/latex], and the linear equation would be [latex]y=-\dfrac{3}{4}x+7[/latex].

Let’s take a look at another example like the one above.

Example

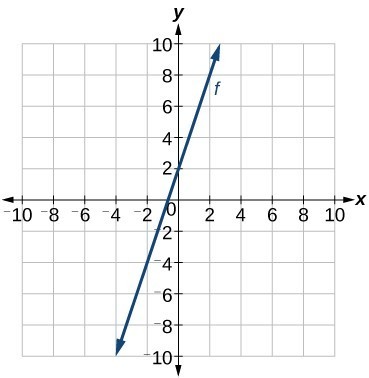
Write an equation for a linear function f given its graph shown below.

Show Solution

Identify two points on the line such as [latex](0, 2)[/latex] and [latex](–2, –4)[/latex]. Use the points to calculate the slope.

[latex]\begin{array}{l}m & =\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}\hfill \\ & =\dfrac{-4 - 2}{-2 - 0}\hfill \\ & =\dfrac{-6}{-2}\hfill \\ & =3\hfill \end{array}[/latex]

Substitute the slope and the coordinates of one of the points into point-slope form.

[latex]\begin{array}{l}y-{y}_{1}=m\left(x-{x}_{1}\right)\\ y-\left(-4\right)=3\left(x-\left(-2\right)\right)\\ y+4=3\left(x+2\right)\end{array}[/latex]

 

We can use algebra to rewrite the equation in slope-intercept form.

[latex]\begin{array}{l}y+4=3\left(x+2\right)\hfill \\ y+4=3x+6\hfill \\ y=3x+2 \hfill \end{array}[/latex]

 

This makes sense because we can see from the graph above that the line crosses the y-axis at the point [latex](0,2)[/latex], which is the y-intercept, so [latex]b=2[/latex]

In our next example, we will start with the slope. Then, we will show how to find the equation of a line when the slope is not given.

Now, let’s look at an example in which we start with two points and find the equation of the line that passes through them.

The following video shows how to write the equation for a line given its slope and a point on the line.

This next video shows another example of writing the equation of a line given two points on the line.

Now that we have seen some examples of how to use the point-slope form of a linear equation, let us look briefly at where the point-slope form comes from.

Recall that the formula for the slope of a line is defined as [latex]m=\dfrac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}[/latex].  For any two points on the same line, the slope formula will always give us the same value for [latex]m[/latex].  With this in mind, let us rewrite the slope equation as [latex]m=\dfrac{y-{y}_{1}}{x-{x}_{1}}[/latex] where [latex](x_1, y_1)[/latex] represents a given point on the line and [latex](x, y)[/latex] represents any other point on our line.  Now, if we multiply both sides of this slope equation by [latex]x-x_1,[/latex] we get the following result:

[latex]m\left(x-{x}_{1}\right)=y-{y}_{1}[/latex]

Which is equivalent to our point-slope form:

[latex]y-{y}_{1}=m\left(x-{x}_{1}\right)[/latex]

We will conclude this section by looking at an example that provides the points of the function using function notation.

In this last video, we show an example of how to write a linear function given two points written with function notation.

Contribute!

Improve this pageLearn More