Learning Outcomes
- Use simple transformations to graph linear functions
Graphing a Linear Function Using Transformations
Another option for graphing linear functions is to use transformations of the identity function [latex]f\left(x\right)=x[/latex] . A function may be transformed by a shift up, down, left, or right. A function may also be transformed using a reflection, stretch, or compression.
Vertical Stretch or Compression
In the equation [latex]f\left(x\right)=mx[/latex], the m is acting as the vertical stretch or compression of the identity function. When m is negative, there is also a vertical reflection of the graph. Notice in the figure below that multiplying the equation of [latex]f\left(x\right)=x[/latex] by m vertically stretches the graph of f by a factor of m units if [latex]m>1[/latex] and vertically compresses the graph of f by a factor of m units if [latex]0<m<1[/latex]. This means the larger the absolute value of m, the steeper the slope. Below you can see a variety of vertical stretches, compressions, and/or reflections on the function [latex]f\left(x\right)=x[/latex].
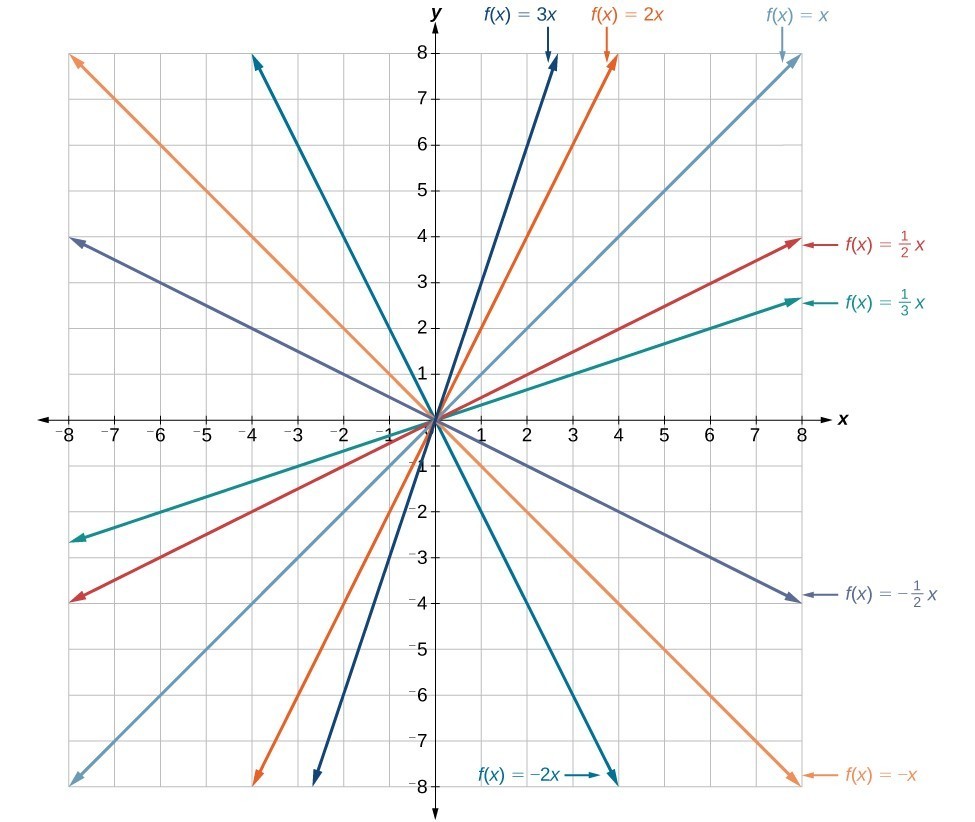
Vertical Shift
In [latex]f\left(x\right)=mx+b[/latex], the b acts as the vertical shift, moving the graph up and down without affecting the slope of the line. Notice in the figure below that adding a value of b to the equation of [latex]f\left(x\right)=x[/latex] shifts the graph of f a total of b units up if b is positive and [latex]|b|[/latex] units down if b is negative. The graph below illustrates vertical shifts of the function [latex]f\left(x\right)=x[/latex].
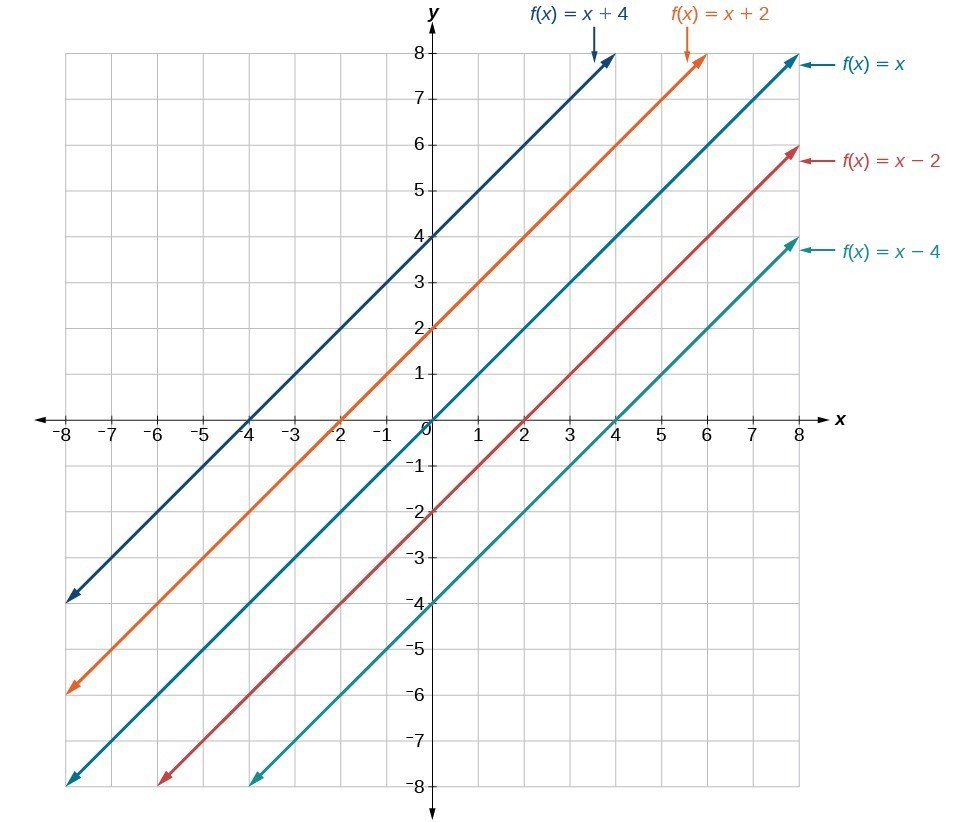
Using vertical stretches or compressions along with vertical shifts is another way to look at identifying different types of linear functions. Although this may not be the easiest way to graph this type of function, it is still important to practice each method.
How To: Given the equation of a linear function, use transformations to graph A linear function OF the form [latex]f\left(x\right)=mx+b[/latex]
- Graph [latex]f\left(x\right)=x[/latex].
- Vertically stretch or compress the graph by a factor of |m|.
- Shift the graph up or down b units.
In the first example, we will see how a vertical compression changes the graph of the identity function.
Example
Describe the transformations to the function [latex]f(x)=\dfrac{2}{3}x[/latex] and draw a graph.
In the next example we will vertically stretch the identity by a factor of [latex]2[/latex].
Example
Describe the transformations to the function [latex]f(x)=2x[/latex] and draw a graph.
Our next example shows how making the slope negative reflects the identity across the y-axis.
Example
Describe the transformations to the function [latex]f(x)=-2x[/latex] and draw a graph.
In our last example, we will combine a vertical compression and a vertical shift to transform [latex]f(x)=x[/latex] into [latex]f\left(x\right)=\dfrac{1}{2}x - 3[/latex] and draw the graph.
Example
Graph [latex]f\left(x\right)=\dfrac{1}{2}x - 3[/latex] using transformations.
The following video example describes another linear transformation of the identity and its corresponding graph.
Q & A
In the example above, could we have sketched the graph by reversing the order of the transformations? No. The order of the transformations follows the order of operations. When the function is evaluated at a given input, the corresponding output is calculated by following the order of operations. This is why we performed the compression first.
Summary
- Vertical compressions of the identity happen when the slope is between [latex]0[/latex] and [latex]1[/latex].
- Vertical stretches of the identity happen when the slope is greater than [latex]1[/latex].
- Reflections happen when the slope is negative.
- Vertical shifts happen when the intercept is not equal to [latex]0[/latex].
- Multiple transformations can be made to a function.





