Learning Outcomes
- Model fraction subtraction
- Subtract fractions with a common denominator
- Subtract fractions with a common denominator that contain variables
Model Fraction Subtraction
Subtracting two fractions with common denominators is much like adding fractions. Think of a pizza that was cut into [latex]12[/latex] slices. Suppose five pieces are eaten for dinner. This means that, after dinner, there are seven pieces (or [latex]{\Large\frac{7}{12}}[/latex] of the pizza) left in the box. If Leonardo eats [latex]2[/latex] of these remaining pieces (or [latex]{\Large\frac{2}{12}}[/latex] of the pizza), how much is left? There would be [latex]5[/latex] pieces left (or [latex]{\Large\frac{5}{12}}[/latex] of the pizza).
[latex]{\Large\frac{7}{12}}-{\Large\frac{2}{12}}={\Large\frac{5}{12}}[/latex]
Let’s use fraction circles to model the same example, [latex]{\Large\frac{7}{12}}-{\Large\frac{2}{12}}[/latex].
Start with seven [latex]{\Large\frac{1}{12}}[/latex] pieces. Take away two [latex]{\Large\frac{1}{12}}[/latex] pieces. How many twelfths are left?
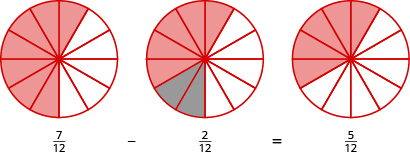
Again, we have five twelfths, [latex]{\Large\frac{5}{12}}[/latex].
Example
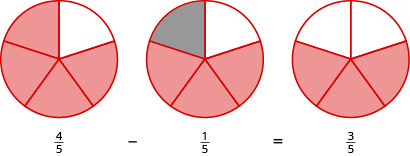
Use fraction circles to find the difference: [latex]{\Large\frac{4}{5}}-{\Large\frac{1}{5}}[/latex]
Solution:
Start with four [latex]{\Large\frac{1}{5}}[/latex] pieces. Take away one [latex]{\Large\frac{1}{5}}[/latex] piece. Count how many fifths are left. There are three [latex]{\Large\frac{1}{5}}[/latex] pieces left, or [latex]{\Large\frac{3}{5}}[/latex].
Try It
Subtract Fractions with a Common Denominator
We subtract fractions with a common denominator in much the same way as we add fractions with a common denominator.
Fraction Subtraction
If [latex]a,b,\text{ and }c[/latex] are numbers where [latex]c\ne 0[/latex], then
[latex]{\Large\frac{a}{c}}-{\Large\frac{b}{c}}={\Large\frac{a-b}{c}}[/latex]
To subtract fractions with a common denominators, we subtract the numerators and place the difference over the common denominator.
Example
Find the difference: [latex]{\Large\frac{23}{24}}-{\Large\frac{14}{24}}[/latex]
Try It
Watch the following video for more examples of subtracting fractions with like denominators.
Subtract Fractions with Variables
Example
Find the difference: [latex]{\Large\frac{y}{6}}-{\Large\frac{1}{6}}[/latex]
Try it
Example
Find the difference: [latex]{\Large-\frac{10}{x}-\frac{4}{x}}[/latex]
Try It
Now lets do an example that involves both addition and subtraction.
Example
Simplify: [latex]{\Large\frac{3}{8}}+\left(-{\Large\frac{5}{8}}\right)-{\Large\frac{1}{8}}[/latex]
Try It
In the next video we show more examples of subtracting fractions with a common denominator. Make note of the second example, it addresses a common mistake made by students when simplifying fractions with variables.
Candela Citations
- Subtract Fractions with Variables and Common Denominators. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/-mLFZT2KgWI. License: CC BY: Attribution
- Question ID: 146190, 146191, 146192, 146249, 146250. Authored by: Alyson Day. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Ex: Subtract Fractions with Like Denominators. Authored by: James Sousa (mathispower4u.com). Located at: https://youtu.be/7CeAQcpOJw0. License: CC BY: Attribution
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757
