Learning Outcomes
- Find the circumference of a circle
- Find the area of a circle
The properties of circles have been studied for over [latex]2,000[/latex] years. All circles have exactly the same shape, but their sizes are affected by the length of the radius, a line segment from the center to any point on the circle. A line segment that passes through a circle’s center connecting two points on the circle is called a diameter. The diameter is twice as long as the radius. See the image below.
The size of a circle can be measured in two ways. The distance around a circle is called its circumference.

Archimedes discovered that for circles of all different sizes, dividing the circumference by the diameter always gives the same number. The value of this number is pi, symbolized by Greek letter [latex]\pi[/latex] (pronounced “pie”). However, the exact value of [latex]\pi[/latex] cannot be calculated since the decimal never ends or repeats (we will learn more about numbers like this in The Properties of Real Numbers.)
Doing the Manipulative Mathematics activity Pi Lab will help you develop a better understanding of pi.
If we want the exact circumference or area of a circle, we leave the symbol [latex]\pi[/latex] in the answer. We can get an approximate answer by substituting [latex]3.14[/latex] as the value of [latex]\pi[/latex]. We use the symbol [latex]\approx[/latex] to show that the result is approximate, not exact.
Properties of Circles
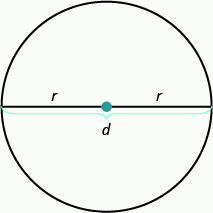
[latex]\begin{array}{c}r\text{ is the length of the radius.}\hfill \\ d\text{ is the length of the diameter.}\hfill \end{array}[/latex]
[latex]\begin{array}{cccc}\text{The circumference is }2\pi \mathit{\text{r}}.\hfill & & & C=2\pi \mathit{\text{r}}\hfill \\ \text{The area is }\pi{\mathit{\text{r}}}^{2}.\hfill & & & A=\pi{\mathit{\text{r}}}^{2}\hfill \end{array}[/latex]
Since the diameter is twice the radius, another way to find the circumference is to use the formula [latex]C=\pi \mathit{\text{d}}[/latex].
Suppose we want to find the exact area of a circle of radius [latex]10[/latex] inches. To calculate the area, we would evaluate the formula for the area when [latex]r=10[/latex] inches and leave the answer in terms of [latex]\pi[/latex].
[latex]\begin{array}{}\\ A=\pi {\mathit{\text{r}}}^{2}\hfill \\ A=\pi \text{(}{10}^{2}\text{)}\hfill \\ A=\pi \cdot 100\hfill \end{array}[/latex]
We write [latex]\pi[/latex] after the [latex]100[/latex]. So the exact value of the area is [latex]A=100\pi[/latex] square inches.
To approximate the area, we would substitute [latex]\pi \approx 3.14[/latex].
[latex]\begin{array}{ccc}A& =& 100\pi \hfill \\ \\ & \approx & 100\cdot 3.14\hfill \\ & \approx & 314\text{ square inches}\hfill \end{array}[/latex]
Remember to use square units, such as square inches, when you calculate the area.
example
A circle has radius [latex]10[/latex] centimeters.Approximate its circumference and area.
Solution
| 1. Find the circumference when [latex]r=10[/latex]. | |
| Write the formula for circumference. | [latex]C=2\pi \mathit{\text{r}}[/latex] |
| Substitute [latex]3.14[/latex] for [latex]\pi[/latex] and 10 for , [latex]r[/latex] . | [latex]C\approx 2\left(3.14\right)\left(10\right)[/latex] |
| Multiply. | [latex]C\approx 62.8\text{ centimeters}[/latex] |
| 2. Find the area when [latex]r=10[/latex]. | |
| Write the formula for area. | [latex]A=\pi {\mathit{\text{r}}}^{2}[/latex] |
| Substitute [latex]3.14[/latex] for [latex]\pi[/latex] and 10 for [latex]r[/latex] . | [latex]A\approx \left(3.14\right){\text{(}10\text{)}}^{2}[/latex] |
| Multiply. | [latex]A\approx 314\text{ square centimeters}[/latex] |
try it
example
A circle has radius [latex]42.5[/latex] centimeters. Approximate its circumference and area.
try it
Watch the following video to see another example of how to find the circumference of a circle.
In the next video example, we find the area of a circle.
Approximate [latex]\pi[/latex] with a Fraction
Convert the fraction [latex]{\Large\frac{22}{7}}[/latex] to a decimal. If you use your calculator, the decimal number will fill up the display and show [latex]3.14285714[/latex]. But if we round that number to two decimal places, we get [latex]3.14[/latex], the decimal approximation of [latex]\pi[/latex]. When we have a circle with radius given as a fraction, we can substitute [latex]{\Large\frac{22}{7}}[/latex] for [latex]\pi[/latex] instead of [latex]3.14[/latex]. And, since [latex]{\Large\frac{22}{7}}[/latex] is also an approximation of [latex]\pi[/latex], we will use the [latex]\approx[/latex] symbol to show we have an approximate value.
example
A circle has radius [latex]{\Large\frac{14}{15}}[/latex] meters. Approximate its circumference and area.
try it
Candela Citations
- Question ID 146611, 146564, 146563. Authored by: Lumen Learning. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
- Examples: Determine the Circumference of a Circle. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/sHtsnC2Mgnk. License: CC BY: Attribution
- Example: Determine the Area of a Circle. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/SIKkWLqt2mQ. License: CC BY: Attribution
- Prealgebra. Provided by: OpenStax. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/caa57dab-41c7-455e-bd6f-f443cda5519c@9.757
