Learning Outcomes
- Find the least common multiple of two numbers by listing multiples
- Find the least common multiple of two numbers by prime factorization
One of the reasons we find multiples and primes is to use them to find the least common multiple of two numbers. This will be useful when we add and subtract fractions with different denominators.
Listing Multiples Method
A common multiple of two numbers is a number that is a multiple of both numbers. Suppose we want to find common multiples of [latex]10[/latex] and [latex]25[/latex]. We can list the first several multiples of each number. Then we look for multiples that are common to both lists—these are the common multiples.
[latex]\begin{array}{c}10\text{ : }10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110\ldots \hfill \\ 25\text{ : }25, 50,75, 100, 125\ldots \hfill \end{array}[/latex]
We see that [latex]50[/latex] and [latex]100[/latex] appear in both lists. They are common multiples of [latex]10[/latex] and [latex]25[/latex]. We would find more common multiples if we continued the list of multiples for each.
The smallest number that is a multiple of two numbers is called the least common multiple (LCM). So the least LCM of [latex]10[/latex] and [latex]25[/latex] is [latex]50[/latex].
Find the least common multiple (LCM) of two numbers by listing multiples
- List the first several multiples of each number.
- Look for multiples common to both lists. If there are no common multiples in the lists, write out additional multiples for each number.
- Look for the smallest number that is common to both lists.
- This number is the LCM.
example
Find the LCM of [latex]15[/latex] and [latex]20[/latex] by listing multiples.
Solution:
List the first several multiples of [latex]15[/latex] and of [latex]20[/latex]. Identify the first common multiple.
[latex]\begin{array}{l}\text{15: }15,30,45,60,75,90,105,120\hfill \\ \text{20: }20,40,60,80,100,120,140,160\hfill \end{array}[/latex]
The smallest number to appear on both lists is [latex]60[/latex], so [latex]60[/latex] is the least common multiple of [latex]15[/latex] and [latex]20[/latex].
Notice that [latex]120[/latex] is on both lists, too. It is a common multiple, but it is not the least common multiple.
try it
In the next video we show an example of how to find the Least Common Multiple by listing multiples of each number.
Prime Factors Method
Another way to find the least common multiple of two numbers is to use their prime factors. We’ll use this method to find the LCM of [latex]12[/latex] and [latex]18[/latex].
We start by finding the prime factorization of each number.
[latex]12=2\cdot 2\cdot 318=2\cdot 3\cdot 3[/latex]
Then we write each number as a product of primes, matching primes vertically when possible.
[latex]\begin{array}{l}12=2\cdot 2\cdot 3\hfill \\ 18=2\cdot 3\cdot 3\end{array}[/latex]
Now we bring down the primes in each column. The LCM is the product of these factors.
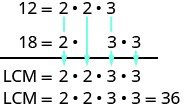
Notice that the prime factors of [latex]12[/latex] and the prime factors of [latex]18[/latex] are included in the LCM. By matching up the common primes, each common prime factor is used only once. This ensures that [latex]36[/latex] is the least common multiple.
Find the LCM using the prime factors method
- Find the prime factorization of each number.
- Write each number as a product of primes, matching primes vertically when possible.
- Bring down the primes in each column.
- Multiply the factors to get the LCM.
example
Find the LCM of [latex]15[/latex] and [latex]18[/latex] using the prime factors method.
try it
example
Find the LCM of [latex]50[/latex] and [latex]100[/latex] using the prime factors method.
try it
In the next video we show how to find the Least Common Multiple by using prime factorization.




