Writing and Identifying Characteristics of Decimals

Name Decimals

In the following exercises, name each decimal.

1. [latex]5.5[/latex]
   Show Solution

   five and five tenths
2. [latex]7.8[/latex]
3. [latex]5.01[/latex]
   Show Solution

   five and one hundredth
4. [latex]14.02[/latex]
5. [latex]8.71[/latex]
   Show Solution

   eight and seventy-one hundredths
6. [latex]2.64[/latex]
7. [latex]0.002[/latex]
   Show Solution

   two thousandths
8. [latex]0.005[/latex]
9. [latex]0.381[/latex]
   Show Solution

   three hundred eighty-one thousandths
10. [latex]0.479[/latex]
11. [latex]-17.9[/latex]
    Show Solution

    negative seventeen and nine tenths
12. [latex]-31.4[/latex]

Write Decimals

In the following exercises, translate the name into a decimal number.

1. Eight and three hundredths
   Show Solution

   8.03
2. Nine and seven hundredths
3. Twenty-nine and eighty-one hundredths
   Show Solution

   29.81
4. Sixty-one and seventy-four hundredths
5. Seven tenths
   Show Solution

   0.7
6. Six tenths
7. One thousandth
   Show Solution

   0.001
8. Nine thousandths
9. Twenty-nine thousandths
   Show Solution

   0.029
10. Thirty-five thousandths
11. Negative eleven and nine ten-thousandths
    Show Solution

    −11.0009
12. Negative fifty-nine and two ten-thousandths
13. Thirteen and three hundred ninety-five ten thousandths
    Show Solution

    13.0395
14. Thirty and two hundred seventy-nine thousandths

Convert Decimals to Fractions or Mixed Numbers

In the following exercises, convert each decimal to a fraction or mixed number.

1. [latex]1.99[/latex]
   Show Solution

   [latex]1\Large\frac{99}{100}[/latex]
2. [latex]5.83[/latex]
3. [latex]15.7[/latex]
   Show Solution

   [latex]15\Large\frac{7}{10}[/latex]
4. [latex]18.1[/latex]
5. [latex]0.239[/latex]
   Show Solution

   [latex]\Large\frac{239}{1000}[/latex]
6. [latex]0.373[/latex]
7. [latex]0.13[/latex]
   Show Solution

   [latex]\Large\frac{13}{100}[/latex]
8. [latex]0.19[/latex]
9. [latex]0.011[/latex]
   Show Solution

   [latex]\Large\frac{11}{1000}[/latex]
10. [latex]0.049[/latex]
11. [latex]-0.00007[/latex]
    Show Solution

    [latex]-\Large\frac{7}{100000}[/latex]
12. [latex]-0.00003[/latex]
13. [latex]6.4[/latex]
    Show Solution

    [latex]6\Large\frac{2}{5}[/latex]
14. [latex]5.2[/latex]
15. [latex]7.05[/latex]
    Show Solution

    [latex]7\Large\frac{1}{20}[/latex]
16. [latex]9.04[/latex]
17. [latex]4.006[/latex]
    Show Solution

    [latex]4\Large\frac{3}{500}[/latex]
18. [latex]2.008[/latex]
19. [latex]10.25[/latex]
    Show Solution

    [latex]10\Large\frac{1}{4}[/latex]
20. [latex]12.75[/latex]
21. [latex]1.324[/latex]
    Show Solution

    [latex]1\Large\frac{81}{250}[/latex]
22. [latex]2.482[/latex]
23. [latex]14.125[/latex]
    Show Solution

    [latex]14\Large\frac{1}{8}[/latex]
24. [latex]20.375[/latex]

Locate Decimals on the Number Line

In the following exercises, locate each number on a number line.

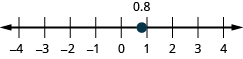
1. [latex]0.8[/latex]
   Show Solution

   
2. [latex]0.3[/latex]
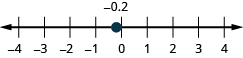
3. [latex]-0.2[/latex]
   Show Solution

   
4. [latex]-0.9[/latex]
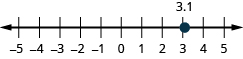
5. [latex]3.1[/latex]
   Show Solution

   
6. [latex]2.7[/latex]
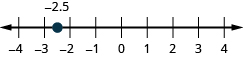
7. [latex]-2.5[/latex]
   Show Solution

   
8. [latex]-1.6[/latex]

Order Decimals

In the following exercises, order each of the following pairs of numbers, using [latex]<\text{or}>[/latex];.

1. [latex]0.9\text{__}0.6[/latex]
   Show Solution

   >
2. [latex]0.7\text{__}0.8[/latex]
3. [latex]0.37\text{__}0.63[/latex]
   Show Solution

   <
4. [latex]0.86\text{__}0.69[/latex]
5. [latex]0.6\text{__}0.59[/latex]
   Show Solution

   >
6. [latex]0.27\text{__}0.3[/latex]
7. [latex]0.91\text{__}0.901[/latex]
   Show Solution

   >
8. [latex]0.415\text{__}0.41[/latex]
9. [latex]-0.5\text{__} - 0.3[/latex]
   Show Solution

   <
10. [latex]-0.1\text{__} - 0.4[/latex]
11. [latex]-0.62\text{__} - 0.619[/latex]
    Show Solution

    <
12. [latex]-7.31\text{__} - 7.3[/latex]

Round Decimals

In the following exercises, round each number to the nearest tenth.

1. [latex]0.67[/latex]
   Show Solution

   0.7
2. [latex]0.49[/latex]
3. [latex]2.84[/latex]
   Show Solution

   2.8
4. [latex]4.63[/latex]

In the following exercises, round each number to the nearest hundredth.

1. [latex]0.845[/latex]
   Show Solution

   0.85
2. [latex]0.761[/latex]
3. [latex]5.7932[/latex]
   Show Solution

   5.79
4. [latex]3.6284[/latex]
5. [latex]0.299[/latex]
   Show Solution

   0.30
6. [latex]0.697[/latex]
7. [latex]4.098[/latex]
   Show Solution

   4.10
8. [latex]7.096[/latex]

In the following exercises, round each number to the nearest ⓐ hundredth ⓑ tenth ⓒ whole number.

1. [latex]5.781[/latex]
   Show Solution

   ⓐ 5.78 ⓑ 5.8 ⓒ 6
2. [latex]1.638[/latex]
3. [latex]63.479[/latex]
   Show Solution

   ⓐ 63.48 ⓑ 63.5 ⓒ 63
4. [latex]84.281[/latex]

Operations on Decimals

Add and Subtract Decimals

In the following exercises, add or subtract.

1. [latex]16.92+7.56[/latex]
   Show Solution

   24.48
2. [latex]18.37+9.36[/latex]
3. [latex]256.37 - 85.49[/latex]
   Show Solution

   170.88
4. [latex]248.25 - 91.29[/latex]
5. [latex]21.76 - 30.99[/latex]
   Show Solution

   −9.23
6. [latex]15.35 - 20.88[/latex]
7. [latex]37.5+12.23[/latex]
   Show Solution

   49.73
8. [latex]38.6+13.67[/latex]
9. [latex]-16.53 - 24.38[/latex]
   Show Solution

   −40.91
10. [latex]-19.47 - 32.58[/latex]
11. [latex]-38.69+31.47[/latex]
    Show Solution

    −7.22
12. [latex]-29.83+19.76[/latex]
13. [latex]-4.2+\left(-9.3\right)[/latex]
    Show Solution

    −13.5
14. [latex]-8.6+\left(-8.6\right)[/latex]
15. [latex]100 - 64.2[/latex]
    Show Solution

    35.8
16. [latex]100 - 65.83[/latex]
17. [latex]72.5 - 100[/latex]
    Show Solution

    −27.5
18. [latex]86.2 - 100[/latex]
19. [latex]15+0.73[/latex]
    Show Solution

    15.73
20. [latex]27+0.87[/latex]
21. [latex]2.51+40[/latex]
    Show Solution

    42.51
22. [latex]9.38+60[/latex]
23. [latex]91.75-\left(-10.462\right)[/latex]
    Show Solution

    102.212
24. [latex]94.69-\left(-12.678\right)[/latex]
25. [latex]55.01 - 3.7[/latex]
    Show Solution

    51.31
26. [latex]59.08 - 4.6[/latex]
27. [latex]2.51 - 7.4[/latex]
    Show Solution

    −4.89
28. [latex]3.84 - 6.1[/latex]

Multiply Decimals

In the following exercises, multiply.

1. [latex]\left(0.3\right)\left(0.4\right)[/latex]
   Show Solution

   0.12
2. [latex]\left(0.6\right)\left(0.7\right)[/latex]
3. [latex]\left(0.24\right)\left(0.6\right)[/latex]
   Show Solution

   0.144
4. [latex]\left(0.81\right)\left(0.3\right)[/latex]
5. [latex]\left(5.9\right)\left(7.12\right)[/latex]
   Show Solution

   42.008
6. [latex]\left(2.3\right)\left(9.41\right)[/latex]
7. [latex]\left(8.52\right)\left(3.14\right)[/latex]
   Show Solution

   26.7528
8. [latex]\left(5.32\right)\left(4.86\right)[/latex]
9. [latex]\text{(-4.3)(2.71)}[/latex]
   Show Solution

   −11.653
10. [latex]\left(-8.5\right)\left(1.69\right)[/latex]
11. [latex]\text{(-5.18)(-65.23)}[/latex]
    Show Solution

    337.8914
12. [latex]\left(-9.16\right)\left(-68.34\right)[/latex]
13. [latex]\left(0.09\right)\left(24.78\right)[/latex]
    Show Solution

    2.2302
14. [latex]\left(0.04\right)\left(36.89\right)[/latex]
15. [latex]\left(0.06\right)\left(21.75\right)[/latex]
    Show Solution

    1.305
16. [latex]\left(0.08\right)\left(52.45\right)[/latex]
17. [latex]\left(9.24\right)\left(10\right)[/latex]
    Show Solution

    92.4
18. [latex]\left(6.531\right)\left(10\right)[/latex]
19. [latex]\left(55.2\right)\left(1,000\right)[/latex]
    Show Solution

    55,200
20. [latex]\left(99.4\right)\left(1,000\right)[/latex]

Divide Decimals

In the following exercises, divide.

1. [latex]0.15\div 5[/latex]
   Show Solution

   0.03
2. [latex]0.27\div 3[/latex]
3. [latex]4.75\div 25[/latex]
   Show Solution

   0.19
4. [latex]12.04\div 43[/latex]
5. [latex]{$8.49}\div 12[/latex]
   Show Solution

   $0.71
6. [latex]{$16.99}\div 9[/latex]
7. [latex]{$117.25}\div 48[/latex]
   Show Solution

   $2.44
8. [latex]{$109.24}\div 36[/latex]
9. [latex]0.6\div 0.2[/latex]
   Show Solution

   3
10. [latex]0.8\div 0.4[/latex]
11. [latex]1.44\div \left(-0.3\right)[/latex]
    Show Solution

    −4.8
12. [latex]1.25\div \left(-0.5\right)[/latex]
13. [latex]-1.75\div \left(-0.05\right)[/latex]
    Show Solution

    35
14. [latex]-1.15\div \left(-0.05\right)[/latex]
15. [latex]5.2\div 2.5[/latex]
    Show Solution

    2.08
16. [latex]6.5\div 3.25[/latex]
17. [latex]12\div 0.08[/latex]
    Show Solution

    150
18. [latex]5\div 0.04[/latex]
19. [latex]11\div 0.55[/latex]
    Show Solution

    20
20. [latex]14\div 0.35[/latex]

Mixed Practice

In the following exercises, simplify.

1. [latex]6\left(12.4 - 9.2\right)[/latex]
   Show Solution

   19.2
2. [latex]3\left(15.7 - 8.6\right)[/latex]
3. [latex]24\left(0.5\right)+{\left(0.3\right)}^{2}[/latex]
   Show Solution

   12.09
4. [latex]35\left(0.2\right)+{\left(0.9\right)}^{2}[/latex]
5. [latex]1.15\left(26.83+1.61\right)[/latex]
   Show Solution

   32.706
6. [latex]1.18\left(46.22+3.71\right)[/latex]
7. [latex]{$45}+0.08\left({$45}\right)[/latex]
   Show Solution

   $48.60
8. [latex]{$63}+0.18\left({$63}\right)[/latex]
9. [latex]18\div \left(0.75+0.15\right)[/latex]
   Show Solution

   20
10. [latex]27\div \left(0.55+0.35\right)[/latex]
11. [latex]\left(1.43+0.27\right)\div \left(0.9 - 0.05\right)[/latex]
    Show Solution

    2
12. [latex]\left(1.5 - 0.06\right)\div \left(0.12+0.24\right)[/latex]
13. [latex]\left[{$75.42}+0.18\left({$75.42}\right)\right]\div 5[/latex]
    Show Solution

    $17.80
14. [latex]\left[{$56.31}+0.22\left({$56.31}\right)\right]\div 4[/latex]

Use Decimals in Money Applications

In the following exercises, use the strategy for applications to solve.

Spending money

Brenda got [latex]{$40}[/latex] from the ATM. She spent [latex]{$15.11}[/latex] on a pair of earrings. How much money did she have left?

Spending money

Marissa found [latex]{$20}[/latex] in her pocket. She spent [latex]{$4.82}[/latex] on a smoothie. How much of the [latex]{$20}[/latex] did she have left?

Shopping

Adam bought a t-shirt for [latex]{$18.49}[/latex] and a book for [latex]{$8.92}[/latex] The sales tax was [latex]{$1.65}[/latex]. How much did Adam spend?

Restaurant

Roberto’s restaurant bill was [latex]{$20.45}[/latex] for the entrée and [latex]{$3.15}[/latex] for the drink. He left a [latex]{$4.40}[/latex] tip. How much did Roberto spend?

Coupon

Emily bought a box of cereal that cost [latex]{$4.29}[/latex]. She had a coupon for [latex]{$0.55}[/latex] off, and the store doubled the coupon. How much did she pay for the box of cereal?

Coupon

Diana bought a can of coffee that cost [latex]{$7.99}[/latex]. She had a coupon for [latex]{$0.75}[/latex] off, and the store doubled the coupon. How much did she pay for the can of coffee?

Diet

Leo took part in a diet program. He weighed [latex]190[/latex] pounds at the start of the program. During the first week, he lost [latex]4.3[/latex] pounds. During the second week, he had lost [latex]2.8[/latex] pounds. The third week, he gained [latex]0.7[/latex] pounds. The fourth week, he lost [latex]1.9[/latex] pounds. What did Leo weigh at the end of the fourth week?

Snowpack

On April [latex]1[/latex], the snowpack at the ski resort was [latex]4[/latex] meters deep, but the next few days were very warm. By April [latex]5[/latex], the snow depth was [latex]1.6[/latex] meters less. On April [latex]8[/latex], it snowed and added [latex]2.1[/latex] meters of snow. What was the total depth of the snow?

Coffee

Noriko bought [latex]4[/latex] coffees for herself and her co-workers. Each coffee was [latex]{$3.75}[/latex]. How much did she pay for all the coffees?

Subway Fare

Arianna spends [latex]{$4.50}[/latex] per day on subway fare. Last week she rode the subway [latex]6[/latex] days. How much did she spend for the subway fares?

Income

Mayra earns [latex]{$9.25}[/latex] per hour. Last week she worked [latex]32[/latex] hours. How much did she earn?

Income

Peter earns [latex]{$8.75}[/latex] per hour. Last week he worked [latex]19[/latex] hours. How much did he earn?

Hourly Wage

Alan got his first paycheck from his new job. He worked [latex]30[/latex] hours and earned [latex]{$382.50}[/latex]. How much does he earn per hour?

Hourly Wage

Maria got her first paycheck from her new job. She worked [latex]25[/latex] hours and earned [latex]{$362.50}[/latex]. How much does she earn per hour?

Restaurant

Jeannette and her friends love to order mud pie at their favorite restaurant. They always share just one piece of pie among themselves. With tax and tip, the total cost is [latex]\$6.00[/latex]. How much does each girl pay if the total number sharing the mud pie is

1. [latex]2?[/latex]
   Show Solution

   $3
2. [latex]3?[/latex]
   Show Solution

   $2
3. [latex]4?[/latex]
   Show Solution

   $1.50
4. [latex]5?[/latex]
   Show Solution

   $1.20
5. [latex]6?[/latex]
   Show Solution

   $1

Pizza

Alex and his friends go out for pizza and video games once a week. They share the cost of a [latex]\$15.60[/latex] pizza equally. How much does each person pay if the total number sharing the pizza is

1.  [latex]2?[/latex]
2. [latex]3?[/latex]
3. [latex]4?[/latex]
4. [latex]5?[/latex]
5.  [latex]6?[/latex]

Fast Food

At their favorite fast food restaurant, the Carlson family orders [latex]4[/latex] burgers that cost [latex]{$3.29}[/latex] each and [latex]2[/latex] orders of fries at [latex]{$2.74}[/latex] each. What is the total cost of the order?

Home Goods

Chelsea needs towels to take with her to college. She buys [latex]2[/latex] bath towels that cost [latex]{$9.99}[/latex] each and [latex]6[/latex] washcloths that cost [latex]{$2.99}[/latex] each. What is the total cost for the bath towels and washcloths?

Zoo

The Lewis and Chousmith families are planning to go to the zoo together. Adult tickets cost [latex]{$29.95}[/latex] and children’s tickets cost [latex]{$19.95}[/latex]. What will the total cost be for [latex]4[/latex] adults and [latex]7[/latex] children?

Ice Skating

Jasmine wants to have her birthday party at the local ice skating rink. It will cost [latex]{$8.25}[/latex] per child and [latex]{$12.95}[/latex] per adult. What will the total cost be for [latex]12[/latex] children and [latex]3[/latex] adults?

Exploring The Relationship Between Decimals and Fractions

Convert Fractions to Decimals

In the following exercises, convert each fraction to a decimal.

1. [latex]\Large\frac{2}{5}[/latex]
   Show Solution

   0.4
2. [latex]\Large\frac{4}{5}[/latex]
3. [latex]-\Large\frac{3}{8}[/latex]
   Show Solution

   −0.375
4. [latex]-\Large\frac{5}{8}[/latex]
5. [latex]\Large\frac{17}{20}[/latex]
   Show Solution

   0.85
6. [latex]\Large\frac{13}{20}[/latex]
7. [latex]\Large\frac{11}{4}[/latex]
   Show Solution

   2.75
8. [latex]\Large\frac{17}{4}[/latex]
9. [latex]-\Large\frac{310}{25}[/latex]
   Show Solution

   −12.4
10. [latex]-\Large\frac{284}{25}[/latex]
11. [latex]\Large\frac{5}{9}[/latex]
    Show Solution

    [latex]0.\stackrel{-}{5}[/latex]
12. [latex]\Large\frac{2}{9}[/latex]
13. [latex]\Large\frac{15}{11}[/latex]
    Show Solution

    [latex]1.\stackrel{\text{-}}{36}[/latex]
14. [latex]\Large\frac{18}{11}[/latex]
15. [latex]\Large\frac{15}{111}[/latex]
    Show Solution

    [latex]0.\stackrel{\text{-}}{135}[/latex]
16. [latex]\Large\frac{25}{111}[/latex]

Convert Fractions to Decimals and Simplify

In the following exercises, simplify the expression.

1. [latex]\Large\frac{1}{2}\normalsize+6.5[/latex]
   Show Solution

   7
2. [latex]\Large\frac{1}{4}\normalsize+10.75[/latex]
3. [latex]2.4+\Large\frac{5}{8}[/latex]
   Show Solution

   3.025
4. [latex]3.9+\Large\frac{9}{20}[/latex]
5. [latex]9.73+\Large\frac{17}{20}[/latex]
   Show Solution

   10.58
6. [latex]6.29+\Large\frac{21}{40}[/latex]

Order Decimals and Fractions

In the following exercises, order each pair of numbers, using [latex]<[/latex]; or [latex]\text{>.}[/latex]

1. [latex]\Large\frac{1}{8}\normalsize\text{___}0.8[/latex]
   Show Solution

   <
2. [latex]\Large\frac{1}{4}\normalsize\text{___}0.4[/latex]
3. [latex]\Large\frac{2}{5}\normalsize\text{___}0.25[/latex]
   Show Solution

   >
4. [latex]\Large\frac{3}{5}\normalsize\text{___}0.35[/latex]
5. [latex]\text {0.725___}\Large\frac{3}{4}[/latex]
   Show Solution

   <
6. [latex]\text {0.92___}\Large\frac{7}{8}[/latex]
7. [latex]\text {0.66___}\Large\frac{2}{3}[/latex]
   Show Solution

   <
8. [latex]\text {0.83___}\Large\frac{5}{6}[/latex]
9. [latex]\text {-0.75___}-\Large\frac{4}{5}[/latex]
   Show Solution

   >
10. [latex]\text {-0.44___}-\Large\frac{9}{20}[/latex]
11. [latex]-\Large\frac{3}{4}\normalsize\text{___} - 0.925[/latex]
    Show Solution

    >
12. [latex]-\Large\frac{2}{3}\normalsize\text{___} - 0.632[/latex]

Order Decimals and Fractions

In the following exercises, write each set of numbers in order from least to greatest.

1. [latex]\Large\frac{3}{5}\normalsize ,\Large\frac{9}{16}\normalsize,0.55[/latex]
   Show Solution

   [latex]0.55,\Large\frac{9}{16}\normalsize ,\Large\frac{3}{5}[/latex]
2. [latex]\Large\frac{3}{8}\normalsize ,\Large\frac{7}{20}\normalsize ,0.36[/latex]
3. [latex]0.702,\Large\frac{13}{20}\normalsize ,\Large\frac{5}{8}[/latex]
   Show Solution

   [latex]\Large\frac{5}{8}\normalsize ,\Large\frac{13}{20}\normalsize ,0.702[/latex]
4. [latex]0.15,\Large\frac{3}{16}\normalsize ,\Large\frac{1}{5}[/latex]
5. [latex]-0.3,-\Large\frac{1}{3}\normalsize ,-\Large\frac{7}{20}[/latex]
   Show Solution

   [latex]-\Large\frac{7}{20}\normalsize ,-\Large\frac{1}{3}\normalsize,-0.3[/latex]
6. [latex]-0.2,-\Large\frac{3}{20}\normalsize ,-\Large\frac{1}{6}[/latex]
7. [latex]-\Large\frac{3}{4}\normalsize ,-\Large\frac{7}{9}\normalsize,-0.7[/latex]
   Show Solution

   [latex]-\Large\frac{7}{9}\normalsize ,-\Large\frac{3}{4}\normalsize ,-0.7[/latex]
8. [latex]-\Large\frac{8}{9}\normalsize ,-\Large\frac{4}{5}\normalsize,-0.9[/latex]

Simplify Expressions Using the Order of Operations

In the following exercises, simplify.

1. [latex]10\left(25.1 - 43.8\right)[/latex]
   Show Solution

   −187
2. [latex]30\left(18.1 - 32.5\right)[/latex]
3. [latex]62\left(9.75 - 4.99\right)[/latex]
   Show Solution

   295.12
4. [latex]42\left(8.45 - 5.97\right)[/latex]
5. [latex]\Large\frac{3}{4}\normalsize\left(12.4 - 4.2\right)[/latex]
   Show Solution

   6.15
6. [latex]\Large\frac{4}{5}\normalsize\left(8.6+3.9\right)[/latex]
7. [latex]\Large\frac{5}{12}\normalsize\left(30.58+17.9\right)[/latex]
   Show Solution

   20.2
8. [latex]\Large\frac{9}{16}\normalsize\left(21.96 - 9.8\right)[/latex]
9. [latex]10\div 0.1+\left(1.8\right)4-{\left(0.3\right)}^{2}[/latex]
   Show Solution

   107.11
10. [latex]5\div 0.5+\left(3.9\right)6-{\left(0.7\right)}^{2}[/latex]
11. [latex]\left(37.1+52.7\right)\div \left(12.5\div 62.5\right)[/latex]
    Show Solution

    449
12. [latex]\left(11.4+16.2\right)\div \left(18\div 60\right)[/latex]
13. [latex]{\Large\left(\frac{1}{5}\right)}^{2}\normalsize+\left(1.4\right)\left(6.5\right)[/latex]
    Show Solution

    9.14
14. [latex]{\Large\left(\frac{1}{2}\right)}^{2}\normalsize+\left(2.1\right)\left(8.3\right)[/latex]
15. [latex]-\Large\frac{9}{10}\normalsize\cdot\Large\frac{8}{15}\normalsize+0.25[/latex]
    Show Solution

    −0.23
16. [latex]-\Large\frac{3}{8}\normalsize\cdot\Large\frac{14}{15}\normalsize+0.72[/latex]

Mixed Practice

In the following exercises, simplify. Give the answer as a decimal.

1. [latex]3\Large\frac{1}{4}\normalsize -6.5[/latex]
   Show Solution

   −3.25
2. [latex]5\Large\frac{2}{5}\normalsize -8.75[/latex]
3. [latex]10.86\div\Large\frac{2}{3}[/latex]
   Show Solution

   16.29
4. [latex]5.79\div\Large\frac{3}{4}[/latex]
5. [latex]\Large\frac{7}{8}\normalsize\left(103.48\right)+1\Large\frac{1}{2}\normalsize\left(361\right)[/latex]
   Show Solution

   632.045
6. [latex]\Large\frac{5}{16}\normalsize\left(117.6\right)+2\Large\frac{1}{3}\normalsize\left(699\right)[/latex]
7. [latex]3.6\left(\Large\frac{9}{8}\normalsize-2.72\right)[/latex]
   Show Solution

   −5.742
8. [latex]5.1\left(\Large\frac{12}{5}\normalsize-3.91\right)[/latex]

Find the Circumference and Area of Circles

In the following exercises, approximate the a) circumference and b) area of each circle. If measurements are given in fractions, leave answers in fraction form.

1. [latex]\text{radius}=\text{5 in.}[/latex]
   Show Solution

   ⓐ 31.4 in ⓑ 78.5 sq.in.
2. [latex]\text{radius}=\text{20 in.}[/latex]
3. [latex]\text{radius}=\text{9 ft.}[/latex]
   Show Solution

   ⓐ 56.52.ft. ⓑ 254.34 sq.ft.
4. [latex]\text{radius}=\text{4 ft.}[/latex]
5. [latex]\text{radius}=\text{46 cm}[/latex]
   Show Solution

   ⓐ 288.88 cm ⓑ 6644.24 sq.cm
6. [latex]\text{radius}=\text{38 cm}[/latex]
7. [latex]\text{radius}=\text{18.6 m}[/latex]
   Show Solution

   ⓐ 116.808 m ⓑ 1086.3144 sq.m
8. [latex]\text{radius}=\text{57.3 m}[/latex]
9. [latex]\text{radius}=\Large\frac{7}{10}\normalsize\text{mile}[/latex]
   Show Solution

   ⓐ [latex]\Large\frac{22}{5}\normalsize\text{mile}[/latex] ⓑ [latex]\Large\frac{77}{50}\normalsize\text{sq.mile}[/latex]
10. [latex]\text{radius}=\Large\frac{7}{11}\normalsize\text{mile}[/latex]
11. [latex]\text{radius}=\Large\frac{3}{8}\normalsize\text{yard}[/latex]
    Show Solution

    ⓐ [latex]\Large\frac{33}{14}\normalsize\text{yard}[/latex] ⓑ [latex]\Large\frac{99}{224}\normalsize\text{sq.yard}[/latex]
12. [latex]\text{radius}=\Large\frac{5}{12}\normalsize\text{yard}[/latex]
13. [latex]\text{diameter}=\Large\frac{5}{6}\normalsize\text{m}[/latex]
    Show Solution

    ⓐ [latex]\Large\frac{55}{21}\normalsize\text{m}[/latex] ⓑ [latex]\Large\frac{275}{504}\normalsize\text{sq.m}[/latex]
14. [latex]\text{diameter}=\Large\frac{3}{4}\normalsize\text{m}[/latex]

Solving Equations with Decimals

Calculate the Mean of a Set of Numbers

In the following exercises, find the mean.

1. [latex]3[/latex] , [latex]8[/latex] , [latex]2[/latex] , [latex]2[/latex] , [latex]5[/latex]
   Show Solution

   4
2. [latex]6[/latex] , [latex]1[/latex] , [latex]9[/latex] , [latex]3[/latex] , [latex]4[/latex] , [latex]7[/latex]
3. [latex]65[/latex] , [latex]13[/latex] , [latex]48[/latex] , [latex]32[/latex] , [latex]19[/latex] , [latex]33[/latex]
   Show Solution

   35
4. [latex]34[/latex] , [latex]45[/latex] , [latex]29[/latex] , [latex]61[/latex] , and [latex]41[/latex]
5. [latex]202[/latex] , [latex]241[/latex] , [latex]265[/latex] , [latex]274[/latex]
   Show Solution

   245.5
6. [latex]525[/latex] , [latex]532[/latex] , [latex]558[/latex] , [latex]574[/latex]
7. [latex]12.45[/latex] , [latex]12.99[/latex] , [latex]10.50[/latex] , [latex]11.25[/latex] , [latex]9.99[/latex] , [latex]12.72[/latex]
   Show Solution

   11.65
8. [latex]28.8[/latex] , [latex]32.9[/latex] , [latex]32.5[/latex] , [latex]27.9[/latex] , [latex]30.4[/latex] , [latex]32.5[/latex] , [latex]31.6[/latex] , [latex]32.7[/latex]

Calculate the Mean of a Set of Numbers in Applications

In the following exercises, find the mean.

1. Four girls leaving a mall were asked how much money they had just spent. The amounts were [latex]{$0}[/latex] , [latex]{$14.95}[/latex] , [latex]{$35.25}[/latex] , and [latex]{$25.16}[/latex] . Find the mean amount of money spent.
   Show Solution

   $18.84
2. Juan bought [latex]5[/latex] shirts to wear to his new job. The costs of the shirts were [latex]{$32.95}[/latex] , [latex]{$38.50}[/latex] , [latex]{$30.00}[/latex] , [latex]{$17.45}[/latex] , and [latex]{$24.25}[/latex] . Find the mean cost.
3. The number of minutes it took Jim to ride his bike to school for each of the past six days was [latex]21[/latex] , [latex]18[/latex] , [latex]16[/latex] , [latex]19[/latex] , [latex]24[/latex] , and [latex]19[/latex] . Find the mean number of minutes.
   Show Solution

   19.5 minutes
4. Norris bought six books for his classes this semester. The costs of the books were [latex]{$74.28}[/latex] , [latex]{$120.95}[/latex] , [latex]{$52.40}[/latex] , [latex]{$10.59}[/latex] , [latex]{$35.89}[/latex] , and [latex]{$59.24}[/latex] . Find the mean cost.
5. The top eight hitters in a softball league have batting averages of [latex].373[/latex] , [latex].360[/latex] , [latex].321[/latex] , [latex].321[/latex] , [latex].320[/latex] , [latex].312[/latex] , [latex].311[/latex] , and [latex].311[/latex] . Find the mean of the batting averages. Round your answer to the nearest thousandth.
   Show Solution

   0.329
6. The monthly snowfall at a ski resort over a six-month period was [latex]60.3[/latex], [latex]79.7[/latex], [latex]50.9[/latex], [latex]28.0[/latex], [latex]47.4[/latex], and [latex]46.1[/latex] inches. Find the mean snowfall.

Find the Median of a Set of Numbers

In the following exercises, find the median.

1. [latex]24[/latex] , [latex]19[/latex] , [latex]18[/latex] , [latex]29[/latex] , [latex]21[/latex]
   Show Solution

   21
2. [latex]48[/latex] , [latex]51[/latex] , [latex]46[/latex] , [latex]42[/latex] , [latex]50[/latex]
3. [latex]65[/latex] , [latex]56[/latex] , [latex]35[/latex] , [latex]34[/latex] , [latex]44[/latex] , [latex]39[/latex] , [latex]55[/latex] , [latex]52[/latex] , [latex]45[/latex]
   Show Solution

   45
4. [latex]121[/latex] , [latex]115[/latex] , [latex]135[/latex] , [latex]109[/latex] , [latex]136[/latex] , [latex]147[/latex] , [latex]127[/latex] , [latex]119[/latex] , [latex]110[/latex]
5. [latex]4[/latex] , [latex]8[/latex] , [latex]1[/latex] , [latex]5[/latex] , [latex]14[/latex] , [latex]3[/latex] , [latex]1[/latex] , [latex]12[/latex]
   Show Solution

   4.5
6. [latex]3[/latex] , [latex]9[/latex] , [latex]2[/latex] , [latex]6[/latex] , [latex]20[/latex] , [latex]3[/latex] , [latex]3[/latex] , [latex]10[/latex]
7. [latex]99.2[/latex] , [latex]101.9[/latex] , [latex]98.6[/latex] , [latex]99.5[/latex] , [latex]100.8[/latex] , [latex]99.8[/latex]
   Show Solution

   99.65
8. [latex]28.8[/latex] , [latex]32.9[/latex] , [latex]32.5[/latex] , [latex]27.9[/latex] , [latex]30.4[/latex] , [latex]32.5[/latex] , [latex]31.6[/latex] , [latex]32.7[/latex]

Find the Median of a Set of Numbers in Applications

In the following exercises, find the median.

1. Last week Ray recorded how much he spent for lunch each workday. He spent [latex]{$6.50}[/latex] , [latex]{$7.25}[/latex] , [latex]{$4.90}[/latex] , [latex]{$5.30}[/latex] , and [latex]{$12.00}[/latex] . Find the median.
   Show Solution

   $6.50
2. Michaela is in charge of 6 two-year olds at a daycare center. Their ages, in months, are [latex]25[/latex] , [latex]24[/latex] , [latex]28[/latex] , [latex]32[/latex] , [latex]29[/latex] , and [latex]31[/latex] . Find the median age.
3. Brian is teaching a swim class for [latex]6[/latex] three-year olds. Their ages, in months, are [latex]38,41,45,36,40,\text{and}42[/latex]. Find the median age.
   Show Solution

   40.5 months
4. Sal recorded the amount he spent for gas each week for the past [latex]8[/latex] weeks. The amounts were [latex]{$38.65}[/latex], [latex]{$32.18}[/latex], [latex]{$40.23}[/latex], [latex]{$51.50}[/latex], [latex]{$43.68}[/latex], [latex]{$30.96}[/latex], [latex]{$41.37}[/latex], and [latex]{$44.72}[/latex]. Find the median amount.

Identify the Mode of a Set of Numbers

In the following exercises, identify the mode.

1. [latex]2[/latex] , [latex]5[/latex] , [latex]1[/latex] , [latex]5[/latex] , [latex]2[/latex] , [latex]1[/latex] , [latex]2[/latex] , [latex]3[/latex] , [latex]2[/latex] , [latex]3[/latex] , [latex]1[/latex]
   Show Solution

   2
2. [latex]8[/latex] , [latex]5[/latex] , [latex]1[/latex] , [latex]3[/latex] , [latex]7[/latex] , [latex]1[/latex] , [latex]1[/latex] , [latex]7[/latex] , [latex]1[/latex] , [latex]8[/latex] , [latex]7[/latex]
3. [latex]18[/latex] , [latex]22[/latex] , [latex]17[/latex] , [latex]20[/latex] , [latex]19[/latex] , [latex]20[/latex] , [latex]22[/latex] , [latex]19[/latex] , [latex]29[/latex] , [latex]18[/latex] , [latex]23[/latex] , [latex]25[/latex] , [latex]22[/latex] , [latex]24[/latex] , [latex]23[/latex] , [latex]22[/latex] , [latex]18[/latex] , [latex]20[/latex] , [latex]22[/latex] , [latex]20[/latex]
   Show Solution

   22
4. [latex]42[/latex] , [latex]28[/latex] , [latex]32[/latex] , [latex]35[/latex] , [latex]24[/latex] , [latex]32[/latex] , [latex]48[/latex] , [latex]32[/latex] , [latex]32[/latex] , [latex]24[/latex] , [latex]35[/latex] , [latex]28[/latex] , [latex]30[/latex] , [latex]35[/latex] , [latex]45[/latex] , [latex]32[/latex] , [latex]28[/latex] , [latex]32[/latex] , [latex]42[/latex] , [latex]42[/latex] , [latex]30[/latex]
5. The number of children per house on one block: [latex]1[/latex] , [latex]4[/latex] , [latex]2[/latex] , [latex]3[/latex] , [latex]3[/latex] , [latex]2[/latex] , [latex]6[/latex] , [latex]2[/latex] , [latex]4[/latex] , [latex]2[/latex] , [latex]0[/latex] , [latex]3[/latex] , [latex]0[/latex].
   Show Solution

   2 children
6. The number of movies watched each month last year: [latex]2[/latex] , [latex]0[/latex] , [latex]3[/latex] , [latex]0[/latex] , [latex]0[/latex] , [latex]8[/latex] , [latex]6[/latex] , [latex]5[/latex] , [latex]0[/latex] , [latex]1[/latex] , [latex]2[/latex] , [latex]3[/latex].
7. The number of units being taken by students in one class: [latex]12[/latex] , [latex]5[/latex] , [latex]11[/latex] , [latex]10[/latex] , [latex]10[/latex] , [latex]11[/latex] , [latex]5[/latex] , [latex]11[/latex] , [latex]11[/latex] , [latex]11[/latex] , [latex]10[/latex] , [latex]12[/latex] .
   Show Solution

   11 units
8. The number of hours of sleep per night for the past two weeks: [latex]8[/latex] , [latex]5[/latex] , [latex]7[/latex] , [latex]8[/latex] , [latex]8[/latex] ,
9. [latex]6[/latex] , [latex]6[/latex] , [latex]6[/latex] , [latex]6[/latex] , [latex]9[/latex] , [latex]7[/latex] , [latex]8[/latex] , [latex]8[/latex] , [latex]8[/latex] .

Use the Basic Definition of Probability

In the following exercises, express the probability as both a fraction and a decimal. (Round to three decimal places, if necessary.)

1. Josue is in a book club with [latex]20[/latex] members. One member is chosen at random each month to select the next month’s book. Find the probability that Josue will be chosen next month.
   Show Solution

   [latex]\Large\frac{1}{20}\normalsize,0.05[/latex]
2. Jessica is one of eight kindergarten teachers at Mandela Elementary School. One of the kindergarten teachers will be selected at random to attend a summer workshop. Find the probability that Jessica will be selected.
3. There are [latex]24[/latex] people who work in Dane’s department. Next week, one person will be selected at random to bring in doughnuts. Find the probability that Dane will be selected. Round your answer to the nearest thousandth.
   Show Solution

   [latex]\Large\frac{1}{24}\normalsize,0.041\stackrel{-}{6}\approx 0.042[/latex]
4. Monica has two strawberry yogurts and six banana yogurts in her refrigerator. She will choose one yogurt at random to take to work. Find the probability Monica will choose a strawberry yogurt.
5. Michel has four rock CDs and six country CDs in his car. He will pick one CD to play on his way to work. Find the probability Michel will pick a rock CD.
   Show Solution

   [latex]\Large\frac{4}{10}\normalsize,0.4[/latex]
6. Noah is planning his summer camping trip. He can’t decide among six campgrounds at the beach and twelve campgrounds in the mountains, so he will choose one campground at random. Find the probability that Noah will choose a campground at the beach.
7. Donovan is considering transferring to a [latex]\text{4-year college}[/latex]. He is considering [latex]10[/latex] out-of state colleges and [latex]4[/latex] colleges in his state. He will choose one college at random to visit during spring break. Find the probability that Donovan will choose an out-of-state college.
   Show Solution

   [latex]\Large\frac{10}{14}\normalsize,0.\stackrel{\text{—}}{714285}\approx 0.714[/latex]
8. There are [latex]258,890,850[/latex] number combinations possible in the Mega Millions lottery. One winning jackpot ticket will be chosen at random. Brent chooses his favorite number combination and buys one ticket. Find the probability Brent will win the jackpot. Round the decimal to the first digit that is not zero, then write the name of the decimal.

Write a Ratio as a Fraction

In the following exercises, write each ratio as a fraction.

1. [latex]20[/latex] to [latex]36[/latex]
   Show Solution

   [latex]\Large\frac{5}{9}[/latex]
2. [latex]20[/latex] to [latex]32[/latex]
3. [latex]42[/latex] to [latex]48[/latex]
   Show Solution

   [latex]\Large\frac{7}{8}[/latex]
4. [latex]45[/latex] to [latex]54[/latex]
5. [latex]49[/latex] to [latex]21[/latex]
   Show Solution

   [latex]\Large\frac{7}{3}[/latex]
6. [latex]56[/latex] to [latex]16[/latex]
7. [latex]84[/latex] to [latex]36[/latex]
   Show Solution

   [latex]\Large\frac{7}{3}[/latex]
8. [latex]6.4[/latex] to [latex]0.8[/latex]
9. [latex]0.56[/latex] to [latex]2.8[/latex]
   Show Solution

   [latex]\Large\frac{1}{5}[/latex]
10. [latex]1.26[/latex] to [latex]4.2[/latex]
11. [latex]1\Large\frac{2}{3}[/latex] to [latex]2\Large\frac{5}{6}[/latex]
    Show Solution

    [latex]\Large\frac{10}{17}[/latex]
12. [latex]1\Large\frac{3}{4}[/latex] to [latex]2\Large\frac{5}{8}[/latex]
13. [latex]4\Large\frac{1}{6}[/latex] to [latex]3\Large\frac{1}{3}[/latex]
    Show Solution

    [latex]\Large\frac{5}{4}[/latex]
14. [latex]5\Large\frac{3}{5}[/latex] to [latex]3\Large\frac{3}{5}[/latex]
15. [latex]{$18}[/latex] to [latex]{$63}[/latex]
    Show Solution

    [latex]\Large\frac{2}{7}[/latex]
16. [latex]{$16}[/latex] to [latex]{$72}[/latex]
17. [latex]{$1.21}[/latex] to [latex]{$0.44}[/latex]
    Show Solution

    [latex]\Large\frac{11}{4}[/latex]
18. [latex]{$1.38}[/latex] to [latex]{$0.69}[/latex]
19. [latex]28[/latex] ounces to [latex]84[/latex] ounces
    Show Solution

    [latex]\Large\frac{1}{3}[/latex]
20. [latex]32[/latex] ounces to [latex]128[/latex] ounces
21. [latex]12[/latex] feet to [latex]46[/latex] feet
    Show Solution

    [latex]\Large\frac{6}{23}[/latex]
22. [latex]15[/latex] feet to [latex]57[/latex] feet
23. [latex]246[/latex] milligrams to [latex]45[/latex] milligrams
    Show Solution

    [latex]\Large\frac{82}{15}[/latex]
24. [latex]304[/latex] milligrams to [latex]48[/latex] milligrams
25. total cholesterol of [latex]175[/latex] to HDL cholesterol of [latex]45[/latex]
    Show Solution

    [latex]\Large\frac{35}{9}[/latex]
26. total cholesterol of [latex]215[/latex] to HDL cholesterol of [latex]55[/latex]
27. [latex]27[/latex] inches to [latex]1[/latex] foot
    Show Solution

    [latex]\Large\frac{9}{4}[/latex]
28. [latex]28[/latex] inches to [latex]1[/latex] foot

Write a Rate as a Fraction

In the following exercises, write each rate as a fraction.

1. [latex]140[/latex] calories per [latex]12[/latex] ounces
   Show Solution

   [latex]\Large\frac{\text{35 calories}}{\text{3 ounces}}[/latex]
2. [latex]180[/latex] calories per [latex]16[/latex] ounces
3. [latex]8.2[/latex] pounds per [latex]3[/latex] square inches
   Show Solution

   [latex]\Large\frac{\text{41 lbs}}{\text{15 sq. in}.}[/latex]
4. [latex]9.5[/latex] pounds per [latex]4[/latex] square inches
5. [latex]488[/latex] miles in [latex]7[/latex] hours
   Show Solution

   [latex]\Large\frac{\text{488 miles}}{\text{7 hours}}[/latex]
6. [latex]527[/latex] miles in [latex]9[/latex] hours
7. [latex]{$595}[/latex] for [latex]40[/latex] hours
   Show Solution

   [latex]\Large\frac{{$119}}{{8 hours}}[/latex]
8. [latex]{$798}[/latex] for [latex]40[/latex] hours

Find Unit Rates

Exercise 1

In the following exercises, find the unit rate. Round to two decimal places, if necessary.

1. [latex]140[/latex] calories per [latex]12[/latex] ounces
   Show Solution

   11.67 calories/ounce
2. [latex]180[/latex] calories per [latex]16[/latex] ounces
3. [latex]8.2[/latex] pounds per [latex]3[/latex] square inches
   Show Solution

   2.73 lbs./sq. in.
4. [latex]9.5[/latex] pounds per [latex]4[/latex] square inches
5. [latex]488[/latex] miles in [latex]7[/latex] hours
   Show Solution

   69.71 mph
6. [latex]527[/latex] miles in [latex]9[/latex] hours
7. [latex]{$595}[/latex] for [latex]40[/latex] hours
   Show Solution

   $14.88/hour
8. [latex]{$798}[/latex] for [latex]40[/latex] hours
9. [latex]576[/latex] miles on [latex]18[/latex] gallons of gas
   Show Solution

   32 mpg
10. [latex]435[/latex] miles on [latex]15[/latex] gallons of gas
11. [latex]43[/latex] pounds in [latex]16[/latex] weeks
    Show Solution

    2.69 lbs./week
12. [latex]57[/latex] pounds in [latex]24[/latex] weeks
13. [latex]46[/latex] beats in [latex]0.5[/latex] minute
    Show Solution

    92 beats/minute
14. [latex]54[/latex] beats in [latex]0.5[/latex] minute

Exercise 2

1. The bindery at a printing plant assembles [latex]96,000[/latex] magazines in [latex]12[/latex] hours. How many magazines are assembled in one hour?
   Show Solution

   8,000
2. The pressroom at a printing plant prints [latex]540,000[/latex] sections in [latex]12[/latex] hours. How many sections are printed per hour?

Find Unit Price

Exercise 1

In the following exercises, find the unit price. Round to the nearest cent.

1. Soap bars at [latex]8[/latex] for [latex]{$8.69}[/latex]
   Show Solution

   $1.09/bar
2. Soap bars at [latex]4[/latex] for [latex]{$3.39}[/latex]
3. Women’s sports socks at [latex]6[/latex] pairs for [latex]{$7.99}[/latex]
   Show Solution

   $1.33/pair
4. Men’s dress socks at [latex]3[/latex] pairs for [latex]{$8.49}[/latex]
5. Snack packs of cookies at [latex]12[/latex] for [latex]{$5.79}[/latex]
   Show Solution

   $0.48/pack
6. Granola bars at [latex]5[/latex] for [latex]{$3.69}[/latex]
7. CD-RW discs at [latex]25[/latex] for [latex]{$14.99}[/latex]
   Show Solution

   $0.60/disc
8. CDs at [latex]50[/latex] for [latex]{$4.49}[/latex]

Exercise 2

1. The grocery store has a special on macaroni and cheese. The price is [latex]{$3.87}[/latex] for [latex]3[/latex] boxes. How much does each box cost?
   Show Solution

   $1.29/box
2. The pet store has a special on cat food. The price is [latex]{$4.32}[/latex] for [latex]12[/latex] cans. How much does each can cost?

Find Unit Price

In the following exercises, find each unit price and then identify the better buy. Round to three decimal places.

1. Mouthwash, [latex]{50.7-ounce}[/latex] size for [latex]{$6.99}[/latex] or [latex]{33.8-ounce}[/latex] size for [latex]{$4.79}[/latex]
   Show Solution

   The 50.7-ounce size costs $0.138 per ounce. The 33.8-ounce size costs $0.142 per ounce. The 50.7-ounce size is the better buy.
2. Toothpaste, [latex]6[/latex] ounce size for [latex]{$3.19}[/latex] or [latex]7.8-ounce[/latex] size for [latex]{$5.19}[/latex]
3. Breakfast cereal, [latex]18[/latex] ounces for [latex]{$3.99}[/latex] or [latex]14[/latex] ounces for [latex]{$3.29}[/latex]
   Show Solution

   The 18-ounce size costs $0.222 per ounce. The 14-ounce size costs $0.235 per ounce. The 18-ounce size is a better buy.
4. Breakfast Cereal, [latex]10.7[/latex] ounces for [latex]{$2.69}[/latex] or [latex]14.8[/latex] ounces for [latex]{$3.69}[/latex]
5. Ketchup, [latex]{40-ounce}[/latex] regular bottle for [latex]{$2.99}[/latex] or [latex]{64-ounce}[/latex] squeeze bottle for [latex]{$4.39}[/latex]
   Show Solution

   The regular bottle costs $0.075 per ounce. The squeeze bottle costs $0.069 per ounce. The squeeze bottle is a better buy.
6. Mayonnaise [latex]{15-ounce}[/latex] regular bottle for [latex]{$3.49}[/latex] or [latex]{22-ounce}[/latex] squeeze bottle for [latex]{$4.99}[/latex]
7. Cheese [latex]{$6.49}[/latex] for [latex]1[/latex] lb. block or [latex]{$3.39}[/latex] for [latex]\Large\frac{1}{2}[/latex] lb. block
   Show Solution

   The half-pound block costs $6.78/lb, so the 1-lb. block is a better buy.
8. Candy [latex]{$10.99}[/latex] for a [latex]1[/latex] lb. bag or [latex]{$2.89}[/latex] for [latex]\Large\frac{1}{4}[/latex] lb. of loose candy

Translate Phrases to Expressions with Fractions

In the following exercises, translate the English phrase into an algebraic expression.

1. [latex]793[/latex] miles per [latex]p[/latex] hours
   Show Solution

   [latex]\Large\frac{\text{793 miles}}{p \text{hours}}[/latex]
2. [latex]78[/latex] feet per [latex]r[/latex] seconds
3. [latex]{$3}[/latex] for [latex]0.5[/latex] lbs.
   Show Solution

   [latex]\Large\frac{{$3}}{{0.5 lbs}.}[/latex]
4. [latex]j[/latex] beats in [latex]0.5[/latex] minutes
5. [latex]105[/latex] calories in [latex]x[/latex] ounces
   Show Solution

   [latex]\Large\frac{\text{105 calories}} {x \text {ounces}}[/latex]
6. [latex]400[/latex] minutes for [latex]m[/latex] dollars
7. the ratio of [latex]y[/latex] and [latex]5x[/latex]
   Show Solution

   [latex]\Large\frac{y}{5x}[/latex]
8. the ratio of [latex]12x[/latex] and [latex]y[/latex]

Everyday Math

 

 

Simplify Expressions with Square Roots

In the following exercises, simplify.

1. [latex]\sqrt{36}[/latex]
   Show Solution

   6
2. [latex]\sqrt{4}[/latex]
3. [latex]\sqrt{64}[/latex]
   Show Solution

   8
4. [latex]\sqrt{144}[/latex]
5. [latex]-\sqrt{4}[/latex]
   Show Solution

   −2
6. [latex]-\sqrt{100}[/latex]
7. [latex]-\sqrt{1}[/latex]
   Show Solution

   −1
8. [latex]-\sqrt{121}[/latex]
9. [latex]\sqrt{-121}[/latex]
   Show Solution

   not a real number
10. [latex]\sqrt{-36}[/latex]
11. [latex]\sqrt{-9}[/latex]
    Show Solution

    not a real number
12. [latex]\sqrt{-49}[/latex]
13. [latex]\sqrt{9+16}[/latex]
    Show Solution

    5
14. [latex]\sqrt{25+144}[/latex]
15. [latex]\sqrt{9}+\sqrt{16}[/latex]
    Show Solution

    7
16. [latex]\sqrt{25}+\sqrt{144}[/latex]

Estimate Square Roots

In the following exercises, estimate each square root between two consecutive whole numbers.

1. [latex]\sqrt{70}[/latex]
   Show Solution

   [latex]8<\sqrt{70}<9[/latex]
2. [latex]\sqrt{55}[/latex]
3. [latex]\sqrt{200}[/latex]
   Show Solution

   [latex]14<\sqrt{200}<15[/latex]
4. [latex]\sqrt{172}[/latex]

Approximate Square Roots with a Calculator

In the following exercises, use a calculator to approximate each square root and round to two decimal places.

1. [latex]\sqrt{19}[/latex]
   Show Solution

   4.36
2. [latex]\sqrt{21}[/latex]
3. [latex]\sqrt{53}[/latex]
   Show Solution

   7.28
4. [latex]\sqrt{47}[/latex]

Simplify Variable Expressions with Square Roots

In the following exercises, simplify. (Assume all variables are greater than or equal to zero.)

1. [latex]\sqrt{{y}^{2}}[/latex]
   Show Solution

   y
2. [latex]\sqrt{{b}^{2}}[/latex]
3. [latex]\sqrt{49{x}^{2}}[/latex]
   Show Solution

   7x
4. [latex]\sqrt{100{y}^{2}}[/latex]
5. [latex]-\sqrt{64{a}^{2}}[/latex]
   Show Solution

   −8a
6. [latex]-\sqrt{25{x}^{2}}[/latex]
7. [latex]\sqrt{144{x}^{2}{y}^{2}}[/latex]
   Show Solution

   12xy
8. [latex]\sqrt{196{a}^{2}{b}^{2}}[/latex]

Use Square Roots in Applications

In the following exercises, solve. Round to one decimal place.

Landscaping Reed wants to have a square garden plot in his backyard. He has enough compost to cover an area of [latex]75[/latex] square feet. How long can a side of his garden be?

Landscaping Vince wants to make a square patio in his yard. He has enough concrete to pave an area of [latex]130[/latex] square feet. How long can a side of his patio be?

Gravity An airplane dropped a flare from a height of [latex]1,024[/latex] feet above a lake. How many seconds did it take for the flare to reach the water?

Gravity A hang glider dropped his cell phone from a height of [latex]350[/latex] feet. How many seconds did it take for the cell phone to reach the ground?

Gravity A construction worker dropped a hammer while building the Grand Canyon skywalk, [latex]4,000[/latex] feet above the Colorado River. How many seconds did it take for the hammer to reach the river?

Accident investigation The skid marks from a car involved in an accident measured [latex]54[/latex] feet. What was the speed of the car before the brakes were applied?

Accident investigation The skid marks from a car involved in an accident measured [latex]216[/latex] feet. What was the speed of the car before the brakes were applied?

Accident investigation An accident investigator measured the skid marks of one of the vehicles involved in an accident. The length of the skid marks was [latex]175[/latex] feet. What was the speed of the vehicle before the brakes were applied?

Accident investigation An accident investigator measured the skid marks of one of the vehicles involved in an accident. The length of the skid marks was [latex]117[/latex] feet. What was the speed of the vehicle before the brakes were applied?

 

Chapter Review Exercises

Decimals

Name Decimals

In the following exercises, name each decimal.

1. [latex]0.8[/latex]
2. [latex]0.375[/latex]
   Show Solution

   three hundred seventy-five thousandths
3. [latex]0.007[/latex]
4. [latex]5.24[/latex]
   Show Solution

   five and twenty-four hundredths
5. [latex]-12.5632[/latex]
6. [latex]-4.09[/latex]
   Show Solution

   negative four and nine hundredths

Write Decimals
In the following exercises, write as a decimal.

1. three tenths
2. nine hundredths
   Show Solution

   0.09
3. twenty-seven hundredths
4. ten and thirty-five thousandths
   Show Solution

   10.035
5. negative twenty and three tenths
6. negative five hundredths
   Show Solution

   −0.05

Convert Decimals to Fractions or Mixed Numbers

In the following exercises, convert each decimal to a fraction. Simplify the answer if possible.

1. [latex]0.43[/latex]
2. [latex]0.825[/latex]
   Show Solution

   [latex]\Large\frac{33}{40}[/latex]
3. [latex]9.7[/latex]
4. [latex]3.64[/latex]
   Show Solution

   [latex]3\Large\frac{16}{25}[/latex]

Locate Decimals on the Number Line

1. [latex]0.6[/latex]
2. [latex]-0.9[/latex]
3. [latex]2.2[/latex]
4. [latex]-1.3[/latex]

Order Decimals
In the following exercises, order each of the following pairs of numbers, using [latex]<[/latex]; or [latex]\text{>.}[/latex]

1. [latex]0.6\text{___}0.8[/latex]
   Show Solution

   <
2. [latex]0.2\text{___}0.15[/latex]
3. [latex]0.803\text{____}0.83[/latex]
   Show Solution

   <
4. [latex]-0.56\text{____} - 0.562[/latex]

Round Decimals
In the following exercises, round each number to the nearest: ⓐ hundredth ⓑ tenth ⓒ whole number.

1. [latex]12.529[/latex]
   Show Solution

   ⓐ 12.53 ⓑ 12.5 ⓒ 13
2. [latex]4.8447[/latex]
3. [latex]5.897[/latex]
   Show Solution

   ⓐ 5.90 ⓑ 5.9 ⓒ 6

Decimal Operations

Add and Subtract Decimals
In the following exercises, add or subtract.

1. [latex]5.75+8.46[/latex]
2. [latex]32.89 - 8.22[/latex]
   Show Solution

   24.67
3. [latex]24 - 19.31[/latex]
4. [latex]10.2+14.631[/latex]
   Show Solution

   24.831
5. [latex]-6.4+\left(-2.9\right)[/latex]
6. [latex]1.83 - 4.2[/latex]
   Show Solution

   −2.37

Multiply Decimals

In the following exercises, multiply.

1. [latex]\left(0.3\right)\left(0.7\right)[/latex]
2. [latex]\left(-6.4\right)\left(0.25\right)[/latex]
   Show Solution

   −1.6
3. [latex]\left(-3.35\right)\left(-12.7\right)[/latex]
4. [latex]\left(15.4\right)\left(1000\right)[/latex]
   Show Solution

   15,400

Divide Decimals

In the following exercises, divide.

1. [latex]0.48\div 6[/latex]
2. [latex]4.32\div 24[/latex]
   Show Solution

   0.18
3. [latex]{$6.29}\div 12[/latex]
4. [latex]\left(-0.8\right)\div \left(-0.2\right)[/latex]
   Show Solution

   4
5. [latex]1.65\div 0.15[/latex]
6. [latex]9\div 0.045[/latex]
   Show Solution

   200

Use Decimals in Money Applications

In the following exercises, use the strategy for applications to solve.

1. Miranda got [latex]{$40}[/latex] from her ATM. She spent [latex]{$9.32}[/latex] on lunch and [latex]{$16.99}[/latex] on a book. How much money did she have left? Round to the nearest cent if necessary.
2. Jessie put [latex]8[/latex] gallons of gas in her car. One gallon of gas costs [latex]{$3.528.}[/latex] How much did Jessie owe for all the gas?
   Show Solution

   $28.22
3. A pack of [latex]16[/latex] water bottles cost [latex]{$6.72.}[/latex] How much did each bottle cost?
4. Alice bought a roll of paper towels that cost [latex]{$2.49.}[/latex] She had a coupon for [latex]{$0.35}[/latex] off, and the store doubled the coupon. How much did Alice pay for the paper towels?
   Show Solution

   $1.79

Decimals and Fractions

Convert Fractions to Decimals
In the following exercises, convert each fraction to a decimal.

1. [latex]\Large\frac{3}{5}[/latex]
2. [latex]\Large\frac{7}{8}[/latex]
   Show Solution

   0.875
3. [latex]-\Large\frac{19}{20}[/latex]
4. [latex]-\Large\frac{21}{4}[/latex]
   Show Solution

   −5.25
5. [latex]\Large\frac{1}{3}[/latex]
6. [latex]\Large\frac{6}{11}[/latex]
   Show Solution

   [latex]0.\stackrel{\text{-}}{54}[/latex]

Order Decimals and Fractions

In the following exercises, order each pair of numbers, using [latex]<[/latex]; or [latex]\text{>.}[/latex]

1. [latex]\Large\frac{1}{2}\text{___}\normalsize 0.2[/latex]
2. [latex]\Large\frac{3}{5}\text{___}\normalsize 0[/latex].
   Show Solution

   >
3. [latex]-\Large\frac{7}{8}\text{___}\normalsize - 0.84[/latex]
4. [latex]-\Large\frac{5}{12}\text{___}\normalsize - 0.42[/latex]
   Show Solution

   >
5. [latex]0.625\text{___}\Large\frac{13}{20}[/latex]
6. [latex]0.33\text{___}\Large\frac{5}{16}[/latex]
   Show Solution

   >

In the following exercises, write each set of numbers in order from least to greatest.

1. [latex]\Large\frac{2}{3}\normalsize ,\Large\frac{17}{20}\normalsize ,0.65[/latex]
2. [latex]\Large\frac{7}{9}\normalsize ,0.75\normalsize ,\Large\frac{11}{15}[/latex]
   Show Solution

   [latex]\Large\frac{11}{15}\normalsize ,0.75,\Large\frac{7}{9}[/latex]

Simplify Expressions Using the Order of Operations
In the following exercises, simplify

1. [latex]4\left(10.3 - 5.8\right)[/latex]
2. [latex]\Large\frac{3}{4}\normalsize\left(15.44 - 7.4\right)[/latex]
   Show Solution

   6.03
3. [latex]30\div \left(0.45+0.15\right)[/latex]
4. [latex]1.6+\Large\frac{3}{8}[/latex]
   Show Solution

   1.975
5. [latex]52\left(0.5\right)+{\left(0.4\right)}^{2}[/latex]
6. [latex]-\Large\frac{2}{5}\normalsize\cdot\Large\frac{9}{10}\normalsize +0.14[/latex]
   Show Solution

   −0.22

Find the Circumference and Area of Circles

In the following exercises, approximate the ⓐ circumference and ⓑ area of each circle.

1. [latex]\text{radius}=\text{6 in.}[/latex]
2. [latex]\text{radius}=\text{3.5 ft.}[/latex]
   Show Solution

   ⓐ 21.98 ft. ⓑ 38.465 sq.ft.
3. [latex]\text{radius}=\Large\frac{7}{33}\normalsize\text{m}[/latex]
4. [latex]\text{diameter}=\text{11 cm}[/latex]
   Show Solution

   ⓐ 34.54 cm ⓑ 379.94 sq.cm

Solving Equations With Decimals

Determine Whether a Decimal is a Solution of an Equation
In the following exercises, determine whether each number is a solution of the given equation.

[latex]x - 0.8=2.3[/latex]

ⓐ [latex]x=2[/latex] ⓑ [latex]x=-1.5[/latex] ⓒ [latex]x=3.1[/latex]

[latex]y+0.6=-3.4[/latex]

ⓐ [latex]y=-4[/latex] ⓑ [latex]y=-2.8[/latex] ⓒ [latex]y=2.6[/latex]

[latex]\Large\frac{h}{1.5}\normalsize =-4.3[/latex]

ⓐ [latex]h=6.45[/latex] ⓑ [latex]h=-6.45[/latex] ⓒ [latex]h=-2.1[/latex]

[latex]0.75k=-3.6[/latex]

ⓐ [latex]k=-0.48[/latex] ⓑ [latex]k=-4.8[/latex] ⓒ [latex]k=-2.7[/latex]

Solve Equations with Decimals

In the following exercises, solve the equation.

1. [latex]y+2.9=5.7[/latex]
   Show Solution

   y = 2.8

2. [latex]m+4.6=6.5[/latex]
3. [latex]f+3.45=2.6[/latex]
   Show Solution

   f = −0.85
4. [latex]h+4.37=3.5[/latex]
5. [latex]a+6.2=-1.7[/latex]
   Show Solution

   a = −7.9
6. [latex]b+5.8=-2.3[/latex]
7. [latex]c+1.15=-3.5[/latex]
   Show Solution

   c = −4.65
8. [latex]d+2.35=-4.8[/latex]
9. [latex]n - 2.6=1.8[/latex]
   Show Solution

   n = 4.4
10. [latex]p - 3.6=1.7[/latex]
11. [latex]x - 0.4=-3.9[/latex]
    Show Solution

    x = −3.5
12. [latex]y - 0.6=-4.5[/latex]
13. [latex]j - 1.82=-6.5[/latex]
    Show Solution

    j = −4.68
14. [latex]k - 3.19=-4.6[/latex]
15. [latex]m - 0.25=-1.67[/latex]
    Show Solution

    m = −1.42
16. [latex]q - 0.47=-1.53[/latex]
17. [latex]0.5x=3.5[/latex]
    Show Solution

    x = 7
18. [latex]0.4p=9.2[/latex]
19. [latex]-1.7c=8.5[/latex]
    Show Solution

    c = −5
20. [latex]-2.9x=5.8[/latex]
21. [latex]-1.4p=-4.2[/latex]
    Show Solution

    p = 3
22. [latex]-2.8m=-8.4[/latex]
23. [latex]-120=1.5q[/latex]
    Show Solution

    q = −80
24. [latex]-75=1.5y[/latex]
25. [latex]0.24x=4.8[/latex]
    Show Solution

    x = 20
26. [latex]0.18n=5.4[/latex]
27. [latex]-3.4z=-9.18[/latex]
    Show Solution

    z = 2.7
28. [latex]-2.7u=-9.72[/latex]
29. [latex]\Large\frac{a}{0.4}\normalsize =-20[/latex]
    Show Solution

    a = −8
30. [latex]\Large\frac{b}{0.3}\normalsize =-9[/latex]
31. [latex]\Large\frac{x}{0.7}\normalsize =-0.4[/latex]
    Show Solution

    x = −0.28
32. [latex]\Large\frac{y}{0.8}\normalsize =-0.7[/latex]
33. [latex]\Large\frac{p}{-5}\normalsize =-1.65[/latex]
    Show Solution

    p = 8.25
34. [latex]\Large\frac{q}{-4}\normalsize =-5.92[/latex]
35. [latex]\Large\frac{r}{-1.2}\normalsize =-6[/latex]
    Show Solution

    r = 7.2
36. [latex]\Large\frac{s}{-1.5}\normalsize =-3[/latex]

Mixed Practice

In the following exercises, solve the equation. Then check your solution.

1. [latex]x - 5=-11[/latex]
   Show Solution

   x = −6

2. [latex]-\Large\frac{2}{5}\normalsize =x+\Large\frac{3}{4}[/latex]
3. [latex]p+8=-2[/latex]
   Show Solution

   p = −10
4. [latex]p+\Large\frac{2}{3}\normalsize =\Large\frac{1}{12}[/latex]
5. [latex]-4.2m=-33.6[/latex]
   Show Solution

   m = 8
6. [latex]q+9.5=-14[/latex]
7. [latex]q+\Large\frac{5}{6}\normalsize =\Large\frac{1}{12}[/latex]
   Show Solution